快速排序--QuickSort()--递归版本

一、快速排序（递归版本）

1.快速排序模板（初始版本）

void QuickSort(int* a, int begin, int end)
{
	// 区间不存在，或者只有一个值则不需要在处理
	if (begin >= end)
	{
		return;
	}
 
	int keyi = PartSort1(a, begin, end);
	
	// [begin, keyi-1] keyi [keyi+1, end]
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi+1, end);
}

存在问题、特点:

1.递归次数过多

2.有序等的极端情况会使其递归过深，导致栈溢出

3.没优化前,快排的效率和key的选取有关，选越靠近最大，或者越靠近最小的数，效率越慢；越靠近中位数，效率越快。

2.快速排序模板（优化版本）

void QuickSort(int* a, int begin, int end)
{
	//callCount++;
	//printf("%p\n", &callCount);
 
	// 区间不存在，或者只有一个值则不需要在处理
	if (begin >= end)
	{
		return;
	}
 
	if (end - begin > 10)
	{
		int keyi = PartSort1(a, begin, end);
		// [begin, keyi-1] keyi [keyi+1, end]
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}
	else
	{
		InsertSort(a+begin, end - begin + 1);//当区间过小时，可以直接用插入排序，较为高效
	}
}

图示:

优点:

假设总共有n个元素需要排的话，递归层次越深，所需要排序的次数也就越多，例:第一次要排两次，第二次要排四次，...,最后一次要2^h次，---(.h从0开始，树有h-1层，则树的总节点数为 n=2^(h+1) -1.得h=log(n+1) -1)---能看得出最后一次就占了全部排序次数的50%。 所以该优化方法，可以大大的减少排序的次数和递归的次数。

3.快速排序的三个方法partsort()

(1)hoare版本        时间复杂度:O(N*logN)

int PartSort1(int* a, int begin, int end)
{
	int left = begin, right = end;
	int keyi = left;
	while (left < right)
	{
		// 右边先走，找小
		while (left < right && a[right] >= a[keyi])
		{
			--right;
		}
 
		// 左边再走，找大
		while (left < right && a[left] <= a[keyi])
		{
			++left;
		}
 
		Swap(&a[left], &a[right]);
	}
 
	Swap(&a[keyi], &a[left]);
	keyi = left;
 
	return keyi;
}

(2)挖洞法

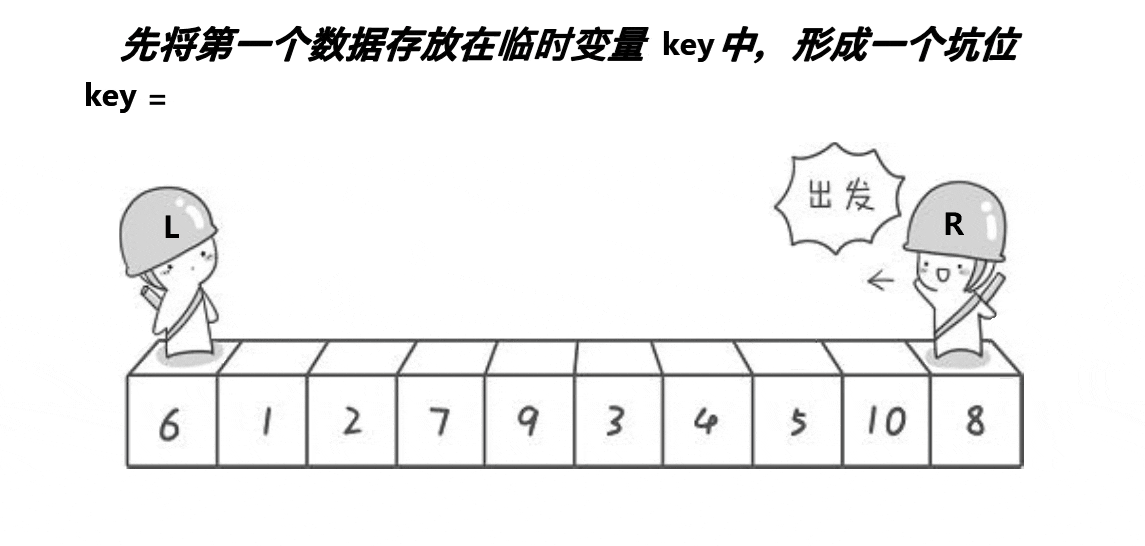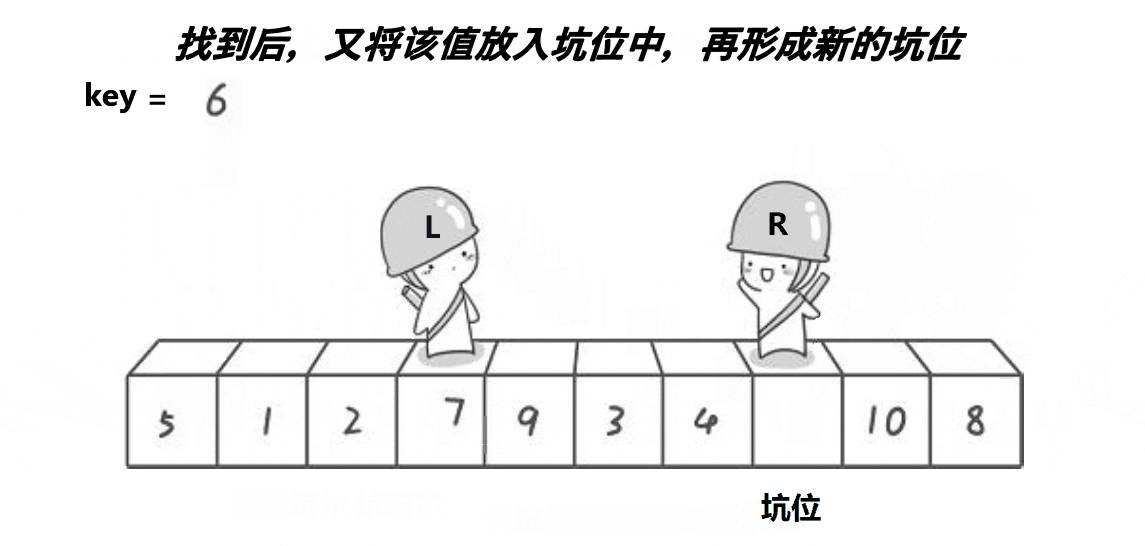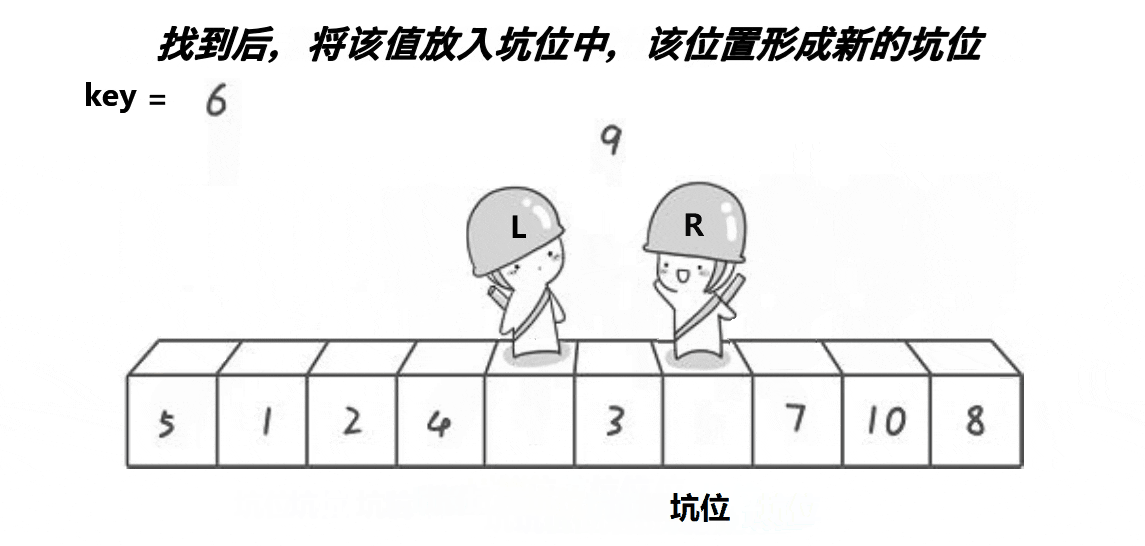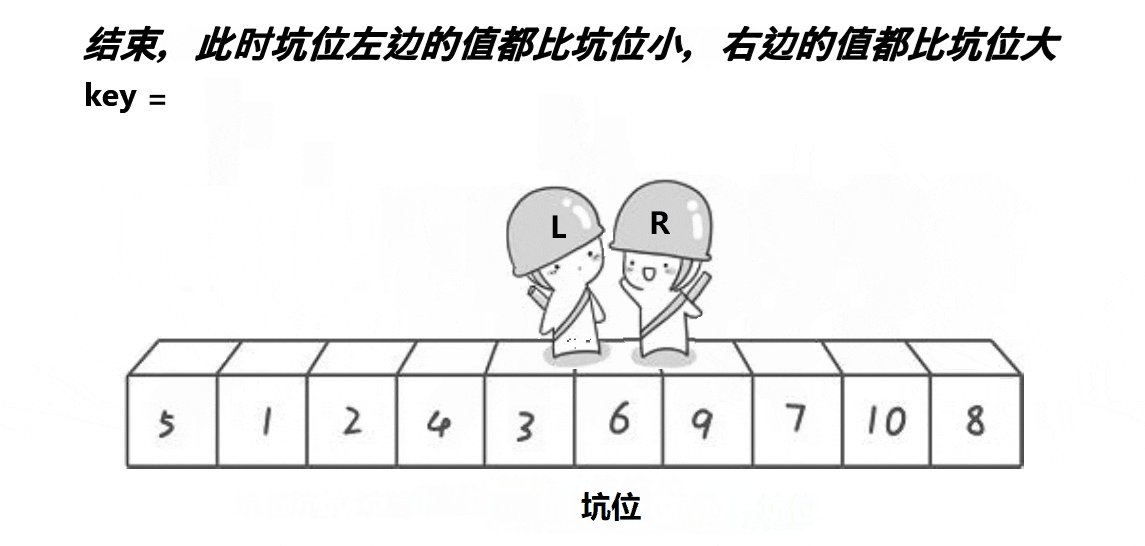
int PartSort2(int* a, int begin, int end)
{
	int key = a[begin];
	int piti = begin;
	while (begin < end)
	{
		// 右边找小，填到左边的坑里面去。这个位置形成新的坑
		while (begin < end && a[end] >= key)
		{
			--end;
		}
 
		a[piti] = a[end];
		piti = end;
 
		// 左边找大，填到右边的坑里面去。这个位置形成新的坑
		while (begin < end && a[begin] <= key)
		{
			++begin;
		}
 
		a[piti] = a[begin];
		piti = begin;
	}
 
	a[piti] = key;
	return piti;
}

(3)前后指针法 (进一步优化了模板--加入了getmid三数取中原则--减少了对有序序列排序时递归过深等的极端情况)

 

int GetMidIndex(int* a, int begin, int end)
{
	int mid = (begin + end) / 2;
	if (a[begin] < a[mid])
	{
		if (a[mid] < a[end])
		{
			return mid;
		}
		else if (a[begin] < a[end])
		{
			return end;
		}
		else
		{
			return begin;
		}
	}
	else if(a[begin] >= a[mid])
	{
		if (a[mid] > a[end])
		{
			return mid;
		}
		else if (a[begin] < a[end])
		{
			return begin;
		}
		else
		{
			return end;
		}
	}
}
 
 
 
int PartSort3(int* a, int begin, int end)
{
	int prev = begin;
	int cur = begin + 1;
	int keyi = begin;
 
	// 加入三数取中的优化--用于随机选midi放到keyi，使keyi既不是最大也不是最小
	int midi = GetMidIndex(a, begin, end);
	Swap(&a[keyi], &a[midi]);
 
	while (cur <= end)
	{
		// cur位置的之小于keyi位置值
		if (a[cur] < a[keyi] && ++prev != cur)
			Swap(&a[prev], &a[cur]);
 
		++cur;
	}
 
	Swap(&a[prev], &a[keyi]);
	keyi = prev;
 
	return keyi;
}

 4.疑惑解答

（1）hoare法 和 挖洞法 为什么 左边做key 一定要右边先走？

答:

1.R先走,R停下来，L去遇到R

可以保证:相遇位置就是R停下的位置，R的位置是比key要小的，确保后续和key交换时，是小的交换去左边了，大的在右边.

2.R先走，若R没有找到比key要小的值，R直接去到L

可以保证:相遇位置是L上一轮停下来的位置(要么就是key,要么就是比key要小的值。)

也确保了用R遇到的交换到左边的是key或者比key大的值.L交换到右边的是key或者比key要小的值

结论:左边做key，右边先走;右边做key，左边先走。