【LeetCode】Day128-合并K个升序链表

题目

23. 合并K个升序链表【困难】

题解

之前做过的合并两个升序链表，基本上已经可以熟读背诵，那么这道题的K个升序链表该怎么做呢？

顺序合并

最简单的方法，把K个链表合并转换成顺序两两合并，用res维护新链表，第 i 次循环将第 i 个链表和res合并。

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        int n=lists.length;
        if(n==0)
            return null;
        ListNode res=lists[0];
        for(int i=1;i<n;i++)
            res=merge2Lists(res,lists[i]);
        return res;
    }
    //合并两个有序链表
    public ListNode merge2Lists(ListNode res,ListNode node){
        ListNode head=new ListNode();
        ListNode p=res,q=node,tail=head;
        while(p!=null&&q!=null){
            if(p.val<q.val){
                tail.next=p;
                p=p.next;
            }
            else{
                tail.next=q;
                q=q.next;
            }
            tail=tail.next;
        }
        tail.next=p!=null?p:q;//剩余的非空链
        return head.next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

时间复杂度：$O(k^{2}n)$，假设每个链表的最长长度是n，那么第 i 次合并之后链表最长为i*n，第 i 次合并的时间复杂度是O($i\ast n$)，所以总时间复杂度为$O(((1+k)\ast k/2)\ast n)$，即为$O(k^{2}n)$

空间复杂度：$O(1)$

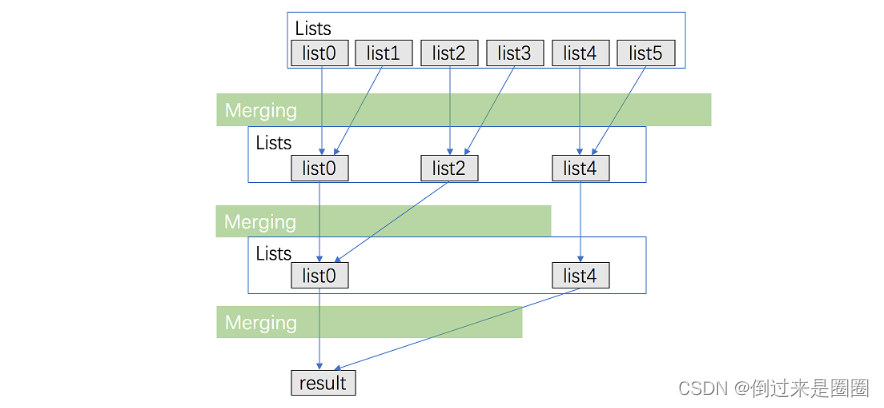
分治合并

类似归并排序，将相邻链表两两合并，直到合成最终的升序链表

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if(lists.length==0) return null;
        return merge(lists,0,lists.length-1);
    }
    public ListNode merge(ListNode[] lists,int l,int r){
        if(l==r)
            return lists[l];
        int mid=(l+r)/2;
        ListNode n1=merge(lists,l,mid);
        ListNode n2=merge(lists,mid+1,r);
        return merge2Lists(n1,n2);
    }
    //合并两个有序链表
    public ListNode merge2Lists(ListNode a,ListNode b){
        if(a==null||b==null)
            return b==null?a:b;
        ListNode head=new ListNode();
        ListNode p=a,q=b,tail=head;
        while(p!=null&&q!=null){
            if(p.val<q.val){
                tail.next=p;
                p=p.next;
            }
            else{
                tail.next=q;
                q=q.next;
            }
            tail=tail.next;
        }
        tail.next=p!=null?p:q;//剩余的非空链
        return head.next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

时间复杂度：$O(kn\ast logk)$，每轮合并$k/2^i$组链表，每一组合并的时间代价是$2^{i}n$，故每轮时间复杂度为$kn$，共$logk$轮。

空间复杂度：$O(logk)$，递归栈所需要的空间。

优先队列合并

K个链表，每个链表赋一个指针，每次从K个指针指向的元素中选一个最小的，链接到新链表尾部，挑选最小指针的过程可以用最小堆优化，即优先队列。

class Solution {
    //定义优先队列内元素,按照结点的值升序排序
    class Status implements Comparable<Status>{
        private int val;
        private ListNode node;
        public Status(int value,ListNode p){
            this.val=value;
            this.node=p;
        }
        public int compareTo(Status s){
            return this.val-s.val;
        }
    }
    //定义优先队列
    Queue<Status>queue=new PriorityQueue<>();

    public ListNode mergeKLists(ListNode[] lists) {
        ListNode head=new ListNode();
        ListNode tail=head;
        //所有非空链表头结点入队
        for(ListNode node:lists){
            if(node!=null)
                queue.offer(new Status(node.val,node));
        }
        //合并K个升序链表
        while(!queue.isEmpty()){
            //最小的结点链接到新链表尾部
            Status tmp=queue.poll();
            ListNode node=tmp.node;
            tail.next=node;
            tail=tail.next;
            //node所在链表指针向后移动一位
            if(node.next!=null){
                queue.offer(new Status(node.next.val,node.next));
            }
        }
        return head.next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

时间复杂度：$O(kn\ast logk)$，最多$kn$个结点，每次插入删除时间复杂度为logk，所以时间复杂度为$O(kn\ast logk)$。

空间复杂度：$O(k)$，优先队列所需要的空间，其中元素不超过k个。