-
基于竞争学习的粒子群优化算法-附代码
基于竞争学习的粒子群优化算法
摘要:针对传统PSO算法容易陷入局部最优的问题,提出一种基于竞争学习的粒子群优化算法(CLPSO);在CLPSO中,首先通过动态计算粒子的适应度值将种群分成优选、合理和疏离3个子群;其次,根据3个子群中粒子的进化特性,为3个子群分别设计了不同的更新变异方式;然后,利用12个基准测试函数对算法的性能进行了验证;实验结果表明,所提的竞争学习策略能够有效克服经典PSO算法在处理复杂多峰问题时容易陷入局部最优的缺陷;1.粒子群优化算法
基础粒子群算法的具体原理参考网络资料
2. 改进粒子群算法
2.1 竞争学习机制
本文提出新颖的竞争学习机制来指导粒子调 整飞行状态, 起到提高 PSO 处理复杂多峰优化问题 能力的目的。竞争学习机制的核心是将种群分类。 传统的 PSO 算法中粒子的更新方式单一, 所有的粒 子不论好坏共用同一种更新方式, 因此种群缺乏多 样性易陷入局部最优。本文所提算法则针对已分组 的 3 组粒子的各自特点, 设计三种独特的更新策略, 使每个粒子都能及时调整飞行状态, 向全局最优靠 近, 最终 3 个子群的输出形成新种群 P ( t + 1 ) \mathrm{P}(t+1) P(t+1) 。
在 CLPSO 中, 通过自适应分区操作, 每个粒 子都参与了适应度值竞争, 增强了种群的多样性, 扩大了粒子的搜索范围, 能够有效避免种群陷入局 部最优。下面具体介绍子群的划分依据和每个子群 的更新策略。
首先, 求出所有粒子的适应度值, 按照从小到 大排序, 再根据适应度值的平均值和标准差对种群 中粒子进行分组。平均值和标准差的具体计算公式 如下:
f ˉ = ∑ i = 1 M f i M (3)\tag{3} fˉ=M∑i=1Mfi(3)f ¯ = ∑ i = 1 M f i M σ = 1 M ∑ i = 1 M ( f i − f ˉ ) (4) \sigma=\sqrt{\frac{1}{M} \sum_{i=1}^{M}\left(f_{i}-\bar{f}\right)} \tag{4} σ=M1i=1∑M(fi−fˉ)(4)
其中, f i f_{i} fi 为第 i i i 个粒子的适应度值, N N N 为粒子个数,
f ˉ \bar{f} fˉ 为粒子适应度值的平均值, σ \sigma σ 为粒子适应度值的 标准差。
在划分子群时, 首先标记出最靠近平均适应度 值的粒子, 再以标准差为半径设定合理区粒子的范 围, 进一步得出疏离区粒子和优选区粒子。针对不同的子群, 本文分别设计了不同的更新 机制。优选区粒子距离种群最优位置较近, 为了避 免陷入局部最优, 需要增强全局探索能力, 因此利 用改进的柯西公式设计了自我变异的更新机制。 变异后的柯西公式即为优选区粒子更新公式如下:
x i j p ( t + 1 ) = x i j p ( t ) ⋅ ( 1 + n t ⋅ C ( 0 , 1 ) ) (5) x_{i j}^{p}(t+1)=x_{i j}^{p}(t) \cdot\left(1+n_{t} \cdot C(0,1)\right) \tag{5} xijp(t+1)=xijp(t)⋅(1+nt⋅C(0,1))(5)n t = t m a x − t t max (6) n_{t}=\frac{t_{\mathrm{max}}-t}{t_{\max }} \tag{6} nt=tmaxtmax−t(6)
其中: n t n_{t} nt 为控制变异步长的参数, C ( 0 , 1 ) C(0,1) C(0,1) 是由柯西分 布函数产生的随机数。 x i j p x_{i j}^{p} xijp 表示优选区粒子的位置。 t max t_{\text {max }} tmax 为最大迭代次数, t t t 为当前迭代次数。从公式(6) 可以看出, n t n_{t} nt 能够随着迭代次数的增加而自适应减 小, 起到了平衡优选区粒子的探索和开发的作用。 在进化前期, 需要设置一个较大的变异因子值, 使 得粒子能够跳出局部最优; 反之, 在进化后期, 需 要设置一个较小的变异因子值, 以加快算法的收敛 速度。因此, 本文采用了公式(6)所示的自适应策略。 疏离区粒子距离种群最优位置较远, 为了加快 向可能的全局最优解逼近的速度, 该区域粒子主要 是向优选区粒子进行学习。
疏离区粒子更新公式为:
x i j A ( t + 1 ) = c 1 x A i j ( t ) + c 2 ( x i j i j ( t ) − x p k j ( t ) ) + c 3 α ( f ˉ − x i j ( t ) ) (7)\tag{7} xijA(t+1)=c1xAij(t)+c2(xijij(t)−xpkj(t))+c3α(fˉ−xij(t))(7)x i j A ( t + 1 ) = c 1 x A i j ( t ) + c 2 ( x i j i j ( t ) − x p k j ( t ) ) + c 3 α ( f ¯ − x i j ( t ) )
其中, c 1 、 c 2 c_{1} 、 c_{2} c1、c2 和 c 3 c_{3} c3 为加速因子。从公式(7)可以看出, x i j A ( t + 1 ) x_{i j}^{A}(t+1) xijA(t+1) 是由三部分组成, 第一部分和标准 PSO 更 新公式的第一部分相同; 第二部分中 x P k j ( t ) x^{P}{ }_{k j}(t) xPkj(t) 为优选 区的粒子, 这部分表示疏离区粒子以优选区粒子为 学习对象进行状态更新; 第三部分引入新的参数 α \alpha α ( α \alpha α 为一个较小的正数), 这部分表示粒子更新过程 还受粒子中心位置的牵制, 作用是控制粒子的更新 范围, 增强算法的收敛性。
合理区粒子需要自适应平衡全局搜索和局部 开发, 因此为合理区粒子设计了竞争切换机制。合 理区粒子更新公式分两种情况:1)当种群末陷入局 部最优时, 合理区粒子采用传统的粒子更新方式(公 式 1 、 2 ) 1 、 2) 1、2) 来更新状态, 目的是保证种群向全局最优 解逐步逼近, 保证算法收玫性; 2)当种群陷入局部 最优时, 粒子当前位置的适应度值与上一次迭代产 生的适应度值相同, 即 f ( x i ) t − f ( x i ) t − 1 = 0 f\left(x_{i}\right)^{t}-f\left(x_{i}\right)^{t-1}=0 f(xi)t−f(xi)t−1=0 时, 合理区粒 子采用公式(5)来更新状态, 目的是通过自身变异增 强种群搜索能力, 增加跳出局部最优的机率。3.实验结果
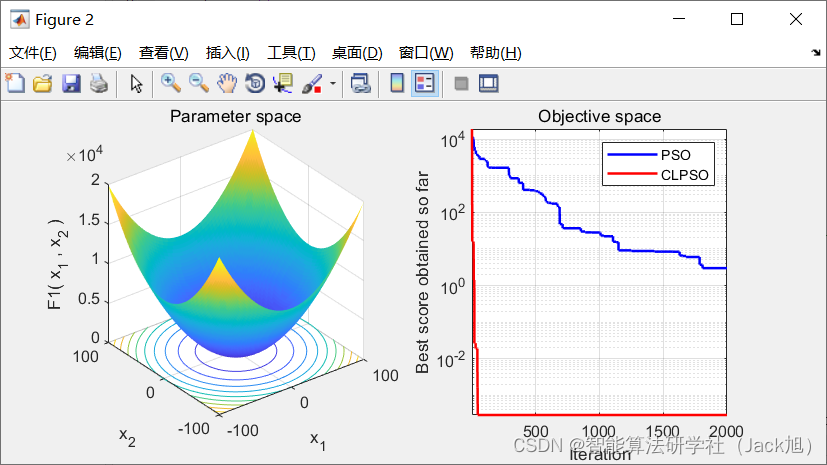
4.参考文献
[1]张钰,王蕾,周红标,赵环宇.基于竞争学习的粒子群优化算法设计及应用[J/OL].计算机测量与控制:1-9[2021-06-18].http://kns.cnki.net/kcms/detail/11.4762.TP.20210527.0930.008.html.
5.Matlab代码
6.Python代码
-
相关阅读:
Vue.use()和install的小知识
java毕业设计智能推荐的医药知识推广平台统Mybatis+系统+数据库+调试部署
温振一体化变送器优势
zlMediaKit 4 buffer模块--buffer什么都能装&不只有send还有sendmsg/sendmmsg
MySQL中from_unixtime和unix_timestamp处理数据库时间戳转换问题-案例
基于模糊测试方法实现车载通信测试
OpenCV图像处理——(实战)答题卡识别试卷
node 格式化时间的传统做法与高级做法(moment)
电气工程及其自动化
Vue开发中Jwt的使用
- 原文地址:https://blog.csdn.net/u011835903/article/details/126697525