三分类网络的物理意义是什么?

(A，B)---m*n*k---(1,0)(0,1)

对于一个二分类网络可以将被分类的A和B分别理解为粒子和环境，因为粒子处于环境中。于是A和B之间的距离可以理解为0。因为t=s/v，则即便A和B之间的相互作用的速度小于光速，A和B之间仍然可以实现瞬时作用，并不违反理论。

( A, B, C )---m*n*k---( 1, 0, 0 )( 0, 1, 0 )( 0, 0, 1 )

对于一个三分类网络要完成3次形态的变换。A⇋B，A⇋C，B⇋C，每一次形态变换就是一次二分类，因此对于一个三分类网络可以理解为由3个二分类网络组成

(A，B)---m*n*k---(1,0)(0,1)

(A，C)---m*n*k---(1,0)(0,1)

(B，C)---m*n*k---(1,0)(0,1)

 这就意味着存在3对瞬时作用，也就表明这3个粒子彼此之间的距离都是0.随着时间的推移网络的收敛误差会不断减小，而网络的分类准确率会不断变大。这个过程意味着A被错误的分成B和C的成分少了，同样B被错误的分成A和C，C被错误的分成A和B的成分也少了。

所以这个三分网络可以被解释为，3个距离为0的粒子不断的相互作用，随着时间的演化，最终变得越来越像自己。

而前面的实验表明相同收敛误差下，迭代次数取决于等位点差的绝对值的和，这次就继续验证这一猜测。

用的训练集是mnist的0，1，2，3，4，的第一张图片。用间隔取点的办法化成13*13.

( 0, 1, 2 )---169*30*3---( 1, 0, 0 )( 0, 1, 0 )( 0, 0, 1 )这个网络简记为0*1*2.就只有3张图片不断循环往复，直到收敛。共进行了10组得到数据

将收敛误差为7e-4的迭代次数画成图

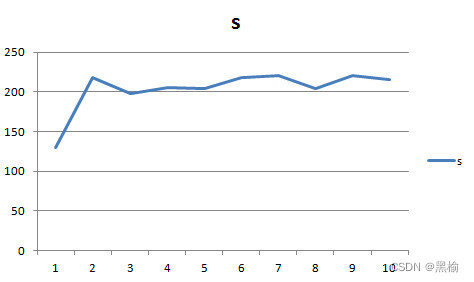
再将移位距离S的曲线画成图

在这组数据中s和n之间的反比关系依然存在。

移位距离假设

(A，B)---m*n*k---(1,0)(0,1)

用神经网络分类A和B，把参与分类的A和B中的数字看作是组成A和B的粒子，分类的过程就是让A和B中的粒子互相交换位置，寻找最短移位路径的过程。而熵H与最短移位距离S成正比，迭代次数n与S成反比。

移位规则汇总

移位距离就是等位点数值差的绝对值的和S=Σ|a-b|，如果训练集有多张图片取平均值，如果是多分类问题则移位距离为所有两两组合移位距离的和。

如对一组3*3的矩阵

S=s0+s1+，…，+s8=|a0-b0|+|a1-b1|+,…,+|a8-b8|

如果是3分类问题，就应该实现3个形态之间的两两分类，也就是要完成3对等位点之间的差。

因此移位距离

S=Sab+Sac+Sbc=

|a0-b0|+|a1-b1|+|a2-b2|+|a3-b3|+

|a0-c0|+|a1-c1|+|a2-c2|+|a3-c3|+

|b0-c0|+|b1-c1|+|b2-c2|+|b3-c3|