-
禁忌搜索算法TS求解连续函数最值
目录
一、局部邻域搜索
局部邻域搜索是基于贪婪准则持续地在当前的邻域中进行搜索,虽然算法通用,易于实现,且容易理解,但其搜索性能完全依赖于邻域结构和初始解,尤其容易陷入局部极小值无法保证全局优化
算法可以描述为:
1)选定一个初始可行解:
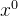 ;记录当前最优解
;记录当前最优解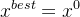 ,
,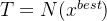 ,其中
,其中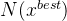 表示
表示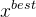 的邻域。
的邻域。2)当
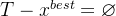 (空集),或满足其他停止运算准则是,输出计算结果,停止运算,否则,继续步骤3)
(空集),或满足其他停止运算准则是,输出计算结果,停止运算,否则,继续步骤3)3)从中选一个集合
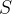 ,得到
,得到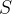 中的最好解
中的最好解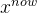 。若
。若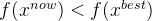 ,则
,则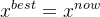 ,
,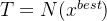 ;否则,
;否则,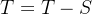 ,重复步骤2),继续搜索
,重复步骤2),继续搜索这种邻域搜索的方法易于理解,易于实现,而且具有很好的通用性,但是搜索结果的好坏完全依赖于初始解和邻域的结构。
二、禁忌搜索
对于一个初始解,在一种邻域范围内对其进行一系列变化,从而得到许多候选解。从这些候选解中选出最优候选解,将候选解对应的目标值于best-so-far状态进行比较。若其目标值优于best-so-far状态,就将该候选解解禁,用来替代当前最优解及其best-so-far状态,然后将其加入禁忌表,再将禁忌表中相应对象的禁忌长度改变;如果候选解的目标值都不优于best-so-far,就从候选解中选出不属于禁忌对象的最佳状态,并将其作为新的当前解,不用与当前解比较,直接将其所对应的对象作为禁忌对象,并将禁忌表中相应对象的禁忌长度进行修改。
三、禁忌搜索算法流程
禁忌搜索算法基本思想是:给定一个当前解(初始解)和一种邻域,然后在当前解的邻域中确定若干候选解;若候选解对应的目标值优于best-so-far状态,并将相应的对象加入禁忌表,同时修改禁忌表中各对象的任期,若不存在上述候选解,则在候选解中选择非禁忌的最佳状态为新的当前解,而无视它与当前解的优劣,同时将相应的对象加入禁忌表,并修改禁忌表中各对象人气。如此重复,直到满足停止准则。算法步骤可描述如下:
1)给定禁忌搜索算法参数,随机产生初始解
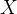 ,置禁忌表为空。
,置禁忌表为空。2)判断算法终止条件是否满足:若是,则结束算法并输出优化结果;否则继续以下步骤
3)利用当前解的邻域函数产生其所有邻域解,并从中确定若干候选解
4)对候选解判断藐视准则是否满足:若满足,则利用满足藐视准则的最佳状态替代x成为当前解,即x=y,并用对应的禁忌对象替换最早进入禁忌表的禁忌对象,同时用y替换best-so-far状态,然后转到步骤6);否则继续以下步骤
5)判断候选解对应的各对象的禁忌属性,选择候选解集中非禁忌对象的对应的最佳状态为新的当前解,同时用与之对应的禁忌对象替换最早进入禁忌表的禁忌对象
6)判断算法终止条件是否满足

四、算法求解例题
求函数
 的最大值,其中
的最大值,其中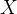 的取值范围为
的取值范围为![[-5,5]](https://1000bd.com/contentImg/2023/10/29/181851381.png) ,
,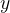 的取值范围为
的取值范围为![[-5,5]](https://1000bd.com/contentImg/2023/10/29/181851381.png) 。这是一个有多个局部极值问题,其函数图像如下。
。这是一个有多个局部极值问题,其函数图像如下。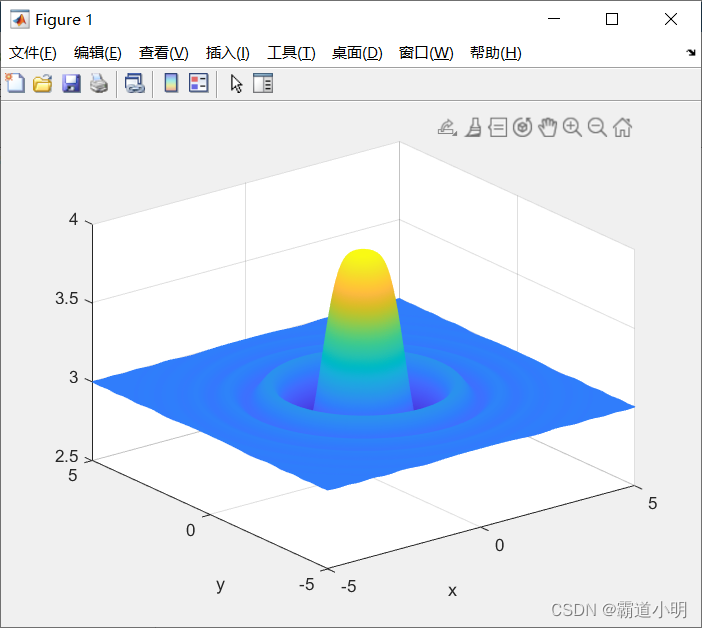
解:仿真过程如下:
(1)初始化禁忌长度TabuL为5~11之间的随机整数,邻域解个数Ca=5。最大迭代次数G= 200,禁忌表为Tabu.
(2)随机产生一 初始解,计算其适配值,记为目前最优解bestsofar和当前解xnow;产生5个邻域解,计算其适配值,将其中最优解作为候选解candidate.
(3)计算候选解candidate与当前解xnow的差值deltal, 以及它与目前最优解bestsofar的差值delta2。 当delta1<0时,把候选解candidate赋给下一次迭代的当前解xnow,并更新禁忌表Tabu.
(4)当delta1>0, 同时delta2>0时,把候选解candidate赋给下一次迭代的当前解xnow和目前最优解bestsofar,并更新禁忌表Tabu.
(5) 当delta1>0, 同时delta2<0时,判断候选解candidate是否在禁忌表中:若不在,则把候选解candidate 赋给下一次迭代的当前解xnow,并更新禁忌表Tabu;若在,则用当前解xnow重新产生邻域解。
(6)判断是否满足终止条件:若满足,则结束搜索过程,输出优化值;若不满足,则继续进行迭代优化。
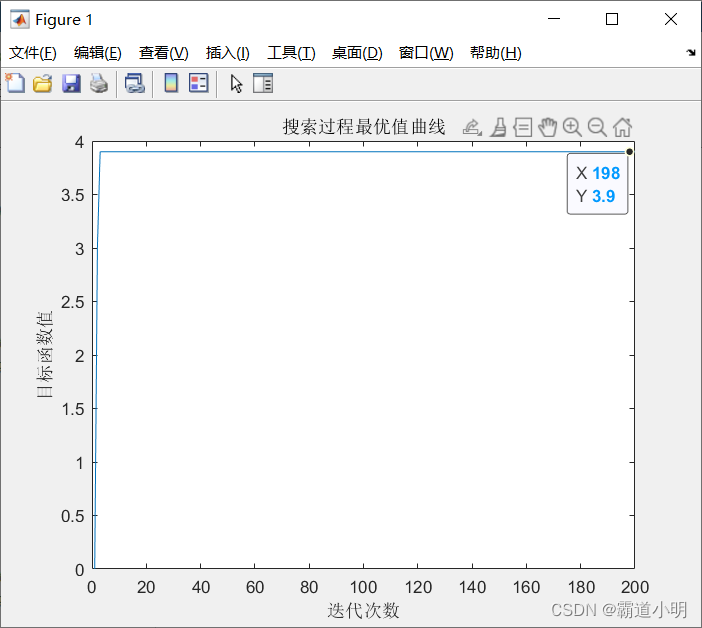
优化搜索结束后,其最优值曲线如图8.5所示,优化后的结果为x = 0.045,
y= -0.0366,函数f(x, y)的最大值为3.9。
- %%%%%%%%%%%%%%%%禁忌搜索算法求函数极值问题%%%%%%%%%%%%%%%%%%%
- %%%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%
- clear all; %清除所有变量
- close all; %清图
- clc; %清屏
- xu=5; %上界
- xl=-5; %下界
- L=randi([5,11],1,1); %禁忌长度取5,11之间的随机数
- Ca=5; %邻域解个数
- Gmax=200; %禁忌算法的最大迭代次数;
- w=1; %自适应权重系数
- tabu=[]; %禁忌表
- x0=rand(1,2)*(xu-xl)+xl; %随机产生初始解
- bestsofar.key=x0; %最优解
- xnow(1).key=x0; %当前解
- %%%%%%%%%%%%%%%%最优解函数值,当前解函数值%%%%%%%%%%%%%%%%%
- bestsofar.value=func2(bestsofar.key);
- xnow(1).value=func2(xnow(1).key);
- g=1;
- while g
- x_near=[]; %邻域解
- w=w*0.998;
- for i=1:Ca
- %%%%%%%%%%%%%%%%%%%%%产生邻域解%%%%%%%%%%%%%%%%%%%%
- x_temp=xnow(g).key;
- x1=x_temp(1);
- x2=x_temp(2);
- x_near(i,1)=x1+(2*rand-1)*w*(xu-xl);
- %%%%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%%%%%
- %%%%%%%%%%%%%%%%%%%边界吸收%%%%%%%%%%%%%%%%%%%%%
- if x_near(i,1)x_near(i,1)=xl;endif x_near(i,1)>xux_near(i,1)=xu;endx_near(i,2)=x2+(2*rand-1)*w*(xu-xl);%%%%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%边界吸收%%%%%%%%%%%%%%%%%%%%%if x_near(i,2)x_near(i,2)=xl;endif x_near(i,2)>xux_near(i,2)=xu;end%%%%%%%%%%%%%%计算邻域解点的函数值%%%%%%%%%%%%%%%%%%%fitvalue_near(i)=func2(x_near(i,:));end%%%%%%%%%%%%%%%%%%%%最优邻域解为候选解%%%%%%%%%%%%%%%%%%%temp=find(fitvalue_near==max(fitvalue_near));candidate(g).key=x_near(temp,:);candidate(g).value=func2(candidate(g).key);%%%%%%%%%%%%%%候选解和当前解的评价函数差%%%%%%%%%%%%%%%%%%delta1=candidate(g).value-xnow(g).value;%%%%%%%%%%%%%%候选解和目前最优解的评价函数差%%%%%%%%%%%%%%%delta2=candidate(g).value-bestsofar.value;%%%%%候选解并没有改进解,把候选解赋给下一次迭代的当前解%%%%%%if delta1<=0xnow(g+1).key=candidate(g).key;xnow(g+1).value=func2(xnow(g).key);%%%%%%%%%%%%%%%%%%%%%更新禁忌表%%%%%%%%%%%%%%%%%%%%%%%tabu=[tabu;xnow(g+1).key];if size(tabu,1)>Ltabu(1,:)=[];endg=g+1; %更新禁忌表后,迭代次数自增1%%%%%%%如果相对于当前解有改进,则应与目前最优解比较%%%%%%%%%%elseif delta2>0 %候选解比目前最优解优%%%%%%%%%%把改进解赋给下一次迭代的当前解%%%%%%%%%%%%xnow(g+1).key=candidate(g).key;xnow(g+1).value=func2(xnow(g+1).key);%%%%%%%%%%%%%%%%%%%%更新禁忌表%%%%%%%%%%%%%%%%%%%%%tabu=[tabu;xnow(g+1).key];if size(tabu,1)>Ltabu(1,:)=[];end%%%%%%%%把改进解赋给下一次迭代的目前最优解%%%%%%%%%%%%%%%%%%%%%%%%%%%%%包含藐视准则%%%%%%%%%%%%%%%%%%%%%%%bestsofar.key=candidate(g).key;bestsofar.value=func2(bestsofar.key);g=g+1; %更新禁忌表后,迭代次数自增1else%%%%%%%%%%%%%%%判断改进解时候在禁忌表里%%%%%%%%%%%%%%%[M,N]=size(tabu);r=0;for m=1:Mif candidate(g).key(1)==tabu(m,1)...& candidate(g).key(2) == tabu(m,1)r=1;endendif r==0%%改进解不在禁忌表里,把改进解赋给下一次迭代的当前解xnow(g+1).key=candidate(g).key;xnow(g+1).value=func2(xnow(g+1).key);%%%%%%%%%%%%%%%%%%%%%更新禁忌表%%%%%%%%%%%%%%%%%%tabu=[tabu;xnow(g).key];if size(tabu,1)>Ltabu(1,:)=[];endg=g+1; %更新禁忌表后,迭代次数自增1else%%%如果改进解在禁忌表里,用当前解重新产生邻域解%%%%%xnow(g).key=xnow(g).key;xnow(g).value=func2(xnow(g).key);endendendtrace(g)=func2(bestsofar.key);endbestsofar; %最优变量及最优值figureplot(trace);xlabel('迭代次数')ylabel('目标函数值')title('搜索过程最优值曲线')%%%%%%%%%%%%%%%%%%%%%%%%%%%%适配值函数%%%%%%%%%%%%%%%%%%%%%%%%function y=func2(x)y=(cos(x(1)^2+x(2)^2)-0.1)/(1+0.3*(x(1)^2+x(2)^2)^2)+3;end
-
相关阅读:
位图的基本原理以及应用
javaScript贪吃蛇
R 语言 |普通矩阵怎么保存为稀疏矩阵的3列(i, j, x)格式?
KY33 密码翻译
linux scsi命令读取文件
text/xml和application/xml
CSS之复合选择器与伪类选择器
09 -- 回文对
涉及主页面内嵌iframe中的列表数据的保存
神经网络结构设计,神经网络架构设计
- 原文地址:https://blog.csdn.net/qq_54169998/article/details/126689928
