数学建模学习笔记（7）：相关系数

相关系数概述

相关系数用来衡量两个变量之间线性相关性的大小。根据数据满足的不同条件，需要选择不同的相关系数进行计算和分析。常用的两种相关系数分别是皮尔逊相关系数和斯皮尔曼相关系数。

皮尔逊相关系数的相关概念

①皮尔逊相关系数可以视为消除了量纲影响后的协方差。

②皮尔逊相关系数的本质是一种线性相关系数，因此只有事先通过散点图确定两个变量是线性相关的，皮尔逊相关系数才是有意义的。

③非线性相关的两组数据线性相关系数也可能很大，因为离群点和异常点对相关系数的影响很大。

④皮尔逊相关系数小不代表两个变量之间不存在相关性，因为还可能存在非线性的其他相关关系。

在进行数据处理时，最好首先对数据进行一个简单的描述性统计，使用的软件可以是Excel或者SPSS。同时也可以使用SPSS作出矩阵散点图来观察两个变量之间是否存在较为明显的线性相关性。

SPSS进行数据描述性统计步骤：导入数据Excel表格→分析→描述统计→描述
SPSS进行散点图绘制步骤：导入数据Excel表格→图形→旧对话框→散点图

对相关系数的解释需要依赖于具体的应用背景和目的。相对于相关系数的大小，我们往往更加关注相关系数的显著性，因此常常需要对相关系数是否显著异于零进行假设检验。

假设检验的一般步骤

①确定原假设和备择假设。其中原假设和备择假设相互对立；

②根据需要检验的统计量构造一个分布。一般该分布可以通过查阅资料的方式获取；

③作出该分布的概率密度函数pdf图。

④根据自身的实际需求给出一个置信水平（一般取90%、95%或99%）。置信水平的互补数称为显著性水平。

⑤计算和判定：代入数值计算出统计量所在的区间是接受域或拒绝域，从而确定是否接受原假设。

假设检验还可以采用P值检验法：首先求出代入数值计算出的统计量所对应的概率，再用1减去该概率得到P值，最后与显著性水平进行比较。注意双侧检验的P值要同时考虑两边的。

皮尔逊相关系数的假设检验方法

①确定原假设和备择假设：原假设是相关系数为零，备择假设是相关系数不为零。

②构造如下图所示的统计量：

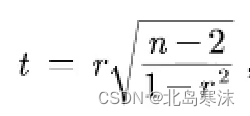
可以证明t服从自由度为n-2的t分布。

③将检验值代入统计量中，得到一个特定的检验值。

④通过查表的方式获取临界值，通过P值检验法判断原假设是否成立（也可以通过一般方法）。

备注：可以通过SPSS软件在计算相关系数的同时进行显著性标记。显著性标记越多，则相关系数越异于零。

皮尔逊相关系数假设检验条件

①实验数据通常假设来自于正态分布的总体；

②实验数据之间的差距不能太大，也就是存在异常值；

③每组样本之间采用独立抽样。

这三个条件中，后面两个条件一般可以默认成立，但是第一个条件相当重要，因此进行皮尔逊相关系数的假设检验前，需要对样本数据进行正态分布检验。

正态分布常用的三种检验方法

①JB检验（雅克-贝拉检验）：根据偏度和丰度进行检验，适用于样本数大于30的情况。可以使用Matlab进行JB检验。

②夏皮洛-威尔克检验：适用于样本量在3-50之间的正态分布检验，可以使用SPSS实现。

③Q-Q图：Q-Q图是一种适用于样本量很大情况下的正态分布检验方法，可以通过Matlab实现。如果Q-Q图上的点近似在一条直线附近则说明数据服从正态分布。可以使用Matlab进行Q-Q图检验。

斯皮尔曼相关系数

当两组数据不满足正态分布，以至于不能使用假设检验时，则需要使用对数据要求更低的斯皮尔曼相关系数，也称为等级相关系数。斯皮尔曼相关系数的计算如下所示：

①首先计算出各列数据的等级（将一列数字按照从小到大排序后这个数所在的位置），如果有数值相同，则取算术平均值。

②代入如下公式即可求出斯皮尔曼相关系数：

可以使用Matlab计算斯皮尔曼相关系数。

斯皮尔曼相关系数的检验：

• 如果样本数小于等于30（小样本情况），则可以通过查斯皮尔曼等级临界值表进行检验。只有计算出的相关系数大于等于临界值，才能得出相关系数显著的结论。
• 对于样本数较多的情况，构造如下图所示的统计量：
  -
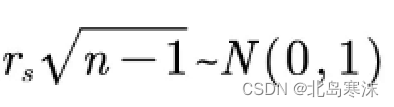
  代入计算出P值，与显著性水平进行比较即可得出结论：如果大于显著性水平则说明相关系数与零无显著差异。

相关系数的选择方式

①对于连续的、满足正态分布和线性关系的数据，优先考虑使用皮尔逊相关系数（斯皮尔曼相关系数也可以使用，但是皮尔逊相关系数效率更高）。

②上述任意一个条件不满足，只能使用斯皮尔曼相关系数。

③定序数据之间只能使用斯皮尔曼相关系数（定序数据是仅仅反映对象等级和顺序关系的表示类别的数据）。

使用相关系数的一般步骤

1. 散点图线性相关分析：对两个变量使用SPSS作出散点图，定性判断两个变量之间是否存在线性相关关系。如果存在线性相关关系，则进行后续步骤，否则过程结束。
2. 检验两组变量是否都满足正态分布：根据样本量的大小，使用雅克贝拉检验、夏皮洛威尔克检验或QQ图检验。如果满足则进入下一步，不满足则进入第4步。
3. 求出皮尔逊相关系数并进行假设检验：使用SPSS求解并检验皮尔逊相关系数的显著性，判断相关系数是否显著异于零。
4. 求出斯皮尔曼相关系数并进行假设检验：使用SPSS求解并检验斯皮尔曼相关系数的显著性，判断相关系数是否显著异于零。
5. 分析并下结论：如果得到的皮尔逊相关系数或斯皮尔曼相关系数显著异于零，则进行分析并下结论。

备注：在使用散点图进行线性相关分析之前最好也对变量进行一个描述性统计分析。