遗传算法GA求解TSP问题

目录

一、遗传算法基本思想

二、遗传算法的主要步骤

三 、遗传编码

1.二进制编码

2.实数编码

四、遗传算法流程

五、例题

---

一、遗传算法基本思想

遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。

二、遗传算法的主要步骤

（1）编码：将问题的候选解用染色体表示，实现解空间向编码空间的映射过程。遗传算法不直接处理解空间的决策变量，而是将其转换成由基因按一定结构组成的染色体。编码方式有很多，如二进制编码、实数向量编码、整数排列编码、通用数据结构编码等等。本文将采用二进制编码的方式，将十进制的变量转换成二进制，用0和1组成的数字串模拟染色体，可以很方便地实现基因交叉、变异等操作。 

（2）种群初始化：产生代表问题可能潜在解集的一个初始群体（编码集合）。种群规模设定主要有以下方面的考虑：从群体多样性方面考虑，群体越大越好，避免陷入局部最优；从计算效率方面考虑，群体规模越大将导致计算量的增加。应该根据实际问题确定种群的规模。产生初始化种群的方法通常有两种：一是完全随机的方法产生；二是根据先验知识设定一组必须满足的条件，然后根据这些条件生成初始样本。

（3）计算个体适应度：利用适应度函数计算各个个体的适应度大小。适应度函数（Fitness Function）的选取直接影响到遗传算法的收敛速度以及能否找到最优解，因为在进化搜索中基本不利用外部信息，仅以适应度函数为依据，利用种群每个个体的适应程度来指导搜索。

（4）进化计算：通过选择、交叉、变异，产生出代表新的解集的群体。选择（selection）：根据个体适应度大小，按照优胜劣汰的原则，淘汰不合理的个体；交叉（crossover）：编码的交叉重组，类似于染色体的交叉重组；变异（mutation）：编码按小概率扰动产生的变化，类似于基因突变。

（5）解码：末代种群中的最优个体经过解码实现从编码空间向解空间的映射，可以作为问题的近似最优解。这是整个遗传算法的最后一步，经过若干次的进化过程，种群中适应度最高的个体代表问题的最优解，但这个最优解还是一个由0和1组成的数字串，要将它转换成十进制才能供我们理解和使用。

三 、遗传编码

遗传编码将变量转化为基因组的表示形式，优化变量的编码机制有二进制编码、十进制编码（实数编码）等。

1.二进制编码

这里简单介绍以下二进制编码的实现原理。例如，求实数区间上函数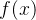的最大值，传统的方法是不断调整自变量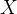的值，假设使用二进制编码新式，我们可以由长度6的未穿表示变量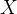，即从000000到111111，并将中间的取值映射到实数区间内。由于哦才能够整数上来看，6位长度二进制表示范围为0~63，所以对应的区间，每个相邻值之间的阶跃值为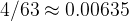。这个就是编码的精度，编码精度越高，所得到的解的质量也越高。

2.实数编码

在解决高维、连续优化问题等是，经常采用实数编码方式。实数编码的优点是计算精度搞，便于和经典连续优化算法结合。

四、遗传算法流程

1）初始化。设置进化代数计数器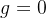，设置最大进化代数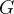，随机生成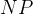个个体作为初始群体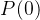

2）个体评价。计算群体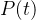中各个个体的适应度

3）选择运算。将选择算子作用域群体，根据个体适应度，按照一定的规则和方法，选择一些优良个体遗传到下一代群体。

4）交叉运算。将交叉算子作用于群体，对选中的成对个体，以某一概率交换他们之间的部分染色体，产生新的个体

5）变异运算。将变异算子作用于群体，对选中的个体，以某一概率改变某一个或某一些基因值为其他的等位基因。群体P(t)经过选择、交叉、和变异运算之后得到下一代群体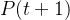。计算其适应度值，并根据适应度值进行排序，准备进行下一代遗传操作。

6）终止条件判断：若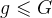，则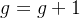，转到步骤2）；若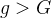，则终止计算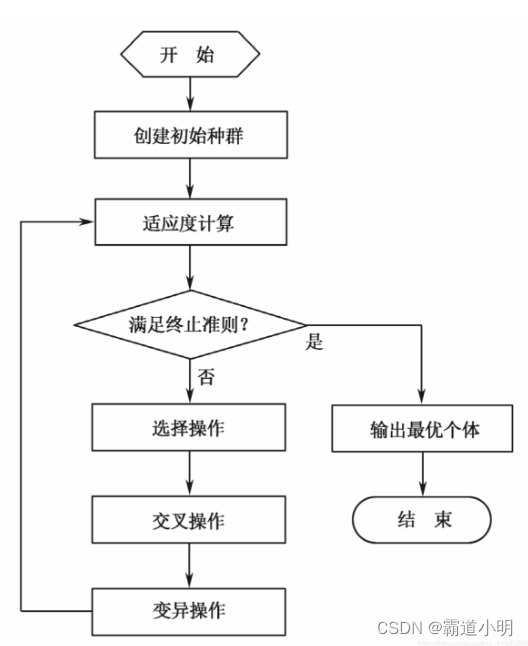

五、例题

    旅行商问题（TSP问题）。假设有一个旅行商人要拜访全国31个省会城市，他需要选择所要走的路径，路径的限制是每个城市只能拜访一次，二球要最后回到原来出发的城市。路径的选择要求是：所选的路径的路程之和中的最小。

    全国31个省会的坐标为[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;3238 1229;4196 1044;4312  790;4386  570;3007 1970;2562 1756;2788 1491;2381 1676;1332  695;3715 1678;3918 2179;4061 2370;3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;2370 2975]

仿真过程如下：

1）初始化种群数目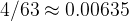，染色体基因维数，最大进化代数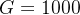

2）产生初始化种群，计算个体适应度值，并进行归一化；采用基于概率的方式选择进行操作的个体，对选中的成对个体，随机交叉所选中的成对城市坐标，以确保交叉后路径每个城市只到访一次；对选中的单个个体，随机交换其中一对城市坐标作为变异操作，产生新的种群，进行下一次遗传操作。

3）判断是否满足条件：若满足，则结束搜索

%%%%%%%%%%%%%%%%%%%%%%%%%遗传算法解决TSP问题%%%%%%%%%%%%%%%%%%%%%%%
clear all;                      %清除所有变量
close all;                      %清图
clc;                            %清屏
C=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
    3238 1229;4196 1044;4312  790;4386  570;3007 1970;2562 1756;...
    2788 1491;2381 1676;1332  695;3715 1678;3918 2179;4061 2370;...
    3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
    3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
    2370 2975];                 %31个省会城市坐标
N=size(C,1);                    %TSP问题的规模,即城市数目
D=zeros(N);                     %任意两个城市距离间隔矩阵
%%%%%%%%%%%%%%%%%%%%%求任意两个城市距离间隔矩阵%%%%%%%%%%%%%%%%%%%%%
for i=1:N
    for j=1:N
        D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
    end
end
NP=200;                          %种群规模
G=1000;                          %最大遗传代数
f=zeros(NP,N);                   %用于存储种群
F=[];                            %种群更新中间存储
for i=1:NP
    f(i,:)=randperm(N);          %随机生成初始种群
end
R=f(1,:);                        %存储最优种群
len=zeros(NP,1);                 %存储路径长度
fitness=zeros(NP,1);             %存储归一化适应值
gen=0;
%%%%%%%%%%%%%%%%%%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
while gen<G
    %%%%%%%%%%%%%%%%%%%%%计算路径长度%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    for i=1:NP
        len(i,1)=D(f(i,N),f(i,1));
        for j=1:(N-1)
            len(i,1)=len(i,1)+D(f(i,j),f(i,j+1));
        end
    end
    maxlen=max(len);              %最长路径
    minlen=min(len);              %最短路径
    %%%%%%%%%%%%%%%%%%%%%%%%%更新最短路径%%%%%%%%%%%%%%%%%%%%%%%%%%
    rr=find(len==minlen);
    R=f(rr(1,1),:);
    %%%%%%%%%%%%%%%%%%%%%计算归一化适应值%%%%%%%%%%%%%%%%%%%%%%%%%%
    for i=1:length(len)
        fitness(i,1)=(1-((len(i,1)-minlen)/(maxlen-minlen+0.001)));
    end
    %%%%%%%%%%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    nn=0;
    for i=1:NP
        if fitness(i,1)>=rand
            nn=nn+1;
            F(nn,:)=f(i,:);
        end
    end
    [aa,bb]=size(F);
    while aa<NP
        nnper=randperm(nn);
        A=F(nnper(1),:);
        B=F(nnper(2),:);
        %%%%%%%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%%%%%%%%%%
        W=ceil(N/10);              %交叉点个数
        p=unidrnd(N-W+1);          %随机选择交叉范围，从p到p+W
        for i=1:W
            x=find(A==B(p+i-1));
            y=find(B==A(p+i-1));
            temp=A(p+i-1);
            A(p+i-1)=B(p+i-1); 
            B(p+i-1)=temp;
            temp=A(x); 
            A(x)=B(y); 
            B(y)=temp;
        end
        %%%%%%%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%%%%%%%
        p1=floor(1+N*rand());
        p2=floor(1+N*rand());
        while p1==p2
            p1=floor(1+N*rand());
            p2=floor(1+N*rand());
        end
        tmp=A(p1); 
        A(p1)=A(p2); 
        A(p2)=tmp;
        tmp=B(p1); 
        B(p1)=B(p2); 
        B(p2)=tmp;
        F=[F;A;B];
        [aa,bb]=size(F);
    end
    if aa>NP
        F=F(1:NP,:);             %保持种群规模为n
    end
    f=F;                         %更新种群
    f(1,:)=R;                    %保留每代最优个体
    clear F;
    gen=gen+1
    Rlength(gen)=minlen;
end
figure
for i=1:N-1
    plot([C(R(i),1),C(R(i+1),1)],[C(R(i),2),C(R(i+1),2)],'bo-');
    hold on;
end
plot([C(R(N),1),C(R(1),1)],[C(R(N),2),C(R(1),2)],'ro-');
title(['优化最短距离:',num2str(minlen)]);
figure
plot(Rlength)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')