【algorithm】算法学习----堆

堆

堆涉及到的五个问题：

• 插入一个数

• 求集合中的最小值

• 删除最小值

• 插入任意一个元素

• 删除任意一个元素

对于堆，这里需要使用树来存储。

这里以小根堆来举例：

什么是小根堆，小根堆就是父节点比其两个孩子节点都要小。

由此我们可以想到根节点就是当前堆的最小值。

堆其实是一个完全二叉树。

什么是完全二叉树？

就是除了最后一层，其余层都是满度（都是2），并且最后一层的是从左到右排列

但是如果使用节点point+value比较麻烦并且不适用于算法题里面。

所以我们使用一维数组来存储：

因此我们对于这个完全二叉树每次插入一个节点就有两个操作down()与up()操作。

要么网上调，要么往下挑。

down的逻辑：<还是以小根堆为例>

如果当前的节点比其两个孩子的节点都要大，因此将该节点与其孩子节点中最小的进行交换。

up的逻辑与：

如果当前的节点比其父亲节点要大，则交换这两个节点，一直到上升到合适的位置

因此对于开头的五个问题可以有以下解法：

假设堆为heap[N],heap数组的大小为size.

概念理解题：838. 堆排序 - AcWing题库

正式做题可能会遇到一个问题，我输入的是一个数组，我怎么把它构建成堆呢？

#include 
#include 

using namespace std;

const int N = 1e5+10;

int h[N];
int s,m,n;

void down(int u)
{
    int t=u;
    if(2*u<=s&&h[2*u]<h[t]) t=2*u;
    if(2*u+1<=s&&h[2*u+1]<h[t]) t=2*u+1;
    if(t!=u)
    {
        swap(h[t],h[u]);
        down(t);
    }
}
int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++) cin>>h[i];

    s=n;
//这里就涉及到了如何构建堆：
    for(int i=n/2;i>=1;i--) down(i);

    while(m--)
    {
        cout<<h[1]<<" ";
        h[1]=h[s];
        s--;
        down(1);
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

//Down()函数
void down(int u)
{
    int t=u;
    if(2*u<=s&&h[2*u]<h[t]) t=2*u;
    if(2*u+1<=s&&h[2*u+1]<h[t]) t=2*u+1;
    if(t!=u)
    {
        swap(h[t],h[u]);
        down(t);
    }
}
//Up()函数
void up(int u)
{
    while(u/2&&h[u/2]>h[u])
    swap(h[u/2],h[u]);
    u/=2;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

练习题：839. 模拟堆 - AcWing题库

其实我们仔细想啊，堆节点的下标我们是知道的，我们只需要一个数组存储下标为i的数是第j次插入的。但是看一下这道题目的要求：

1. I x，插入一个数 x；
2. PM，输出当前集合中的最小值；
3. DM，删除当前集合中的最小值（数据保证此时的最小值唯一）；
4. D k，删除第 k 个插入的数；
5. C k x，修改第 k 个插入的数，将其变为 x；

知道第k个插入的数我们还得找到对应数的下标，因此我们有了ph与hp这两个互指指针。

ph[k]表示第k个插入的数在数组的下标什么。

hp[k]表示堆里下标为k的点是第几个被插入的

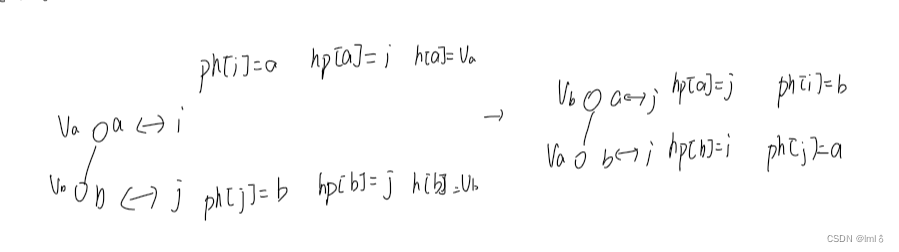
#include 
#include 
#include 

using namespace std;

const int N = 100010;

int h[N], ph[N], hp[N], cnt;

void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

int main()
{
    int n, m = 0;
    scanf("%d", &n);
    while (n -- )
    {
        char op[5];
        int k, x;
        scanf("%s", op);
        if (!strcmp(op, "I"))
        {
            scanf("%d", &x);
            cnt ++ ;
            m ++ ;
            ph[m] = cnt, hp[cnt] = m;
            h[cnt] = x;
            up(cnt);
        }
        else if (!strcmp(op, "PM")) printf("%d\n", h[1]);
        else if (!strcmp(op, "DM"))
        {
            heap_swap(1, cnt);
            cnt -- ;
            down(1);
        }
        else if (!strcmp(op, "D"))
        {
            scanf("%d", &k);
            k = ph[k];
            heap_swap(k, cnt);
            cnt -- ;
            up(k);
            down(k);
        }
        else
        {
            scanf("%d%d", &k, &x);
            k = ph[k];
            h[k] = x;
            up(k);
            down(k);
        }
    }

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

补充

strcmp()函数

该函数返回值如下：

• 如果返回值小于 0，则表示 str1 小于 str2。
• 如果返回值大于 0，则表示 str1 大于 str2。s
• 如果返回值等于 0，则表示 str1 等于 str2。