第四章 二叉树

一、树的基本术语

度：子树的个数

树的度：树中结点最大的度

根节点：一棵树可以只有一个节点

叶子结点：度为0的结点，也称为终端结点

分支结点：度不为0的结点，也称为非叶子节点或非终端结点

层数：根节点在第一层，根节点的子节点在第2层，以此类推

深度：是从根节点开始自顶向下逐层累加的

高度：是从叶结点开始自底向上逐层累加的

有序树：树中任意节点的子节点之间有顺序关系

无序树：树中任意节点的子节点之间无顺序关系

树中两个结点之间的

路径：由这两个结点之间所经过的结点序列构成

路径长度：路径上所经过的边的个数

树的家族关系

孩子：节点的子树

双亲：节点是子树的双亲

兄弟：同一个双亲的孩子之间称为兄弟

堂兄弟：双亲在同一层的节点互为堂兄弟

祖先：从根到此节点所经分支上的所有节点称为此节点的祖先

子孙：以某节点为根的子树中的任一节点都称为此节点的子孙

二、基本的二叉树

1、满二叉树

        除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。

2、完全二叉树

        一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

三、二叉树的存储结构

1、顺序存储

左孩子的地址是父母节点地址的两倍。

2、链式存储

四、二叉树的基本性质

1、树中的结点数等于所有结点的度数加1

        树中的结点总数为n，则n=分支数+1

2、非空二叉树上的叶子结点数等于度为2的结点数加1

        即n0=n2 + 1。结点总数n= n0 + n1 + n2

3、结点i的左孩子编号为2i（前提：完全二叉树）

4、非空二叉树上第k层上至多有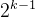个结点（k≥1）

5、高度为h的二叉树至多有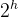-1个结点（h≥1）

6、具有n个（n>0)结点的完全二叉树的高度为[ 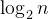]+1

二叉树的遍历

先序遍历：根左右

中序遍历：左根右

后序遍历：左右根

层序遍历：从根开始，自上而下，自左向右，一层一层遍历