• ＜排序及模拟实现＞——《Data Structure in C Train》

     目录

    详细实现链接：

    ＜排序＞《数据结构(C语言版)》

    ＜堆及堆排序＞《数据结构(C语言版)》

    1.分析实现逻辑，学习不同实现思想及写法：

    1.1插入排序（直接插入）：

    1.2 希尔排序：

    1.3 堆排序：

    1.4 直接选择排序：

    1.5 冒泡排序：

     1.6 快速排序：

    1.6.1 单趟时间复杂度：O(N)

     1.6.2 快速排序——挖坑法：

     1.6.3 快速排序——挖坑法优化（三数取中）

     1.6.4 快速排序——挖坑法优化（三数取中+小区间优化）

     1.6.5  快速排序——左右指针法

     1.6.6 快速排序——前后指针法

     1.6.7 快速排序——非递归版（排序可复用挖坑法、左右指针法、前后指针法）

     1.7 归并排序

    1.7.1   归并排序——递归版：

     1.7.2  归并排序——非递归版：

    1.8计数排序

    2. 完整源码：

    3. 各大排序性能对比分析：

    后记：●由于作者水平有限，文章难免存在谬误之处，敬请读者斧正，俚语成篇，恳望指教！

                                                                               ——By 作者：新晓·故知

    详细实现链接：

    ＜排序＞《数据结构(C语言版)》

    ＜堆及堆排序＞《数据结构(C语言版)》

    1.分析实现逻辑，学习不同实现思想及写法：

    1.1插入排序（直接插入）：

    • 时间复杂度：O(N^2)
    • 最坏情况：逆序O(N^2)
    • 最好情况：全部顺序 O(N)

    • 空间复杂度：O(1）

    • 稳定

    1.2 希尔排序：

    • 时间复杂度：O（N*logN）~ O(N^2)
    • 最好情况：O（N^1.3)
    • 最坏情况：O(N^2)
    • 空间复杂度：O(1）
    • 不稳定

    在直接插入排序的基础上优化：

    • 1.先进行预排序（分组排序），让数据接近有序
    • 2.再直接插入排序，

    多组间隔为gap的预排序，gap由大变小，

    • gap越大（以升序举例），大的数可以越快的到后面，小的数可以越快的到前面。但预排后越不接近有序
    • gap越小，越接近有序

    时间复杂度：O(N*logN)~O(N^2)

    • gap很大时，下面预排序为O(N)
    • gap很小时，数据已接近有序，近似为O(N）

     

    1.3 堆排序：

    • 时间复杂度：O（N*logN）
    • 最好情况：O（N*logN）
    • 最坏情况：O（N*logN）
    • 空间复杂度：O(1）
    • 不稳定

    给一组数据（假设存储在动态数组里），若要进行堆排序（若打印为升序），且采用向下调整，那么就把这组数据建大堆，再进行调整！然后根据下标遍历数组，即可打印为升序！

    • 大堆：堆顶数据是最大的。
    • 小堆：堆顶元素是最小的。

    建堆：

    • 倒数第一个非叶子结点（即叶子父亲的结点）开始调整。
    • 建堆的时间复杂度：O(N)

    调整方法：

    • 向上调整法：
    • 向下调整算法：
      • 前提：左右子树必须是小堆。
      • 最多调整高度次：logN次

    这里注意：

    调整分为：向上调整法、向下调整法。

    建堆分为：建大堆、建小堆。

    注意：

    若将最后的数据按照升序打印，若采用向下调整法，则选择建成大堆（只保证了父结点与子节点的相对大小，相邻没关系，这里只是建堆，而非调整后的最终形态），再从倒数第一个非叶子结点（即叶子父亲的结点）开始调整，最终调整后，再每次输出堆顶元素，打印（因为存储在数组，遍历下标打印，类似于层序遍历的操作）的就是升序！

    其实：有4种情况：

    （1）建小堆，向上调整，最终为大堆-----用于堆排降序(可以实现，但多此一举！）

    （2）建大堆，向上调整，最终为小堆-----用于堆排升序

    （3）建小堆，向下调整，最终为大堆-----用于堆排降序(可以实现，但多此一举！）

    （4）建大堆，向下调整，最终为小堆-----用于堆排升序

    在进行堆排序时，若想数据为升序，则建大堆，采用向下调整法。当把最大的换到最后，就不再将其作为接下来的调整对象。

    由于向上调整法的时间复杂度比向下调整法的时间复杂度高，因此一般采用向下调整法。

    时间复杂度：

     关于堆的选择题快速判断：

     

    （1）建小堆，向上调整，最终为大堆-----用于堆排降序(可以实现，但多此一举！）

    （2）建大堆，向上调整，最终为小堆-----用于堆排升序

    （3）建小堆，向下调整，最终为大堆-----用于堆排降序(可以实现，但多此一举！）

    （4）建大堆，向下调整，最终为小堆-----用于堆排升序

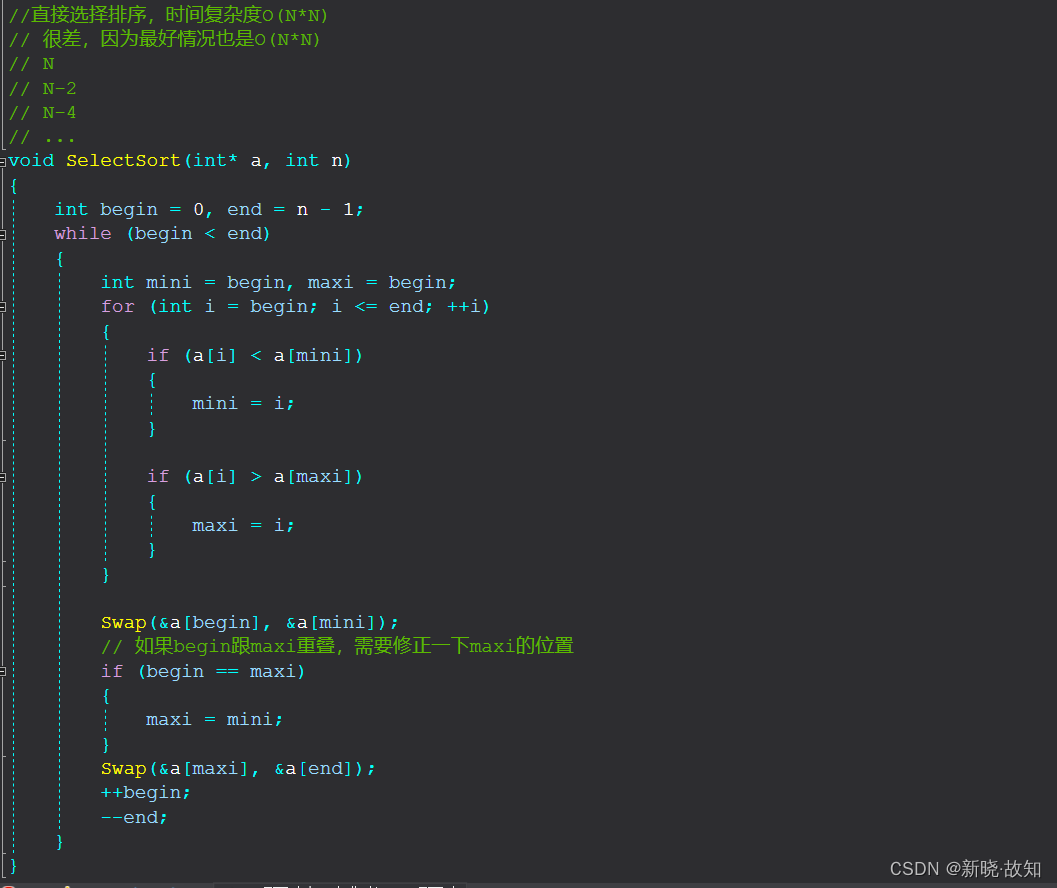
    1.4 直接选择排序：

    • 时间复杂度：O（N^2）
    • 最好情况：O（N^2）
    • 最坏情况：O（N^2）
    • 空间复杂度：O(1）
    • 不稳定

    1.5 冒泡排序：

    • 时间复杂度：O（N^2）
    • 最好情况：O（N）
    • 最坏情况：O（N^2）
    • 空间复杂度：O(1）
    • 稳定

     1.6 快速排序：

    • 时间复杂度：O（N*logN）
    • 最好情况：O（N*logN）
    • 最坏情况：O（N^2）
    • 空间复杂度：O(logN）~ O(N)
    • 不稳定

    1.6.1 单趟时间复杂度：O(N)

     1.6.2 快速排序——挖坑法：

    时间复杂度：

     

     1.6.3 快速排序——挖坑法优化（三数取中）

    时间复杂度：

     

     1.6.4 快速排序——挖坑法优化（三数取中+小区间优化）

    时间复杂度：

     

     1.6.5  快速排序——左右指针法

    时间复杂度：

     1.6.6 快速排序——前后指针法

    时间复杂度：

     

     1.6.7 快速排序——非递归版（排序可复用挖坑法、左右指针法、前后指针法）

    时间复杂度：

     

     1.7 归并排序

    • 时间复杂度：O（N*logN）
    • 最好情况：O（N*logN）
    • 最坏情况：O（N*logN）
    • 空间复杂度：O(N）
    • 稳定

    1.7.1   归并排序——递归版：

    时间复杂度：

     1.7.2  归并排序——非递归版：

    时间复杂度：

     

    1.8计数排序

    时间复杂度：O(range+N)

    空间复杂度：O（range）

     

    2. 完整源码：

    Sort.h:

    1. #pragma once
    2. #include
    3. #include
    4.  
    5. void PrintArray(int* a, int n);               //打印
    6. void InsertSort(int* a, int n);				  //插入排序
    7. void ShellSort(int* a, int n);                //希尔排序
    8. void HeapSort(int* a, int n);                 //堆排序
    9. void SelectSort(int* a, int n);               //选择排序
    10. void BubbleSort(int* a, int n);               //冒泡排序
    11. //void QuickSort(int* a, int n);              //快速排序——写法1：挖坑法(单趟分析版)
    12. void QuickSort(int* a, int left, int right);  //快速排序——写法1：挖坑法(实现排序版)
    13. void MergeSort(int* a, int n);                //归并排序
    14. void QuickSortNonR(int* a, int n);			  //快速排序（非递归版）
    15. void MergeSortNonR(int* a, int n);            //归并排序（非递归版）
    16. void CountSort(int* a, int n);                //计数排序

    Sort.c:

    1. #include"Sort.h"
    2. #include"Stack.h"
    3. //这里采用升序讲解
    4. //打印
    5. void PrintArray(int* a, int n)
    6. {
    7. 	for (int i = 0; i < n; i++)
    8. 	{
    9. 		printf("%d ", a[i]);
    10. 	}
    11. 	printf("\n");
    12. }
    13. ///
    14. //插入排序
    15. //时间复杂度：O(N^2)
    16. //最坏情况：逆序
    17. //最好情况：全部顺序 O(N)
    18. void InsertSort(int* a, int n)
    19. {
    20. 	//假设[0,end]有序，将end+1位置的值插入进去，让[0,end+1]有序
    21. 	for (int i = 0; i < n - 1; i++)
    22. 	{
    23. 		int end = i;
    24. 		int tmp = a[end + 1];
    25. 		while (end >= 0)
    26. 		{
    27. 			if (a[end] > tmp)  //升序
    28. 			//if (a[end] < tmp)  //降序
    29. 			{
    30. 				a[end + 1] = a[end];
    31. 				--end;
    32. 			}
    33. 			else
    34. 			{
    35. 				break;
    36. 			}
    37. 		}
    38. 		a[end + 1] = tmp;
    39. 	}
    40. }
    41. //
    42. //希尔排序
    43. //在直接插入排序的基础上优化
    44. //1.先进行预排序（分组排序），让数据接近有序
    45. //2.再直接插入排序，
    46. //多组间隔为gap的预排序，gap由大变小，
    47. //gap越大（以升序举例），大的数可以越快的到后面，小的数可以越快的到前面。但预排后越不接近有序
    48. //gap越小，越接近有序
    49. //时间复杂度：O(logN*N)或者O(log3N*N)
    50. //gap很大时，下面预排序为O(N)
    51. //gap很小时，数据已接近有序，近似为ON）
    52. //平均时间复杂度：O（N^1.3)
    53. void ShellSort(int* a, int n)
    54. {
    55. 	int gap = n;  //可以自行设置，但不会给固定的值
    56. 	//把间隔为gap的多组数据同时排序（注意：理解这个多组的含义）
    57. 	//end最终位置：n-gap-1
    58. 	//gap的设置方式之一：
    59. 	while(gap > 1)
    60. 	{
    61. 		//gap=gap/2;        //一定会保证最后一次为1    //运行了logN次
    62. 		gap = gap / 3 + 1;  //但要保证最后一次为1      //运行了log3N次
    63. 		//gap>1时都是预排序，排序后接近有序
    64. 		//gap==1时，就是直接插入排序
    65. 		
    66. 		for (int i = 0; i < n - gap; i++)
    67. 		{
    68. 			int end = i;
    69. 			int tmp = a[end + gap];
    70. 			while (end >= 0)
    71. 			{
    72. 				if (a[end] > tmp)
    73. 				{
    74. 					a[end + gap] = a[end];
    75. 					end -= gap;
    76. 				}
    77. 				else
    78. 				{
    79. 					break;
    80. 				}
    81. 			}
    82. 			a[end + gap] = tmp;
    83. 		}
    84. 	}
    85.  
    86. }
    87.  
    88. /
    89. //堆排序
    90. void Swap(int* p1, int* p2)
    91. {
    92. 	int tmp = *p1;
    93. 	*p1 = *p2;
    94. 	*p2 = tmp;
    95. }
    96. //（1）建小堆，向上调整，最终为大堆---- - 用于堆排降序
    97. //（2）建大堆，向上调整，最终为小堆---- - 用于堆排升序
    98. //（3）建小堆，向下调整，最终为大堆---- - 用于堆排降序（可以实现，多此一举）
    99. //（4）建大堆，向下调整，最终为小堆---- - 用于堆排升序
    100. //注：由于向上调整法的时间复杂度比向下调整法的时间复杂度高，因此一般采用向下调整法。
    101. //堆排序，采用数组存储，操作下标。但逻辑要是二叉树
    102. //把数据建成堆
    103. //1.堆排序调整-向下调整法
    104. void AdjustDwon(int* a, int n, int root)
    105. {
    106. 	int parent = root;
    107. 	int child = parent * 2 + 1; // 默认是左孩子
    108. 	//1.建大堆，再调整
    109. 	while (child < n)
    110. 	{
    111. 		// 1、选出左右孩子中大的那一个
    112. 		if (child + 1 < n && a[child + 1] > a[child])
    113. 		{
    114. 			child += 1;
    115. 		}
    116.  
    117. 		if (a[child] > a[parent])
    118. 		{
    119. 			Swap(&a[child], &a[parent]);
    120. 			parent = child;
    121. 			child = parent * 2 + 1;
    122. 		}
    123. 		else
    124. 		{
    125. 			break;
    126. 		}
    127. 	}
    128. 	2.建小堆，再调整
    129. 	//while (child < n)
    130. 	//{
    131. 	//	// 1、选出左右孩子中小的那一个
    132. 	//	if (child + 1 < n && a[child + 1] < a[child])
    133. 	//	{
    134. 	//		child += 1;
    135. 	//	}
    136.  
    137. 	//	if (a[child] < a[parent])
    138. 	//	{
    139. 	//		Swap(&a[child], &a[parent]);
    140. 	//		parent = child;
    141. 	//		child = parent * 2 + 1;
    142. 	//	}
    143. 	//	else
    144. 	//	{
    145. 	//		break;
    146. 	//	}
    147. 	//}
    148. }
    149. //2.堆排序调整-向上调整法
    150. void AdjustUp(int* a, int child)
    151. {
    152. 	int parent = (child - 1) / 2;
    153. 	//1.建大堆，再调整
    154. 	while (child > 0)
    155. 	{
    156. 		if (a[child] > a[parent])
    157. 		{
    158. 			Swap(&a[child], &a[parent]);
    159. 			child = parent;
    160. 			parent = (child - 1) / 2;
    161. 		}
    162. 		else
    163. 		{
    164. 			break;
    165. 		}
    166. 	}
    167. 	2.建小堆，再调整
    168. 	//while (child > 0)
    169. 	//{
    170. 	//	if (a[child] < a[parent])
    171. 	//	{
    172. 	//		Swap(&a[child], &a[parent]);
    173. 	//		child = parent;
    174. 	//		parent = (child - 1) / 2;
    175. 	//	}
    176. 	//	else
    177. 	//	{
    178. 	//		break;
    179. 	//	}
    180. 	//}
    181. }
    182.  
    183. //堆排序（建堆）
    184. // 升序，建小堆？还是大堆？  -> 大堆
    185. // 建堆只是第一步，并非最终形态，还要进行调整（一般选择向下调整）
    186. // 整体时间复杂度O(N*logN)
    187. void HeapSort(int* a, int n)
    188. {
    189. 	// 建堆  时间复杂度：O(N)
    190. 	//调整
    191. 	1.向上调整法
    192. 	//for (int i = 1; i < n; ++i)
    193. 	//{
    194. 	//	AdjustUp(a, i);
    195. 	//}
    196. 	//2.向下调整法
    197. 	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
    198. 	{
    199. 		AdjustDwon(a, n, i);
    200. 	}
    201.  
    202. 	// 排升序，采用向下调整法，那么，建大堆还是小堆？ -->建大堆
    203. 	int end = n - 1;
    204. 	while (end > 0)
    205. 	{
    206. 		Swap(&a[0], &a[end]);
    207. 		AdjustDwon(a, end, 0);
    208. 		--end;
    209. 	}
    210. }
    211. /
    212. //直接选择排序，时间复杂度O(N*N)
    213. // 很差，因为最好情况也是O(N*N)
    214. // N
    215. // N-2
    216. // N-4
    217. // ...
    218. void SelectSort(int* a, int n)
    219. {
    220. 	int begin = 0, end = n - 1;
    221. 	while (begin < end)
    222. 	{
    223. 		int mini = begin, maxi = begin;
    224. 		for (int i = begin; i <= end; ++i)
    225. 		{
    226. 			if (a[i] < a[mini])
    227. 			{
    228. 				mini = i;
    229. 			}
    230.  
    231. 			if (a[i] > a[maxi])
    232. 			{
    233. 				maxi = i;
    234. 			}
    235. 		}
    236.  
    237. 		Swap(&a[begin], &a[mini]);
    238. 		// 如果begin跟maxi重叠，需要修正一下maxi的位置
    239. 		if (begin == maxi)
    240. 		{
    241. 			maxi = mini;
    242. 		}
    243. 		Swap(&a[maxi], &a[end]);
    244. 		++begin;
    245. 		--end;
    246. 	}
    247. }
    248. /
    249. //冒泡排序
    250. // 时间复杂度：O（N*N）
    251. // 最好情况:O(N)
    252. // N-1
    253. // N-2
    254. // ...
    255. // 跟直接插入排序相比？谁更好 -> 直接插排序入更好
    256.  
    257. void BubbleSort(int* a, int n)
    258. {
    259. 	//写法1：
    260. 	for (int j = 0; j < n; ++j)
    261. 	{
    262. 		int exchange = 0;
    263. 		for (int i = 1; i < n - j; ++i)
    264. 		{
    265. 			if (a[i - 1] > a[i])
    266. 			{
    267. 				Swap(&a[i - 1], &a[i]);
    268. 				exchange = 1;
    269. 			}
    270. 		}
    271.  
    272. 		if (exchange == 0)
    273. 		{
    274. 			break;
    275. 		}
    276. 	}
    277. 	写法2：
    278. 	//int end = n;
    279. 	//while (end > 0)
    280. 	//{
    281. 	//	for (int i = 1; i < end; ++i)
    282. 	//	{
    283. 	//		if (a[i - 1] > a[i])
    284. 	//		{
    285. 	//			Swap(&a[i - 1], &a[i]);
    286. 	//		}
    287. 	//	}
    288. 	//	--end;
    289. 	//}
    290. }
    291. /
    292. 快速排序——写法1：挖坑法(单趟分析版)       
    293.  单趟排序时间复杂度：O(N)
    294. //void QuickSort(int* a, int n)    
    295. //{
    296. //	int begin = 0, end = n - 1;
    297. //	int pivot = begin;
    298. //	int key = a[begin];  //指定了第一次关键字为begin
    299. //
    300. //	while (begin < end)
    301. //	{
    302. //		//右边找小，放到左边
    303. //		while (begin < end && a[end] >= key)
    304. //		{
    305. //			--end;
    306. //		}
    307. //		//小的放到左边的坑里，自己形成新的坑位
    308. //		a[pivot] = a[end];
    309. //		pivot = end;
    310. //		//左边找大
    311. //		while (begin < end && a[begin] <= key)
    312. //		{
    313. //			++begin;
    314. //		}
    315. //		//大的放到左边的坑里，自己形成新的坑位
    316. //		a[pivot] = a[begin];
    317. //		pivot = begin;
    318. //
    319. //	}
    320. //	pivot = begin;
    321. //	a[pivot] = key;
    322. //}
    323. 快速排序——写法1：挖坑法(实现排序版)
    324. 时间复杂度：
    325. 最坏情况：有序-->O O(N^2) ，性能相当于插入排序。  解决：“三数取中法”，使其取得key不是最大或最小
    326. //void QuickSort(int* a, int left, int right)
    327. //{
    328. //	if (left >= right)
    329. //		return;
    330. //	int begin = left, end = right;
    331. //	int pivot = begin;
    332. //	int key = a[begin];  //指定了第一次关键字为begin
    333. //
    334. //	while (begin < end)   //单趟排序
    335. //	{
    336. //		//右边找小，放到左边
    337. //		while (begin < end && a[end] >= key)
    338. //		{
    339. //			--end;
    340. //		}
    341. //		//小的放到左边的坑里，自己形成新的坑位
    342. //		a[pivot] = a[end];
    343. //		pivot = end;
    344. //		//左边找大
    345. //		while (begin < end && a[begin] <= key)
    346. //		{
    347. //			++begin;
    348. //		}
    349. //		//大的放到左边的坑里，自己形成新的坑位
    350. //		a[pivot] = a[begin];
    351. //		pivot = begin;
    352. //
    353. //	}
    354. //	pivot = begin;
    355. //	a[pivot] = key;
    356. //
    357. //	// [left, right]
    358. //	// [left, pivot-1] pivot [pivot+1, right]	
    359. //	// 左子区间和右子区间有序，我们就有序了，如果让他们有序呢？ 分治递归
    360. //	QuickSort(a, left, pivot - 1);
    361. //	QuickSort(a, pivot + 1, right);
    362. //}
    363. //
    364. 快速排序——写法2：挖坑法优化--->（三数取中，解决原始数据有序情况）
    365.  三数取中
    366. //int GetMidIndex(int* a, int left, int right)
    367. //{
    368. //	int mid = (left + right) >> 1;
    369. //	if (a[left] < a[mid])
    370. //	{
    371. //		if (a[mid] < a[right])
    372. //		{
    373. //			return mid;
    374. //		}
    375. //		else if (a[left] > a[right])
    376. //		{
    377. //			return left;
    378. //		}
    379. //		else
    380. //		{
    381. //			return right;
    382. //		}
    383. //	}
    384. //	else // a[left] > a[mid]
    385. //	{
    386. //		if (a[mid] > a[right])
    387. //		{
    388. //			return mid;
    389. //		}
    390. //		else if (a[left] < a[right])
    391. //		{
    392. //			return left;
    393. //		}
    394. //		else
    395. //		{
    396. //			return right;
    397. //		}
    398. //	}
    399. //}
    400. //void QuickSort(int* a, int left, int right)
    401. //{
    402. //	if (left >= right)
    403. //		return;
    404. //	int keyIndex = GetMidIndex(a, left, right);  //三数取中，解决原始数据有序的性能下降
    405. //	Swap(&a[left], &a[keyIndex]);
    406. //
    407. //	int begin = left, end = right;
    408. //	int pivot = begin;
    409. //	int key = a[begin];
    410. //
    411. //	while (begin < end)  //单趟排序  O（N）
    412. //	{
    413. //		// 右边找小，放到左边
    414. //		while (begin < end && a[end] >= key)
    415. //			--end;
    416. //
    417. //		// 小的放到左边的坑里，自己形成新的坑位
    418. //		a[pivot] = a[end];
    419. //		pivot = end;
    420. //
    421. //		// 左边找大
    422. //		while (begin < end && a[begin] <= key)
    423. //			++begin;
    424. //
    425. //		// 大的放到左边的坑里，自己形成新的坑位
    426. //		a[pivot] = a[begin];
    427. //		pivot = begin;
    428. //	}
    429. //
    430. //	pivot = begin;
    431. //	a[pivot] = key;
    432. //
    433. //	// [left, right]
    434. //	// [left, pivot-1] pivot [pivot+1, right]	
    435. //	// 左子区间和右子区间有序，我们就有序了，如果让他们有序呢？ 分治递归
    436. //	QuickSort(a, left, pivot - 1);
    437. //	QuickSort(a, pivot + 1, right);
    438. //}
    440. 快速排序——写法3：挖坑法优化--->（三数取中，解决原始数据有序情况）,再根据处理量分情况排序（小区间优化）
    441.  三数取中
    442. //int GetMidIndex(int* a, int left, int right)
    443. //{
    444. //	int mid = (left + right) >> 1;
    445. //	if (a[left] < a[mid])
    446. //	{
    447. //		if (a[mid] < a[right])
    448. //		{
    449. //			return mid;
    450. //		}
    451. //		else if (a[left] > a[right])
    452. //		{
    453. //			return left;
    454. //		}
    455. //		else
    456. //		{
    457. //			return right;
    458. //		}
    459. //	}
    460. //	else // a[left] > a[mid]
    461. //	{
    462. //		if (a[mid] > a[right])
    463. //		{
    464. //			return mid;
    465. //		}
    466. //		else if (a[left] < a[right])
    467. //		{
    468. //			return left;
    469. //		}
    470. //		else
    471. //		{
    472. //			return right;
    473. //		}
    474. //	}
    475. //}
    476. //void QuickSort(int* a, int left, int right)
    477. //{
    478. //	if (left >= right)
    479. //		return;
    480. //	int keyIndex = GetMidIndex(a, left, right);
    481. //	Swap(&a[left], &a[keyIndex]);
    482. //
    483. //	int begin = left, end = right;
    484. //	int pivot = begin;
    485. //	int key = a[begin];
    486. //
    487. //	// O（N）
    488. //	while (begin < end)
    489. //	{
    490. //		// 右边找小，放到左边
    491. //		while (begin < end && a[end] >= key)
    492. //			--end;
    493. //
    494. //		// 小的放到左边的坑里，自己形成新的坑位
    495. //		a[pivot] = a[end];
    496. //		pivot = end;
    497. //
    498. //		// 左边找大
    499. //		while (begin < end && a[begin] <= key)
    500. //			++begin;
    501. //
    502. //		// 大的放到左边的坑里，自己形成新的坑位
    503. //		a[pivot] = a[begin];
    504. //		pivot = begin;
    505. //	}
    506. //
    507. //	pivot = begin;
    508. //	a[pivot] = key;
    509. //
    510. //	// 小区间优化
    511. //	//这个值会随原始数据量改变，而官方给13左右
    512. //	if (pivot - 1 - left > 10)   //官方给13左右
    513. //	{
    514. //		QuickSort(a, left, pivot - 1);
    515. //	}
    516. //	else
    517. //	{
    518. //		//InsertSort(int* a, int n)
    519. //		InsertSort(a + left, pivot - 1 - left + 1);  //left不一定从0开始，传数据个数
    520. //	}
    521. //
    522. //	if (right - (pivot + 1) > 10)
    523. //	{
    524. //		QuickSort(a, pivot + 1, right);
    525. //	}
    526. //	else
    527. //	{
    528. //		InsertSort(a + pivot + 1, right - (pivot + 1) + 1);
    529. //	}
    530. //}
    532. 快速排序——写法4：左右指针法：找小找大交换
    533.  三数取中
    534. //int GetMidIndex(int* a, int left, int right)
    535. //{
    536. //	int mid = (left + right) >> 1;
    537. //	if (a[left] < a[mid])
    538. //	{
    539. //		if (a[mid] < a[right])
    540. //		{
    541. //			return mid;
    542. //		}
    543. //		else if (a[left] > a[right])
    544. //		{
    545. //			return left;
    546. //		}
    547. //		else
    548. //		{
    549. //			return right;
    550. //		}
    551. //	}
    552. //	else // a[left] > a[mid]
    553. //	{
    554. //		if (a[mid] > a[right])
    555. //		{
    556. //			return mid;
    557. //		}
    558. //		else if (a[left] < a[right])
    559. //		{
    560. //			return left;
    561. //		}
    562. //		else
    563. //		{
    564. //			return right;
    565. //		}
    566. //	}
    567. //}
    568. 左右指针法：找小找大交换
    569. //void QuickSort(int* a, int left, int right)
    570. //{
    571. //	if (left >= right)
    572. //		return;
    573. //
    574. //	int index = GetMidIndex(a, left, right);
    575. //	Swap(&a[left], &a[index]);
    576. //
    577. //	int begin = left, end = right;
    578. //	int keyi = begin;
    579. //
    580. //	while (begin < end)
    581. //	{
    582. //		// 找小
    583. //		while (begin < end && a[end] >= a[keyi])
    584. //		{
    585. //			--end;
    586. //		}
    587. //
    588. //		// 找大
    589. //		while (begin < end && a[begin] <= a[keyi])
    590. //		{
    591. //			++begin;
    592. //		}
    593. //
    594. //		Swap(&a[begin], &a[end]);
    595. //	}
    596. //
    597. //	Swap(&a[begin], &a[keyi]);
    598. //	int key = begin;
    599. //
    600. //	// 小区间优化
    601. //	//这个值会随原始数据量改变，而官方给13左右
    602. //	if (key - 1 - left > 10)   //官方给13左右
    603. //	{
    604. //		QuickSort(a, left, key - 1);
    605. //	}
    606. //	else
    607. //	{
    608. //		//InsertSort(int* a, int n)
    609. //		InsertSort(a + left, key - 1 - left + 1);  //left不一定从0开始，传数据个数
    610. //	}
    611. //
    612. //	if (right - (key + 1) > 10)
    613. //	{
    614. //		QuickSort(a, key + 1, right);
    615. //	}
    616. //	else
    617. //	{
    618. //		InsertSort(a + key + 1, right - (key + 1) + 1);
    619. //	}
    620. //}
    622. //快速排序——写法5：前后指针法：cur找小，每次找到比keyi小额值，就++prev，然后交换prev与cur的位置交换
    623. //1.会有自己与自己交换的情况，2.也有异步交换，3.最后实现左边全为小于key,右边全为大于key
    624. // 三数取中
    625. int GetMidIndex(int* a, int left, int right)
    626. {
    627. 	int mid = (left + right) >> 1;
    628. 	if (a[left] < a[mid])
    629. 	{
    630. 		if (a[mid] < a[right])
    631. 		{
    632. 			return mid;
    633. 		}
    634. 		else if (a[left] > a[right])
    635. 		{
    636. 			return left;
    637. 		}
    638. 		else
    639. 		{
    640. 			return right;
    641. 		}
    642. 	}
    643. 	else // a[left] > a[mid]
    644. 	{
    645. 		if (a[mid] > a[right])
    646. 		{
    647. 			return mid;
    648. 		}
    649. 		else if (a[left] < a[right])
    650. 		{
    651. 			return left;
    652. 		}
    653. 		else
    654. 		{
    655. 			return right;
    656. 		}
    657. 	}
    658. }
    659. //前后指针法
    660. void QuickSort(int* a, int left, int right)
    661. {
    662. 	if (left >= right)
    663. 		return;
    664.  
    665. 	int index = GetMidIndex(a, left, right);
    666. 	Swap(&a[left], &a[index]);
    667.  
    668. 	int keyi = left;
    669. 	int prev = left, cur = left + 1;
    670. 	while (cur <= right)
    671. 	{
    672. 		if (a[cur] < a[keyi]
    673. 			&& ++prev != cur)   //++prev != cur：优化自己与自己交换的情况
    674. 		{
    675. 			Swap(&a[prev], &a[cur]);
    676. 		}
    677.  
    678. 		++cur;
    679. 	}
    680.  
    681. 	Swap(&a[keyi], &a[prev]);
    682.  
    683. 	int key = prev;
    684. 	// 小区间优化
    685. 	//这个值会随原始数据量改变，而官方给13左右
    686. 	if (key - 1 - left > 10)   //官方给13左右
    687. 	{
    688. 		QuickSort(a, left, key - 1);
    689. 	}
    690. 	else
    691. 	{
    692. 		//InsertSort(int* a, int n)
    693. 		InsertSort(a + left, key - 1 - left + 1);  //left不一定从0开始，传数据个数
    694. 	}
    695.  
    696. 	if (right - (key + 1) > 10)
    697. 	{
    698. 		QuickSort(a, key + 1, right);
    699. 	}
    700. 	else
    701. 	{
    702. 		InsertSort(a + key + 1, right - (key + 1) + 1);
    703. 	}
    704. }
    705.  
    706. //递归的缺陷：若递归的深度太深，程序没错，但是栈的空间不够用，会导致溢出
    707. //递归改非递归：方法1：（简单的）可以直接改循环 2.（复杂一点）使用数据结构的栈进行模拟递归过程
    708. //快速排序——非递归版
    709. //（复杂一点）使用数据结构的栈进行模拟递归过程：不会再有栈溢出问题，也会有空间消耗
    710. //但数据结构中的栈是malloc出来的，开辟在堆（操作系统对内存的划分），而堆的空间比栈大
    711. void QuickSortNonR(int* a, int n)
    712. {
    713. 	ST st;
    714. 	StackInit(&st);
    715. 	StackPush(&st, n - 1);
    716. 	StackPush(&st, 0);
    717. 	while (!StackEmpty(&st))
    718. 	{
    719. 		int left = StackTop(&st);
    720. 		StackPop(&st);
    721. 		int right = StackTop(&st);
    722. 		StackPop(&st);
    723. 		//调用单趟排序
    724. 		int index = GetMidIndex(a, left, right);
    725. 		//Swap(&a[left], &a[index]);
    726.  
    727. 		int keyi = left;
    728. 		int prev = left, cur = left + 1;
    729. 		while (cur <= right)
    730. 		{
    731. 			if (a[cur] < a[keyi]
    732. 				&& ++prev != cur)   //++prev != cur：优化自己与自己交换的情况
    733. 			{
    734. 				Swap(&a[prev], &a[cur]);
    735. 			}
    736.  
    737. 			++cur;
    738. 		}
    739.  
    740. 		Swap(&a[keyi], &a[prev]);
    741. 		int keyIndex = prev;
    742.  
    743. 		//栈里面的就需要单趟分割排序
    744. 		//[left,keyIndex-1] keyIndex [keyIndex+1,right]
    745. 		if (keyIndex + 1 < right)
    746. 		{
    747. 			StackPush(&st, right);
    748. 			StackPush(&st, keyIndex+1);
    749.  
    750. 		}
    751. 		if (left < keyIndex - 1)
    752. 		{
    753. 			StackPush(&st, keyIndex - 1);
    754. 			StackPush(&st, left);
    755. 		}
    756. 	}
    757. 	StackDestory(&st);
    758.  
    759. }
    760. ///
    761. //归并排序
    762. //1.假设左半区间、右半区间有序，依次对比取小的放到新的临时数组
    763. //2.若左半区间、右半区间没有序，则递归进行
    764. void _MergeSort(int* a, int left, int right, int* tmp)
    765. {
    766. 	if (left >= right)
    767. 		return;
    768.  
    769. 	int mid = (left + right) >> 1;
    770. 	//假设 [left, mid] [mid+1, right]有序，那么我们就可以归并了
    771. 	_MergeSort(a, left, mid, tmp);
    772. 	_MergeSort(a, mid + 1, right, tmp);
    773.  
    774. 	// 归并
    775. 	int begin1 = left, end1 = mid;
    776. 	int begin2 = mid + 1, end2 = right;
    777. 	int index = left;
    778. 	while (begin1 <= end1 && begin2 <= end2)
    779. 	{
    780. 		if (a[begin1] < a[begin2])
    781. 		{
    782. 			tmp[index++] = a[begin1++];
    783. 		}
    784. 		else
    785. 		{
    786. 			tmp[index++] = a[begin2++];
    787. 		}
    788. 	}
    789.  
    790. 	while (begin1 <= end1)
    791. 	{
    792. 		tmp[index++] = a[begin1++];
    793. 	}
    794.  
    795. 	while (begin2 <= end2)
    796. 	{
    797. 		tmp[index++] = a[begin2++];
    798. 	}
    799.  
    800. 	// 拷贝回去
    801. 	for (int i = left; i <= right; ++i)
    802. 	{
    803. 		a[i] = tmp[i];
    804. 	}
    805. }
    806.  
    807. void MergeSort(int* a, int n)
    808. {
    809. 	int* tmp = (int*)malloc(sizeof(int) * n); //空间复杂度为O(N)
    810. 	_MergeSort(a, 0, n - 1, tmp);
    811. 	free(tmp);
    812. }
    813. //归并排序——非递归版
    814. //（复杂一点）使用数据结构的栈进行模拟递归过程
    815. //归并排序的非递归：先相邻两两归并，再四四归并，依次扩大
    816. void MergeSortNonR(int* a, int n)
    817. {
    818. 	int* tmp = (int*)malloc(sizeof(int) * n);
    819. 	int gap = 1;  //每组数据个数
    820. 	while (gap < n)
    821. 	{
    822. 		for (int i = 0; i < n; i += 2 * gap)
    823. 		{
    824. 			//[i,i+gap-1] [i+gap,i+2*gap-1]
    825.  
    826. 			// 归并
    827. 			int begin1 = i, end1 = i + gap - 1;
    828. 			int begin2 = i + gap, end2 = i + 2 * gap - 1;
    829. 			//归并过程中右半区间可能就不存在
    830. 			if (begin2 >= n)
    831. 				break;
    832. 			//归并过程中右半区间算多了,修正
    833. 			if (end2 >= n)
    834. 			{
    835. 				end2 = n - 1;
    836. 			}
    837. 			int index = i;
    838. 			while (begin1 <= end1 && begin2 <= end2)
    839. 			{
    840. 				if (a[begin1] < a[begin2])
    841. 				{
    842. 					tmp[index++] = a[begin1++];
    843. 				}
    844. 				else
    845. 				{
    846. 					tmp[index++] = a[begin2++];
    847. 				}
    848. 			}
    849.  
    850. 			while (begin1 <= end1)
    851. 			{
    852. 				tmp[index++] = a[begin1++];
    853. 			}
    854.  
    855. 			while (begin2 <= end2)
    856. 			{
    857. 				tmp[index++] = a[begin2++];
    858. 			}
    859. 			// 拷贝回去
    860. 			for (int j = i; j < end2; ++j)
    861. 			{
    862. 				a[j] = tmp[j];
    863. 			}
    864. 		}
    865. 		gap *= 2;
    866. 	}
    867. 	free(tmp);
    868. }
    869. //归并排序，也叫外排序，还可以对文件中数据进行排序
    870. //假设10G的数据放到硬盘中，要排序可能内存不够，假设有1G内存可以用，如何排序？
    871. //依次读文件，每次读1G到内存中放到一个数组，用快排对其进行排序，再写到一个文件，2G、4G、8G归并需要借助在磁盘归并
    872. //磁盘只能依次读数据
    873.  
    874. //非比较排序
    875. //
    876. //基数排序（桶排序）实际中运用少，只对整数排序
    877. //
    878. //计数排序
    879. //统计数据个数，不进行比较
    880. //时间复杂度：O(range+N)
    881. //空间复杂度：O(range)
    882. //说明计数排序适用于范围集中的数据
    883. //使用相对映射，也可对负数进行排序
    884. //字符串、浮点数等等不行
    885. void CountSort(int* a, int n)
    886. {
    887. 	int min = a[0], max = a[0];
    888. 	for (int i = 1; i < n; ++i)
    889. 	{
    890. 		if (a[i] < min)
    891. 			min = a[i];
    892. 		if (a[i] > max)
    893. 			max = a[i];
    894. 	}
    895.  
    896. 	int range = max - min + 1;
    897. 	int* countA = (int*)malloc(sizeof(int) * range);
    898. 	assert(countA);
    899.  
    900. 	memset(countA, 0, sizeof(int) * range);
    901. 	//计数
    902. 	for (int i = 0; i < n; ++i)
    903. 		countA[a[i] - min]++;
    904. 	//排序
    905. 	int j = 0;
    906. 	for (int i = 0; i < range; ++i)
    907. 	{
    908. 		while (countA[i]--)
    909. 		{
    910. 			a[j++] = i + min;
    911. 		}
    912. 	}
    913. }

    Test.c:

    1. #include"Sort.h"
    2. #include"Stack.h"
    3.  
    4. void TestInsertSort()
    5. {
    6. 	int a[] = { 3, 5, 2, 7, 8, 6, 1, 9, 4, 0 };
    7. 	PrintArray(a, sizeof(a) / sizeof(int));
    8. 	InsertSort(a, sizeof(a) / sizeof(int));
    9. 	PrintArray(a, sizeof(a) / sizeof(int));
    10. }
    11. void TestShellSort()
    12. {
    13. 	int a[] = { 3, 5, 2, 7, 8, 6, 1, 9, 4, 0 };
    14. 	PrintArray(a, sizeof(a) / sizeof(int));
    15. 	ShellSort(a, sizeof(a) / sizeof(int));
    16. 	PrintArray(a, sizeof(a) / sizeof(int));
    17. }
    18. void TestHeapSort()
    19. {
    20. 	int a[] = { 3, 5, 2, 7, 8, 6, 1, 9, 4, 0 }; 
    21. 	PrintArray(a, sizeof(a) / sizeof(int));
    22. 	HeapSort(a, sizeof(a) / sizeof(int));
    23. 	PrintArray(a, sizeof(a) / sizeof(int));
    24. }
    25. void TestSelectSort()
    26. {
    27. 	int a[] = { 9, 3, 5, 2, 7, 8, 6, -1, 9, 4, 0 };
    28. 	PrintArray(a, sizeof(a) / sizeof(int));
    29. 	SelectSort(a, sizeof(a) / sizeof(int));
    30. 	PrintArray(a, sizeof(a) / sizeof(int));
    31. }
    32. void TestBubbleSort()
    33. {
    34. 	int a[] = { 9, 3, 5, 2, 7, 8, 6, -1, 9, 4, 0 };
    35. 	PrintArray(a, sizeof(a) / sizeof(int));
    36. 	BubbleSort(a, sizeof(a) / sizeof(int));
    37. 	PrintArray(a, sizeof(a) / sizeof(int));
    38. }
    39. void TestQuickSort()
    40. {
    41. 	int a[] = { 6, 3, 5, 2, 7, 8, 9, 4, 1 };
    42. 	//int a[] = { 49, 38, 65, 97, 76, 13, 27, 49};
    43. 	//int a[] = { 49, 38, 65, 97, 76, 13, 27, 49, 13, 27, 49 };
    44. 	PrintArray(a, sizeof(a) / sizeof(int));
    45. 	//QuickSort(a, sizeof(a) / sizeof(int) );    //快速排序——写法1：挖坑法(单趟分析版)
    46. 	QuickSort(a, 0, sizeof(a) / sizeof(int)-1);  //快速排序——写法1：挖坑法(实现排序版)
    47. 	PrintArray(a, sizeof(a) / sizeof(int));
    48. }
    49. void TestMergeSort()
    50. {
    51. 	//int a[] = { 10, 6, 7 ,1, 3, 9, 4, 2 };
    52. 	int a[] = { 49, 38, 65, 97, 76, 13, 27, 49, 13, 27, 49 };
    53. 	PrintArray(a, sizeof(a) / sizeof(int));
    54. 	MergeSort(a, sizeof(a) / sizeof(int));
    55. 	PrintArray(a, sizeof(a) / sizeof(int));
    56. }
    57. void TestQuickSortNonR()
    58. {
    59. 	//int a[] = { 6, 3, 5, 2, 7, 8, 9, 4, 1 };
    60. 	//int a[] = { 49, 38, 65, 97, 76, 13, 27, 49};
    61. 	int a[] = { 49, 38, 65, 97, 76, 13, 27, 49, 13, 27, 49 };
    62. 	PrintArray(a, sizeof(a) / sizeof(int));
    63. 	QuickSortNonR(a, sizeof(a) / sizeof(int));
    64. 	PrintArray(a, sizeof(a) / sizeof(int));
    65. }
    66. void TestMergeSortNonR()
    67. {
    68. 	//int a[] = { 10, 6, 7 ,1, 3, 9, 4, 2 };
    69. 	int a[] = { 49, 38, 65, 97, 76, 13, 27, 49, 13, 27, 49 };
    70. 	PrintArray(a, sizeof(a) / sizeof(int));
    71. 	MergeSortNonR(a, sizeof(a) / sizeof(int));
    72. 	PrintArray(a, sizeof(a) / sizeof(int));
    73. }
    74. void TestCountSort()
    75. {
    76. 	//int a[] = { 10, 6, 7 ,1, 3, 9, 4, 2 };
    77. 	int a[] = { 49, 38, 65, 97, 76, 13, 27, 49, 13, 27, 49 };
    78. 	PrintArray(a, sizeof(a) / sizeof(int));
    79. 	CountSort(a, sizeof(a) / sizeof(int));
    80. 	PrintArray(a, sizeof(a) / sizeof(int));
    81. }
    82. int main()
    83. {
    84. 	//TestInsertSort();
    85. 	//TestShellSort();
    86. 	//TestHeapSort();
    87. 	//TestSelectSort();
    88. 	//TestBubbleSort();
    89. 	//TestQuickSort();
    90. 	//TestMergeSort();
    91. 	//TestQuickSortNonR();
    92. 	//TestMergeSortNonR();
    93. 	TestCountSort();
    94. 	return 0;
    95. }

     注：

    由于这里的快速排序——非递归版，使用数据结构的栈进行模拟递归过程。因此要附用栈的实现代码。这里将栈的代码给出，使用时包含头文件，再复用即可！

    Stack.h:

    1. #pragma once
    2.  
    3. #include 
    4. #include 
    5. #include 
    6. #include 
    7.  
    8. typedef char STDataType;
    9.  
    10. typedef struct Stack
    11. {
    12. 	STDataType* a;   //通过数组实现栈的结构
    13. 	int top;
    14. 	int capacity;
    15. }ST;
    16. //初始化
    17. void StackInit(ST* ps);
    18. //释放内存、销毁空间
    19. void StackDestory(ST* ps);
    20. // 入栈
    21. void StackPush(ST* ps, STDataType x);
    22. // 出栈
    23. void StackPop(ST* ps);
    24. //取栈顶数据
    25. STDataType StackTop(ST* ps);
    26. //栈的大小
    27. int StackSize(ST* ps);
    28. //判空
    29. bool StackEmpty(ST* ps);

    Stack.c:

    1. #include"Stack.h"
    2. //初始化
    3. void StackInit(ST* ps)
    4. {
    5. 	assert(ps);
    6.  
    7. 	ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);
    8. 	if (ps->a == NULL)
    9. 	{
    10. 		printf("malloc fail!\n");
    11. 		exit(-1);
    12. 	}
    13.  
    14. 	ps->capacity = 4;
    15. 	ps->top = 0; //这使得top最终指向的是栈顶的后一个位置。若top=-1,则最终指向的是栈顶。
    16. }
    17. //释放内存、销毁空间
    18. void StackDestory(ST* ps)
    19. {
    20. 	assert(ps);
    21. 	free(ps->a);
    22. 	ps->a = NULL;
    23. 	ps->top = ps->capacity = 0;
    24. }
    25. // 入栈
    26. void StackPush(ST* ps, STDataType x)
    27. {
    28. 	assert(ps);
    29.  
    30. 	// 满了->增容
    31. 	if (ps->top == ps->capacity)
    32. 	{
    33. 		STDataType* tmp = (STDataType*)realloc(ps->a, ps->capacity * 2 * sizeof(STDataType));
    34. 		if (tmp == NULL)
    35. 		{
    36. 			printf("realloc fail!\n");
    37. 			exit(-1);
    38. 		}
    39. 		else
    40. 		{
    41. 			ps->a = tmp;
    42. 			ps->capacity *= 2;
    43. 		}
    44. 	}
    45.  
    46. 	ps->a[ps->top] = x;
    47. 	ps->top++;
    48. }
    49.  
    50. // 出栈
    51. void StackPop(ST* ps)
    52. {
    53. 	assert(ps);
    54. 	// 栈空了，再调用Pop，就会直接中止程序报错
    55. 	assert(ps->top > 0);
    56.  
    57. 	//ps->a[ps->top - 1] = 0; //置为0只考虑了int型等，若为char、double等就不适用了。
    58. 	ps->top--;
    59. }
    60. //取栈顶数据
    61. STDataType StackTop(ST* ps)
    62. {
    63. 	assert(ps);
    64. 	// 栈空了，再调用Top，就会直接中止程序报错
    65. 	assert(ps->top > 0);
    66.  
    67. 	return ps->a[ps->top - 1];
    68. }
    69. //求栈大小
    70. int StackSize(ST* ps)
    71. {
    72. 	assert(ps);
    73.  
    74. 	return ps->top;
    75. }
    76. //判空
    77. bool StackEmpty(ST* ps)
    78. {
    79. 	assert(ps);
    80. 	return ps->top == 0;
    81. }
    82.  
    83. //判断括号是否匹配算法
    84. bool isValid(char* s) {
    85. 	ST st;
    86. 	StackInit(&st);
    87. 	while (*s != '\0')
    88. 	{
    89. 		switch (*s)
    90. 		{
    91. 		case '{':
    92. 		case '[':
    93. 		case '(':
    94. 		{
    95. 			StackPush(&st, *s);
    96. 			++s;
    97. 			break;
    98. 		}
    99. 		case '}':
    100. 		case ']':
    101. 		case ')':
    102. 		{
    103. 			if (StackEmpty(&st))
    104. 			{
    105. 				StackDestory(&st);
    106. 				return false;
    107. 			}
    108.  
    109. 			char top = StackTop(&st);
    110. 			StackPop(&st);
    111.  
    112. 			// 不匹配
    113. 			if ((*s == '}' && top != '{')
    114. 				|| (*s == ']' && top != '[')
    115. 				|| (*s == ')' && top != '('))
    116. 			{
    117. 				StackDestory(&st);
    118. 				return false;
    119. 			}
    120. 			else // 匹配
    121. 			{
    122. 				++s;
    123. 			}
    124. 			break;
    125. 		}
    126. 		default:
    127. 			break;
    128. 		}
    129. 	}
    130. 	bool ret = StackEmpty(&st);
    131. 	StackDestory(&st);
    132. 	return ret;
    133. }

    3. 各大排序性能对比分析：

     1. 堆排序性能对比测试：

    测试代码：

    1. #pragma once
    2. #include
    3. #include
    4.  
    5. /
    6. //堆排序对比测试：
    7. void Swap(int* p1, int* p2)
    8. {
    9. 	int tmp = *p1;
    10. 	*p1 = *p2;
    11. 	*p2 = tmp;
    12. }
    13. //（1）建小堆，向上调整，最终为大堆---- - 用于堆排降序
    14. //1.堆排序调整-向下调整法
    15. void AdjustDwon1(int* a, int n, int root)
    16. {
    17. 	int parent = root;
    18. 	int child = parent * 2 + 1; // 默认是左孩子
    19. 	
    20. 	//建小堆，再调整
    21. 	while (child < n)
    22. 	{
    23. 		// 1、选出左右孩子中小的那一个
    24. 		if (child + 1 < n && a[child + 1] < a[child])
    25. 		{
    26. 			child += 1;
    27. 		}
    28.  
    29. 		if (a[child] < a[parent])
    30. 		{
    31. 			Swap(&a[child], &a[parent]);
    32. 			parent = child;
    33. 			child = parent * 2 + 1;
    34. 		}
    35. 		else
    36. 		{
    37. 			break;
    38. 		}
    39. 	}
    40. }
    41. //2.堆排序调整-向上调整法
    42. void AdjustUp1(int* a, int child)
    43. {
    44. 	int parent = (child - 1) / 2;
    45. 	//建小堆，再调整
    46. 	while (child > 0)
    47. 	{
    48. 		if (a[child] < a[parent])
    49. 		{
    50. 			Swap(&a[child], &a[parent]);
    51. 			child = parent;
    52. 			parent = (child - 1) / 2;
    53. 		}
    54. 		else
    55. 		{
    56. 			break;
    57. 		}
    58. 	}
    59. }
    60.  
    61. //堆排序（建堆）
    62. void HeapSort1(int* a, int n)
    63. {
    64. 	//建堆 调整
    65. 	//向上调整法
    66. 	for (int i = 1; i < n; ++i)
    67. 	{
    68. 		AdjustUp1(a, i);
    69. 	}
    70. 	
    71. 	int end = n - 1;
    72. 	while (end > 0)
    73. 	{
    74. 		Swap(&a[0], &a[end]);
    75. 		AdjustDwon1(a, end, 0);
    76. 		--end;
    77. 	}
    78. }
    79.  
    80. //（2）建大堆，向上调整，最终为小堆---- - 用于堆排升序
    81. //1.堆排序调整-向下调整法
    82. void AdjustDwon2(int* a, int n, int root)
    83. {
    84. 	int parent = root;
    85. 	int child = parent * 2 + 1; // 默认是左孩子
    86. 	//建大堆，再调整
    87. 	while (child < n)
    88. 	{
    89. 		// 1、选出左右孩子中大的那一个
    90. 		if (child + 1 < n && a[child + 1] > a[child])
    91. 		{
    92. 			child += 1;
    93. 		}
    94.  
    95. 		if (a[child] > a[parent])
    96. 		{
    97. 			Swap(&a[child], &a[parent]);
    98. 			parent = child;
    99. 			child = parent * 2 + 1;
    100. 		}
    101. 		else
    102. 		{
    103. 			break;
    104. 		}
    105. 	}
    106. }
    107. //2.堆排序调整-向上调整法
    108. void AdjustUp2(int* a, int child)
    109. {
    110. 	int parent = (child - 1) / 2;
    111. 	//1.建大堆，再调整
    112. 	while (child > 0)
    113. 	{
    114. 		if (a[child] > a[parent])
    115. 		{
    116. 			Swap(&a[child], &a[parent]);
    117. 			child = parent;
    118. 			parent = (child - 1) / 2;
    119. 		}
    120. 		else
    121. 		{
    122. 			break;
    123. 		}
    124. 	}
    125. }
    126.  
    127. //堆排序（建堆）
    128. void HeapSort2(int* a, int n)
    129. {
    130. 	// 建堆  调整
    131. 	//向上调整法
    132. 	for (int i = 1; i < n; ++i)
    133. 	{
    134. 		AdjustUp2(a, i);
    135. 	}
    136. 	
    137. 	int end = n - 1;
    138. 	while (end > 0)
    139. 	{
    140. 		Swap(&a[0], &a[end]);
    141. 		AdjustDwon2(a, end, 0);
    142. 		--end;
    143. 	}
    144. }
    145.  
    146. //（3）建小堆，向下调整，最终为大堆---- - 用于堆排降序（可以实现，多此一举）
    147. //1.堆排序调整-向下调整法
    148. void AdjustDwon3(int* a, int n, int root)
    149. {
    150. 	int parent = root;
    151. 	int child = parent * 2 + 1; // 默认是左孩子
    152. 	
    153. 	//建小堆，再调整
    154. 	while (child < n)
    155. 	{
    156. 		// 1、选出左右孩子中小的那一个
    157. 		if (child + 1 < n && a[child + 1] < a[child])
    158. 		{
    159. 			child += 1;
    160. 		}
    161.  
    162. 		if (a[child] < a[parent])
    163. 		{
    164. 			Swap(&a[child], &a[parent]);
    165. 			parent = child;
    166. 			child = parent * 2 + 1;
    167. 		}
    168. 		else
    169. 		{
    170. 			break;
    171. 		}
    172. 	}
    173. }
    174. //2.堆排序调整-向上调整法
    175. void AdjustUp3(int* a, int child)
    176. {
    177. 	int parent = (child - 1) / 2;
    178. 	
    179. 	//建小堆，再调整
    180. 	while (child > 0)
    181. 	{
    182. 		if (a[child] < a[parent])
    183. 		{
    184. 			Swap(&a[child], &a[parent]);
    185. 			child = parent;
    186. 			parent = (child - 1) / 2;
    187. 		}
    188. 		else
    189. 		{
    190. 			break;
    191. 		}
    192. 	}
    193. }
    194.  
    195. //堆排序（建堆）
    196. void HeapSort3(int* a, int n)
    197. {
    198. 	// 建堆 调整
    199. 	//向下调整法
    200. 	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
    201. 	{
    202. 		AdjustDwon3(a, n, i);
    203. 	}
    204. 	int end = n - 1;
    205. 	while (end > 0)
    206. 	{
    207. 		Swap(&a[0], &a[end]);
    208. 		AdjustDwon3(a, end, 0);
    209. 		--end;
    210. 	}
    211. }
    212.  
    213. //（4）建大堆，向下调整，最终为小堆---- - 用于堆排升序
    214. //1.堆排序调整-向下调整法
    215. void AdjustDwon4(int* a, int n, int root)
    216. {
    217. 	int parent = root;
    218. 	int child = parent * 2 + 1; // 默认是左孩子
    219. 	//建大堆，再调整
    220. 	while (child < n)
    221. 	{
    222. 		// 1、选出左右孩子中大的那一个
    223. 		if (child + 1 < n && a[child + 1] > a[child])
    224. 		{
    225. 			child += 1;
    226. 		}
    227.  
    228. 		if (a[child] > a[parent])
    229. 		{
    230. 			Swap(&a[child], &a[parent]);
    231. 			parent = child;
    232. 			child = parent * 2 + 1;
    233. 		}
    234. 		else
    235. 		{
    236. 			break;
    237. 		}
    238. 	}
    239. }
    240. //2.堆排序调整-向上调整法
    241. void AdjustUp4(int* a, int child)
    242. {
    243. 	int parent = (child - 1) / 2;
    244. 	//建大堆，再调整
    245. 	while (child > 0)
    246. 	{
    247. 		if (a[child] > a[parent])
    248. 		{
    249. 			Swap(&a[child], &a[parent]);
    250. 			child = parent;
    251. 			parent = (child - 1) / 2;
    252. 		}
    253. 		else
    254. 		{
    255. 			break;
    256. 		}
    257. 	}
    258. }
    259.  
    260. //堆排序（建堆）
    261. void HeapSort4(int* a, int n)
    262. {
    263. 	// 建堆 调整
    264. 	//向下调整法
    265. 	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
    266. 	{
    267. 		AdjustDwon4(a, n, i);
    268. 	}
    269. 	int end = n - 1;
    270. 	while (end > 0)
    271. 	{
    272. 		Swap(&a[0], &a[end]);
    273. 		AdjustDwon4(a, end, 0);
    274. 		--end;
    275. 	}
    276. }
    277.  
    278. void TestOP()
    279. {
    280. 	srand(time(0));
    281. 	const int N = 100000;
    282. 	int* a1 = (int*)malloc(sizeof(int) * N);
    283. 	int* a2 = (int*)malloc(sizeof(int) * N);
    284. 	int* a3 = (int*)malloc(sizeof(int) * N);
    285. 	int* a4 = (int*)malloc(sizeof(int) * N);
    286.  
    287. 	for (int i = 0; i < N; ++i)
    288. 	{
    289. 		a1[i] = rand();
    290. 		//a1[i] = i;
    291. 		a2[i] = a1[i];
    292. 		a3[i] = a1[i];
    293. 		a4[i] = a1[i];
    294.  
    295. 	}
    296.  
    297. 	int begin1 = clock();
    298. 	HeapSort1(a1, N);
    299. 	int end1 = clock();
    300.  
    301. 	int begin2 = clock();
    302. 	HeapSort2(a2, N);
    303. 	int end2 = clock();
    304.  
    305. 	int begin3 = clock();
    306. 	HeapSort3(a3, N);
    307. 	int end3 = clock();
    308.  
    309. 	int begin4 = clock();
    310. 	HeapSort4(a4, N);
    311. 	int end4 = clock();
    312.  
    313.  
    314. 	printf("建小堆-向上调整-降序:%d\n", end1 - begin1);
    315. 	printf("建大堆-向上调整-升序:%d\n", end2 - begin2);
    316. 	printf("建小堆-向下调整-降序:%d\n", end3 - begin3);
    317. 	printf("建大堆-向下调整-升序:%d\n", end4 - begin4);
    318.  
    319. 	free(a1);
    320. 	free(a2);
    321. 	free(a3);
    322. 	free(a4);
    323. }
    324.  
    325. int main()
    326. {
    327. 	TestOP();
    328. 	return 0;
    329. }

     2.快速排序（递归版）性能对比测试：

     3.各大排序测试对比代码：

    1. #pragma once
    2. #include
    3. #include
    4. #include
    5. #include"Stack.h"
    6. /
    7. //堆排序对比测试：
    8. void Swap(int* p1, int* p2)
    9. {
    10. 	int tmp = *p1;
    11. 	*p1 = *p2;
    12. 	*p2 = tmp;
    13. }
    14. //（1）建小堆，向上调整，最终为大堆---- - 用于堆排降序
    15. //1.堆排序调整-向下调整法
    16. void AdjustDwon1(int* a, int n, int root)
    17. {
    18. 	int parent = root;
    19. 	int child = parent * 2 + 1; // 默认是左孩子
    20. 	
    21. 	//建小堆，再调整
    22. 	while (child < n)
    23. 	{
    24. 		// 1、选出左右孩子中小的那一个
    25. 		if (child + 1 < n && a[child + 1] < a[child])
    26. 		{
    27. 			child += 1;
    28. 		}
    29.  
    30. 		if (a[child] < a[parent])
    31. 		{
    32. 			Swap(&a[child], &a[parent]);
    33. 			parent = child;
    34. 			child = parent * 2 + 1;
    35. 		}
    36. 		else
    37. 		{
    38. 			break;
    39. 		}
    40. 	}
    41. }
    42. //2.堆排序调整-向上调整法
    43. void AdjustUp1(int* a, int child)
    44. {
    45. 	int parent = (child - 1) / 2;
    46. 	//建小堆，再调整
    47. 	while (child > 0)
    48. 	{
    49. 		if (a[child] < a[parent])
    50. 		{
    51. 			Swap(&a[child], &a[parent]);
    52. 			child = parent;
    53. 			parent = (child - 1) / 2;
    54. 		}
    55. 		else
    56. 		{
    57. 			break;
    58. 		}
    59. 	}
    60. }
    61.  
    62. //堆排序（建堆）
    63. void HeapSort1(int* a, int n)
    64. {
    65. 	//建堆 调整
    66. 	//向上调整法
    67. 	for (int i = 1; i < n; ++i)
    68. 	{
    69. 		AdjustUp1(a, i);
    70. 	}
    71. 	
    72. 	int end = n - 1;
    73. 	while (end > 0)
    74. 	{
    75. 		Swap(&a[0], &a[end]);
    76. 		AdjustDwon1(a, end, 0);
    77. 		--end;
    78. 	}
    79. }
    80.  
    81. //（2）建大堆，向上调整，最终为小堆---- - 用于堆排升序
    82. //1.堆排序调整-向下调整法
    83. void AdjustDwon2(int* a, int n, int root)
    84. {
    85. 	int parent = root;
    86. 	int child = parent * 2 + 1; // 默认是左孩子
    87. 	//建大堆，再调整
    88. 	while (child < n)
    89. 	{
    90. 		// 1、选出左右孩子中大的那一个
    91. 		if (child + 1 < n && a[child + 1] > a[child])
    92. 		{
    93. 			child += 1;
    94. 		}
    95.  
    96. 		if (a[child] > a[parent])
    97. 		{
    98. 			Swap(&a[child], &a[parent]);
    99. 			parent = child;
    100. 			child = parent * 2 + 1;
    101. 		}
    102. 		else
    103. 		{
    104. 			break;
    105. 		}
    106. 	}
    107. }
    108. //2.堆排序调整-向上调整法
    109. void AdjustUp2(int* a, int child)
    110. {
    111. 	int parent = (child - 1) / 2;
    112. 	//1.建大堆，再调整
    113. 	while (child > 0)
    114. 	{
    115. 		if (a[child] > a[parent])
    116. 		{
    117. 			Swap(&a[child], &a[parent]);
    118. 			child = parent;
    119. 			parent = (child - 1) / 2;
    120. 		}
    121. 		else
    122. 		{
    123. 			break;
    124. 		}
    125. 	}
    126. }
    127.  
    128. //堆排序（建堆）
    129. void HeapSort2(int* a, int n)
    130. {
    131. 	// 建堆  调整
    132. 	//向上调整法
    133. 	for (int i = 1; i < n; ++i)
    134. 	{
    135. 		AdjustUp2(a, i);
    136. 	}
    137. 	
    138. 	int end = n - 1;
    139. 	while (end > 0)
    140. 	{
    141. 		Swap(&a[0], &a[end]);
    142. 		AdjustDwon2(a, end, 0);
    143. 		--end;
    144. 	}
    145. }
    146.  
    147. //（3）建小堆，向下调整，最终为大堆---- - 用于堆排降序（可以实现，多此一举）
    148. //1.堆排序调整-向下调整法
    149. void AdjustDwon3(int* a, int n, int root)
    150. {
    151. 	int parent = root;
    152. 	int child = parent * 2 + 1; // 默认是左孩子
    153. 	
    154. 	//建小堆，再调整
    155. 	while (child < n)
    156. 	{
    157. 		// 1、选出左右孩子中小的那一个
    158. 		if (child + 1 < n && a[child + 1] < a[child])
    159. 		{
    160. 			child += 1;
    161. 		}
    162.  
    163. 		if (a[child] < a[parent])
    164. 		{
    165. 			Swap(&a[child], &a[parent]);
    166. 			parent = child;
    167. 			child = parent * 2 + 1;
    168. 		}
    169. 		else
    170. 		{
    171. 			break;
    172. 		}
    173. 	}
    174. }
    175. //2.堆排序调整-向上调整法
    176. void AdjustUp3(int* a, int child)
    177. {
    178. 	int parent = (child - 1) / 2;
    179. 	
    180. 	//建小堆，再调整
    181. 	while (child > 0)
    182. 	{
    183. 		if (a[child] < a[parent])
    184. 		{
    185. 			Swap(&a[child], &a[parent]);
    186. 			child = parent;
    187. 			parent = (child - 1) / 2;
    188. 		}
    189. 		else
    190. 		{
    191. 			break;
    192. 		}
    193. 	}
    194. }
    195.  
    196. //堆排序（建堆）
    197. void HeapSort3(int* a, int n)
    198. {
    199. 	// 建堆 调整
    200. 	//向下调整法
    201. 	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
    202. 	{
    203. 		AdjustDwon3(a, n, i);
    204. 	}
    205. 	int end = n - 1;
    206. 	while (end > 0)
    207. 	{
    208. 		Swap(&a[0], &a[end]);
    209. 		AdjustDwon3(a, end, 0);
    210. 		--end;
    211. 	}
    212. }
    213.  
    214. //（4）建大堆，向下调整，最终为小堆---- - 用于堆排升序
    215. //1.堆排序调整-向下调整法
    216. void AdjustDwon4(int* a, int n, int root)
    217. {
    218. 	int parent = root;
    219. 	int child = parent * 2 + 1; // 默认是左孩子
    220. 	//建大堆，再调整
    221. 	while (child < n)
    222. 	{
    223. 		// 1、选出左右孩子中大的那一个
    224. 		if (child + 1 < n && a[child + 1] > a[child])
    225. 		{
    226. 			child += 1;
    227. 		}
    228.  
    229. 		if (a[child] > a[parent])
    230. 		{
    231. 			Swap(&a[child], &a[parent]);
    232. 			parent = child;
    233. 			child = parent * 2 + 1;
    234. 		}
    235. 		else
    236. 		{
    237. 			break;
    238. 		}
    239. 	}
    240. }
    241. //2.堆排序调整-向上调整法
    242. void AdjustUp4(int* a, int child)
    243. {
    244. 	int parent = (child - 1) / 2;
    245. 	//建大堆，再调整
    246. 	while (child > 0)
    247. 	{
    248. 		if (a[child] > a[parent])
    249. 		{
    250. 			Swap(&a[child], &a[parent]);
    251. 			child = parent;
    252. 			parent = (child - 1) / 2;
    253. 		}
    254. 		else
    255. 		{
    256. 			break;
    257. 		}
    258. 	}
    259. }
    260.  
    261. //堆排序（建堆）
    262. void HeapSort4(int* a, int n)
    263. {
    264. 	// 建堆 调整
    265. 	//向下调整法
    266. 	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
    267. 	{
    268. 		AdjustDwon4(a, n, i);
    269. 	}
    270. 	int end = n - 1;
    271. 	while (end > 0)
    272. 	{
    273. 		Swap(&a[0], &a[end]);
    274. 		AdjustDwon4(a, end, 0);
    275. 		--end;
    276. 	}
    277. }
    278.  
    279. //插入排序
    280. //时间复杂度：O(N^2)
    281. //最坏情况：逆序
    282. //最好情况：全部顺序 O(N)
    283. void InsertSort(int* a, int n)
    284. {
    285. 	//假设[0,end]有序，将end+1位置的值插入进去，让[0,end+1]有序
    286. 	for (int i = 0; i < n - 1; i++)
    287. 	{
    288. 		int end = i;
    289. 		int tmp = a[end + 1];
    290. 		while (end >= 0)
    291. 		{
    292. 			if (a[end] > tmp)  //升序
    293. 			//if (a[end] < tmp)  //降序
    294. 			{
    295. 				a[end + 1] = a[end];
    296. 				--end;
    297. 			}
    298. 			else
    299. 			{
    300. 				break;
    301. 			}
    302. 		}
    303. 		a[end + 1] = tmp;
    304. 	}
    305. }
    306. //快速排序——写法1：挖坑法(实现排序版)
    307. void QuickSort1(int* a, int left, int right)
    308. {
    309. 	if (left >= right)
    310. 		return;
    311. 	int begin = left, end = right;
    312. 	int pivot = begin;
    313. 	int key = a[begin];  //指定了第一次关键字为begin
    314.  
    315. 	while (begin < end)   //单趟排序
    316. 	{
    317. 		//右边找小，放到左边
    318. 		while (begin < end && a[end] >= key)
    319. 		{
    320. 			--end;
    321. 		}
    322. 		//小的放到左边的坑里，自己形成新的坑位
    323. 		a[pivot] = a[end];
    324. 		pivot = end;
    325. 		//左边找大
    326. 		while (begin < end && a[begin] <= key)
    327. 		{
    328. 			++begin;
    329. 		}
    330. 		//大的放到左边的坑里，自己形成新的坑位
    331. 		a[pivot] = a[begin];
    332. 		pivot = begin;
    333.  
    334. 	}
    335. 	pivot = begin;
    336. 	a[pivot] = key;
    337.  
    338. 	// [left, right]
    339. 	// [left, pivot-1] pivot [pivot+1, right]	
    340. 	// 左子区间和右子区间有序，我们就有序了，如果让他们有序呢？ 分治递归
    341. 	QuickSort1(a, left, pivot - 1);
    342. 	QuickSort1(a, pivot + 1, right);
    343. }
    344.  
    345.  
    346. //快速排序——写法2：挖坑法优化--->（三数取中，解决原始数据有序情况）,再根据处理量分情况排序（小区间优化）
    347. // 三数取中
    348. int GetMidIndex(int* a, int left, int right)
    349. {
    350. 	int mid = (left + right) >> 1;
    351. 	if (a[left] < a[mid])
    352. 	{
    353. 		if (a[mid] < a[right])
    354. 		{
    355. 			return mid;
    356. 		}
    357. 		else if (a[left] > a[right])
    358. 		{
    359. 			return left;
    360. 		}
    361. 		else
    362. 		{
    363. 			return right;
    364. 		}
    365. 	}
    366. 	else // a[left] > a[mid]
    367. 	{
    368. 		if (a[mid] > a[right])
    369. 		{
    370. 			return mid;
    371. 		}
    372. 		else if (a[left] < a[right])
    373. 		{
    374. 			return left;
    375. 		}
    376. 		else
    377. 		{
    378. 			return right;
    379. 		}
    380. 	}
    381. }
    382. void QuickSort2(int* a, int left, int right)
    383. {
    384. 	if (left >= right)
    385. 		return;
    386. 	int keyIndex = GetMidIndex(a, left, right);
    387. 	Swap(&a[left], &a[keyIndex]);
    388.  
    389. 	int begin = left, end = right;
    390. 	int pivot = begin;
    391. 	int key = a[begin];
    392.  
    393. 	// O（N）
    394. 	while (begin < end)
    395. 	{
    396. 		// 右边找小，放到左边
    397. 		while (begin < end && a[end] >= key)
    398. 			--end;
    399.  
    400. 		// 小的放到左边的坑里，自己形成新的坑位
    401. 		a[pivot] = a[end];
    402. 		pivot = end;
    403.  
    404. 		// 左边找大
    405. 		while (begin < end && a[begin] <= key)
    406. 			++begin;
    407.  
    408. 		// 大的放到左边的坑里，自己形成新的坑位
    409. 		a[pivot] = a[begin];
    410. 		pivot = begin;
    411. 	}
    412.  
    413. 	pivot = begin;
    414. 	a[pivot] = key;
    415.  
    416. 	// 小区间优化
    417. 	//这个值会随原始数据量改变，而官方给13左右
    418. 	if (pivot - 1 - left > 10)   //官方给13左右
    419. 	{
    420. 		QuickSort2(a, left, pivot - 1);
    421. 	}
    422. 	else
    423. 	{
    424. 		//InsertSort(int* a, int n)
    425. 		InsertSort(a + left, pivot - 1 - left + 1);  //left不一定从0开始，传数据个数
    426. 	}
    427.  
    428. 	if (right - (pivot + 1) > 10)
    429. 	{
    430. 		QuickSort2(a, pivot + 1, right);
    431. 	}
    432. 	else
    433. 	{
    434. 		InsertSort(a + pivot + 1, right - (pivot + 1) + 1);
    435. 	}
    436. }
    437.  
    438. //快速排序——写法3：左右指针法：找小找大交换
    439. void QuickSort3(int* a, int left, int right)
    440. {
    441. 	if (left >= right)
    442. 		return;
    443.  
    444. 	int index = GetMidIndex(a, left, right);
    445. 	Swap(&a[left], &a[index]);
    446.  
    447. 	int begin = left, end = right;
    448. 	int keyi = begin;
    449.  
    450. 	while (begin < end)
    451. 	{
    452. 		// 找小
    453. 		while (begin < end && a[end] >= a[keyi])
    454. 		{
    455. 			--end;
    456. 		}
    457.  
    458. 		// 找大
    459. 		while (begin < end && a[begin] <= a[keyi])
    460. 		{
    461. 			++begin;
    462. 		}
    463.  
    464. 		Swap(&a[begin], &a[end]);
    465. 	}
    466.  
    467. 	Swap(&a[begin], &a[keyi]);
    468. 	int key = begin;
    469.  
    470. 	// 小区间优化
    471. 	//这个值会随原始数据量改变，而官方给13左右
    472. 	if (key - 1 - left > 10)   //官方给13左右
    473. 	{
    474. 		QuickSort3(a, left, key - 1);
    475. 	}
    476. 	else
    477. 	{
    478. 		//InsertSort(int* a, int n)
    479. 		InsertSort(a + left, key - 1 - left + 1);  //left不一定从0开始，传数据个数
    480. 	}
    481.  
    482. 	if (right - (key + 1) > 10)
    483. 	{
    484. 		QuickSort3(a, key + 1, right);
    485. 	}
    486. 	else
    487. 	{
    488. 		InsertSort(a + key + 1, right - (key + 1) + 1);
    489. 	}
    490. }
    491.  
    492. //快速排序——写法4：前后指针法：cur找小，每次找到比keyi小额值，就++prev，然后交换prev与cur的位置交换
    493. //1.会有自己与自己交换的情况，2.也有异步交换，3.最后实现左边全为小于key,右边全为大于key
    494.  
    495. void QuickSort4(int* a, int left, int right)
    496. {
    497. 	if (left >= right)
    498. 		return;
    499.  
    500. 	int index = GetMidIndex(a, left, right);
    501. 	Swap(&a[left], &a[index]);
    502.  
    503. 	int keyi = left;
    504. 	int prev = left, cur = left + 1;
    505. 	while (cur <= right)
    506. 	{
    507. 		if (a[cur] < a[keyi]
    508. 			&& ++prev != cur)   //++prev != cur：优化自己与自己交换的情况
    509. 		{
    510. 			Swap(&a[prev], &a[cur]);
    511. 		}
    512.  
    513. 		++cur;
    514. 	}
    515.  
    516. 	Swap(&a[keyi], &a[prev]);
    517.  
    518. 	int key = prev;
    519. 	// 小区间优化
    520. 	//这个值会随原始数据量改变，而官方给13左右
    521. 	if (key - 1 - left > 10)   //官方给13左右
    522. 	{
    523. 		QuickSort4(a, left, key - 1);
    524. 	}
    525. 	else
    526. 	{
    527. 		//InsertSort(int* a, int n)
    528. 		InsertSort(a + left, key - 1 - left + 1);  //left不一定从0开始，传数据个数
    529. 	}
    530.  
    531. 	if (right - (key + 1) > 10)
    532. 	{
    533. 		QuickSort4(a, key + 1, right);
    534. 	}
    535. 	else
    536. 	{
    537. 		InsertSort(a + key + 1, right - (key + 1) + 1);
    538. 	}
    539. }
    540. //快速排序——非递归版
    541. //（复杂一点）使用数据结构的栈进行模拟递归过程：不会再有栈溢出问题，也会有空间消耗
    542. //但数据结构中的栈是malloc出来的，开辟在堆（操作系统对内存的划分），而堆的空间比栈大
    543. void QuickSortNonR(int* a, int n)
    544. {
    545. 	ST st;
    546. 	StackInit(&st);
    547. 	StackPush(&st, n - 1);
    548. 	StackPush(&st, 0);
    549. 	while (!StackEmpty(&st))
    550. 	{
    551. 		int left = StackTop(&st);
    552. 		StackPop(&st);
    553. 		int right = StackTop(&st);
    554. 		StackPop(&st);
    555. 		//调用单趟排序
    556. 		int index = GetMidIndex(a, left, right);
    557. 		//Swap(&a[left], &a[index]);
    558.  
    559. 		int keyi = left;
    560. 		int prev = left, cur = left + 1;
    561. 		while (cur <= right)
    562. 		{
    563. 			if (a[cur] < a[keyi]
    564. 				&& ++prev != cur)   //++prev != cur：优化自己与自己交换的情况
    565. 			{
    566. 				Swap(&a[prev], &a[cur]);
    567. 			}
    568.  
    569. 			++cur;
    570. 		}
    571.  
    572. 		Swap(&a[keyi], &a[prev]);
    573. 		int keyIndex = prev;
    574.  
    575. 		//栈里面的就需要单趟分割排序
    576. 		//[left,keyIndex-1] keyIndex [keyIndex+1,right]
    577. 		if (keyIndex + 1 < right)
    578. 		{
    579. 			StackPush(&st, right);
    580. 			StackPush(&st, keyIndex + 1);
    581.  
    582. 		}
    583. 		if (left < keyIndex - 1)
    584. 		{
    585. 			StackPush(&st, keyIndex - 1);
    586. 			StackPush(&st, left);
    587. 		}
    588. 	}
    589. 	StackDestory(&st);
    590.  
    591. }
    592. void ShellSort(int* a, int n)
    593. {
    594. 	int gap = n;  //可以自行设置，但不会给固定的值
    595. 	//把间隔为gap的多组数据同时排序（注意：理解这个多组的含义）
    596. 	//end最终位置：n-gap-1
    597. 	//gap的设置方式之一：
    598. 	while (gap > 1)
    599. 	{
    600. 		//gap=gap/2;        //一定会保证最后一次为1    //运行了logN次
    601. 		gap = gap / 3 + 1;  //但要保证最后一次为1      //运行了log3N次
    602. 		//gap>1时都是预排序，排序后接近有序
    603. 		//gap==1时，就是直接插入排序
    604.  
    605. 		for (int i = 0; i < n - gap; i++)
    606. 		{
    607. 			int end = i;
    608. 			int tmp = a[end + gap];
    609. 			while (end >= 0)
    610. 			{
    611. 				if (a[end] > tmp)
    612. 				{
    613. 					a[end + gap] = a[end];
    614. 					end -= gap;
    615. 				}
    616. 				else
    617. 				{
    618. 					break;
    619. 				}
    620. 			}
    621. 			a[end + gap] = tmp;
    622. 		}
    623. 	}
    624.  
    625. }
    626. void BubbleSort(int* a, int n)
    627. {
    628. 	//写法1：
    629. 	for (int j = 0; j < n; ++j)
    630. 	{
    631. 		int exchange = 0;
    632. 		for (int i = 1; i < n - j; ++i)
    633. 		{
    634. 			if (a[i - 1] > a[i])
    635. 			{
    636. 				Swap(&a[i - 1], &a[i]);
    637. 				exchange = 1;
    638. 			}
    639. 		}
    640.  
    641. 		if (exchange == 0)
    642. 		{
    643. 			break;
    644. 		}
    645. 	}
    646. 	写法2：
    647. 	//int end = n;
    648. 	//while (end > 0)
    649. 	//{
    650. 	//	for (int i = 1; i < end; ++i)
    651. 	//	{
    652. 	//		if (a[i - 1] > a[i])
    653. 	//		{
    654. 	//			Swap(&a[i - 1], &a[i]);
    655. 	//		}
    656. 	//	}
    657. 	//	--end;
    658. 	//}
    659. }
    660. void _MergeSort(int* a, int left, int right, int* tmp)
    661. {
    662. 	if (left >= right)
    663. 		return;
    664.  
    665. 	int mid = (left + right) >> 1;
    666. 	//假设 [left, mid] [mid+1, right]有序，那么我们就可以归并了
    667. 	_MergeSort(a, left, mid, tmp);
    668. 	_MergeSort(a, mid + 1, right, tmp);
    669.  
    670. 	// 归并
    671. 	int begin1 = left, end1 = mid;
    672. 	int begin2 = mid + 1, end2 = right;
    673. 	int index = left;
    674. 	while (begin1 <= end1 && begin2 <= end2)
    675. 	{
    676. 		if (a[begin1] < a[begin2])
    677. 		{
    678. 			tmp[index++] = a[begin1++];
    679. 		}
    680. 		else
    681. 		{
    682. 			tmp[index++] = a[begin2++];
    683. 		}
    684. 	}
    685.  
    686. 	while (begin1 <= end1)
    687. 	{
    688. 		tmp[index++] = a[begin1++];
    689. 	}
    690.  
    691. 	while (begin2 <= end2)
    692. 	{
    693. 		tmp[index++] = a[begin2++];
    694. 	}
    695.  
    696. 	// 拷贝回去
    697. 	for (int i = left; i <= right; ++i)
    698. 	{
    699. 		a[i] = tmp[i];
    700. 	}
    701. }
    702.  
    703. void MergeSort(int* a, int n)
    704. {
    705. 	int* tmp = (int*)malloc(sizeof(int) * n); //空间复杂度为O(N)
    706. 	_MergeSort(a, 0, n - 1, tmp);
    707. 	free(tmp);
    708. }
    709. void MergeSortNonR(int* a, int n)
    710. {
    711. 	int* tmp = (int*)malloc(sizeof(int) * n);
    712. 	int gap = 1;  //每组数据个数
    713. 	while (gap < n)
    714. 	{
    715. 		for (int i = 0; i < n; i += 2 * gap)
    716. 		{
    717. 			//[i,i+gap-1] [i+gap,i+2*gap-1]
    718.  
    719. 			// 归并
    720. 			int begin1 = i, end1 = i + gap - 1;
    721. 			int begin2 = i + gap, end2 = i + 2 * gap - 1;
    722. 			//归并过程中右半区间可能就不存在
    723. 			if (begin2 >= n)
    724. 				break;
    725. 			//归并过程中右半区间算多了,修正
    726. 			if (end2 >= n)
    727. 			{
    728. 				end2 = n - 1;
    729. 			}
    730. 			int index = i;
    731. 			while (begin1 <= end1 && begin2 <= end2)
    732. 			{
    733. 				if (a[begin1] < a[begin2])
    734. 				{
    735. 					tmp[index++] = a[begin1++];
    736. 				}
    737. 				else
    738. 				{
    739. 					tmp[index++] = a[begin2++];
    740. 				}
    741. 			}
    742.  
    743. 			while (begin1 <= end1)
    744. 			{
    745. 				tmp[index++] = a[begin1++];
    746. 			}
    747.  
    748. 			while (begin2 <= end2)
    749. 			{
    750. 				tmp[index++] = a[begin2++];
    751. 			}
    752. 			// 拷贝回去
    753. 			for (int j = i; j < end2; ++j)
    754. 			{
    755. 				a[j] = tmp[j];
    756. 			}
    757. 		}
    758. 		gap *= 2;
    759. 	}
    760. 	free(tmp);
    761. }
    762. void CountSort(int* a, int n)
    763. {
    764. 	int min = a[0], max = a[0];
    765. 	for (int i = 1; i < n; ++i)
    766. 	{
    767. 		if (a[i] < min)
    768. 			min = a[i];
    769. 		if (a[i] > max)
    770. 			max = a[i];
    771. 	}
    772.  
    773. 	int range = max - min + 1;
    774. 	int* countA = (int*)malloc(sizeof(int) * range);
    775. 	assert(countA);
    776.  
    777. 	memset(countA, 0, sizeof(int) * range);
    778. 	//计数
    779. 	for (int i = 0; i < n; ++i)
    780. 		countA[a[i] - min]++;
    781. 	//排序
    782. 	int j = 0;
    783. 	for (int i = 0; i < range; ++i)
    784. 	{
    785. 		while (countA[i]--)
    786. 		{
    787. 			a[j++] = i + min;
    788. 		}
    789. 	}
    790. }
    791.  
    792. void TestOP()
    793. {
    794. 	srand(time(0));
    795. 	const int N = 1000000;
    796. 	int* a1 = (int*)malloc(sizeof(int) * N);
    797. 	int* a2 = (int*)malloc(sizeof(int) * N);
    798. 	int* a3 = (int*)malloc(sizeof(int) * N);
    799. 	int* a4 = (int*)malloc(sizeof(int) * N);
    800. 	int* a5 = (int*)malloc(sizeof(int) * N);
    801. 	int* a6 = (int*)malloc(sizeof(int) * N);
    802. 	int* a7 = (int*)malloc(sizeof(int) * N);
    803. 	int* a8 = (int*)malloc(sizeof(int) * N);
    804. 	int* a9 = (int*)malloc(sizeof(int) * N);
    805. 	int* a10 = (int*)malloc(sizeof(int) * N);
    806. 	int* a11 = (int*)malloc(sizeof(int) * N);
    807. 	int* a12 = (int*)malloc(sizeof(int) * N);
    808. 	int* a13 = (int*)malloc(sizeof(int) * N);
    809. 	int* a14 = (int*)malloc(sizeof(int) * N);
    810.  
    811. 	for (int i = 0; i < N; ++i)
    812. 	{
    813. 		a1[i] = rand();
    814. 		//a1[i] = i;
    815. 		a2[i] = a1[i];
    816. 		a3[i] = a1[i];
    817. 		a4[i] = a1[i];
    818. 		a5[i] = a1[i];
    819. 		a6[i] = a1[i];
    820. 		a7[i] = a1[i];
    821. 		a8[i] = a1[i];
    822. 		a9[i] = a1[i];
    823. 		a10[i] = a1[i];
    824. 		a11[i] = a1[i];
    825. 		a12[i] = a1[i];
    826. 		a13[i] = a1[i];
    827. 		a14[i] = a1[i];
    828.  
    829. 	}
    830.  
    831. 	int begin1 = clock();
    832. 	//HeapSort1(a1, N);
    833. 	int end1 = clock();
    834.  
    835. 	int begin2 = clock();
    836. 	//HeapSort2(a2, N);
    837. 	int end2 = clock();
    838.  
    839. 	int begin3 = clock();
    840. 	//HeapSort3(a3, N);
    841. 	int end3 = clock();
    842.  
    843. 	int begin4 = clock();
    844. 	//HeapSort4(a4, N);
    845. 	int end4 = clock();
    846.  
    847. 	int begin5 = clock();
    848. 	QuickSort1(a5, 0, N - 1);
    849. 	int end5 = clock();
    850.  
    851. 	int begin6 = clock();
    852. 	QuickSort2(a6, 0, N - 1);
    853. 	int end6 = clock();
    854.  
    855. 	int begin7 = clock();
    856. 	QuickSort3(a7, 0, N - 1);
    857. 	int end7 = clock();
    858.  
    859. 	int begin8 = clock();
    860. 	QuickSort4(a8, 0, N - 1);
    861. 	int end8 = clock();
    862.  
    863. 	int begin9 = clock();
    864. 	QuickSortNonR(a9, N);
    865. 	int end9 = clock();
    866.  
    867. 	int begin10 = clock();
    868. 	//ShellSort(a10, N);
    869. 	int end10 = clock();	
    870.  
    871. 	int begin11 = clock();
    872. 	//BubbleSort(a11, N);
    873. 	int end11 = clock();	
    874.  
    875. 	int begin12 = clock();
    876. 	//MergeSort(a12, N);
    877. 	int end12 = clock();	
    878.  
    879. 	int begin13= clock();
    880. 	//MergeSortNonR(a13, N);
    881. 	int end13 = clock();	
    882.  
    883. 	int begin14 = clock();
    884. 	//CountSort(a14, N);
    885. 	int end14 = clock();
    886.  
    887. 	printf("给定%d个随机数进行排序，测试对比各大排序性能（单位：ms):\n", N);
    888. 	printf("建小堆-向上调整-降序:\t%d\n", end1 - begin1);
    889. 	printf("建大堆-向上调整-升序:\t%d\n", end2 - begin2);
    890. 	printf("建小堆-向下调整-降序:\t%d\n", end3 - begin3);
    891. 	printf("建大堆-向下调整-升序:\t%d\n", end4 - begin4);
    892. 	printf("快速排序-挖坑法:    \t%d\n", end5 - begin5);
    893. 	printf("快速排序-挖坑法优化:\t%d\n", end6 - begin6);
    894. 	printf("快速排序-左右指针法:\t%d\n", end7 - begin7);
    895. 	printf("快速排序-前后指针法:\t%d\n", end8 - begin8);
    896. 	printf("快速排序-非递归:    \t%d\n", end9 - begin9);
    897. 	printf("希尔排序:          \t%d\n", end10 - begin10);
    898. 	printf("冒泡排序:          \t%d\n", end11 - begin11);
    899. 	printf("归并排序:          \t%d\n", end12 - begin12);
    900. 	printf("归并排序-非递归:    \t%d\n", end13 - begin13);
    901. 	printf("计数排序:          \t%d\n", end14 - begin14);
    902.  
    903.  
    904.  
    905. 	free(a1);
    906. 	free(a2);
    907. 	free(a3);
    908. 	free(a4);
    909. 	free(a5);
    910. 	free(a6);
    911. 	free(a7);
    912. 	free(a8);
    913. 	free(a9);
    914. 	free(a10);
    915. 	free(a11);
    916. 	free(a12);
    917. 	free(a13);
    918. 	free(a14);
    919. }
    920.  
    921. int main()
    922. {
    923. 	TestOP();
    924. 	return 0;
    925. }

    后记：
    ●由于作者水平有限，文章难免存在谬误之处，敬请读者斧正，俚语成篇，恳望指教！

                                                                               ——By 作者：新晓·故知

  • 相关阅读:
    SQL 和 NoSQL 有什么区别？
    混合IT基础设施的安全挑战与缓解策略
    电脑重装系统后usbcleaner怎么格式化u盘
    Linux 装机必备
    隐马尔科夫模型（HMM）学习笔记
    【WSN通信】基于最佳簇半径的无线传感器网络分簇路由算法附matlab代码
    “咕”了 73 天，何同学终于回归：最喜欢 3D 打印机，但不要买
    NumPy中einsum使用笔记
    后端老项目迁移方法
    利用datafaker批量生成测试数据
  • 原文地址：https://blog.csdn.net/m0_57859086/article/details/126631517