-
【推荐系统】推荐基础算法-基于稀疏自编码的推荐方法
矩阵分解技术在推荐领域的应用比较成熟,矩阵分解本质上只通过一次分解来对原矩阵进行逼近,特征挖掘的层次不够深入。另外矩阵分解也没有运用到物品本身的内容特征,例如书本的类别分类、音乐的流派分类等。通过多层感知机,可以得到更加深度的特征表示,并且可以对内容分类特征加以应用。
1.基础的自编码结构
假设我们有一个训练样本集合{x(1),x(2),x(3)...},其 ,即每一个样本均有n维特征。构造一个三层的神经网络,输入层layer1是
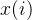 ,输入层layer3是
,输入层layer3是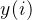 ,中间隐藏层layerl2为
,中间隐藏层layerl2为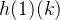 ,我们让输出层等于输入层,
,我们让输出层等于输入层,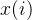 =
= 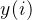 ,且中间层的维度远远低于输入层和输出层,这样就得到了第一层的特征压缩
,且中间层的维度远远低于输入层和输出层,这样就得到了第一层的特征压缩 自编码神经网络尝试逼近一个恒等函数,从而使得输出x'接近于输入x。当我们为自编码神经网络加入某些限制,比如限定隐藏神经元的数量,我们就可以从输入数据中发现一些有趣的结构。
假设某个自编码神经网络的输入x是100维的数据,其隐藏层L2我们限定为50个隐藏神经元,输出也是100维的y由于只有50个隐藏神经元,我们迫使自编码神经网络去学习输入数据的压缩表示,也就是说,它必须从50维的隐藏神经元的激活项中重构出100维的输入。如果网络的输入数据是完全随机的,比如每一个输入都是一个跟其他特征完全无关的独立同分布高斯随机变量,那么这一压缩表示将会非常难于学习。但是如果输入数据中隐含着一些特定的结构,比如某些输入特征是彼此相关的,那么这一算法就可以发现输入数据中的这些相关性。
当隐藏神经元的数量较大(有时为了能更有效地找出隐含在输入数据内部的结构与模式,会寻找一组超完备基向量,其维度可能比输入的维度还要高),也可以通过给自编码神经网络施加一些限制,使得满足稀疏性要求;如果神经元的输出接近于1的时候我们认为它被激活,而输出接近于0的时候认为它被抑制,即我们通常说的dropout。那么使得神经元大部分的时间都是被抑制的限制则被称作稀疏性限制。
2.多层结构
- 用深度学习的一些思想,学习到高层抽象特征,其中一种典型的方法就是栈式自编码,它采用逐层贪婪训练法进行训练。即先利用原始输入来训练第一个网络,通过使输出接近于输入,我们可以得到第一个网络的隐藏层h(1)(k)。
- 我们用原始输入(x)训练第一个自编码器,它能够学习得到原始输入的一阶特征表示隐藏层h(1)(k),再将这些一阶特征作为第二个稀疏自编码器的输入,来学习二阶特征h(2)(k)
- 再将二阶特征h(2)(k)作为第三个网络,一个softmax分类器的输入,训练出一个能将二阶特征映射到数字标签的模型
- 将这三层网络结合起来构建一个包含原始输入层,两个隐藏层和一个最终softmax分类器层的完整的栈式自编码网络
我们以音乐推荐为例,输入层的每个样本是一首歌曲,向量特征为歌曲被用户收藏的数据,输出层为音乐的流派分类结果。我们希望训练出歌曲的特征向量,用于歌曲相似度的计算,具体构造自编码网络的方法如下:
输入层,每首歌曲的输入向量为(u1,u2,u3,……,u],其中ui表示用户i是否收藏过这首歌,当收藏过时,值为1;未收藏时,值是缺失的,暂且计为0。输入矩阵为(m+1)xn维(包含一个截距项),m为用户数量,n为歌曲数量。
隐藏层1、隐藏层2,强制指定神经元的数量为k+1个,此时隐藏层其实就是歌曲的低维特征向量,矩阵为(k+1)xn,k+1为特征维数(包含一个截距项1,之所以保留,是为了可以重构出输出层),其中n为歌曲数量。
一般的神经网络中,往往会忽略隐藏层到输出层的连接权重W(1,1)、W(1,2)、b(1,1)、b(1,2)的意义,只是将其作为一个输出预测的分类器;但在自编码网络中,连接层是有实际意义的,这些权重作用是将歌曲特征向量映射到用户是否听过/喜欢过该歌曲,其实就是用户的低维特征
输出层是音乐流派的分类结果
通过展示栈式自编码的学习,可以将隐藏层h(2)(k)取出来,它是歌曲以流派分类为目标降维压缩后的向量,该向量不仅使用到了用户的群体收藏行为还用到了歌曲的流派特征信息,可以表示歌曲更多的特征信息。类似SVD,我们可以通过歌曲的特征向量求得歌曲的相似度,对用户未收藏的歌曲进行打分
-
相关阅读:
Android中简单实现Spinner的数据绑定
智慧停车视频解决方案:如何让AI助力停车管理升级?
瑞_Redis_短信登录(二)
Learn Prompt-ChatGPT 精选案例:学习各国语言
深入浅出WMS之入库流程解析
【Linux】常用命令
利用emotion数据集微调deberta-v3-large大模型的文本分类
CleanMyMac苹果电脑清理软件是智商税吗?最全评测价格、清理效果一次说清
如何在Linux上搭建本地Docker Registry并实现远程连接
Java观察者模式之总有你想不到的知识
- 原文地址:https://blog.csdn.net/m0_51933492/article/details/126665265