双连通与网络可靠性

1. 割点的定义

如果去掉有向图G中的顶点v及其关联的边，剩下的图将不再联通，则顶点v被称为割点。

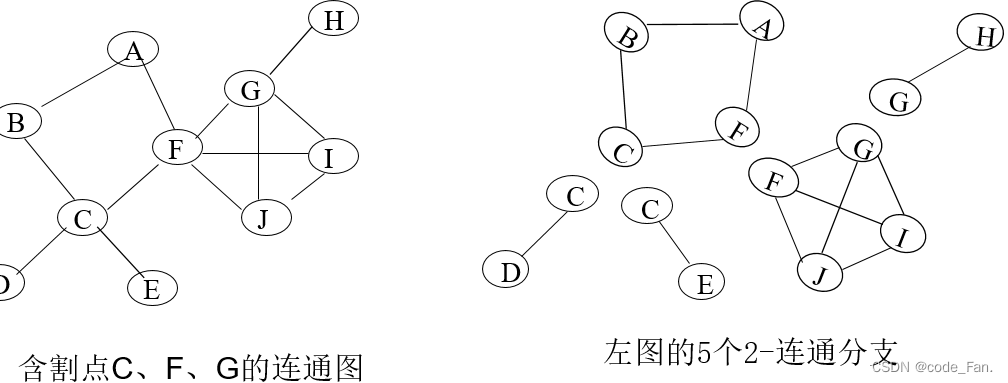
2. 双连通的定义

没有割点的连通图称为2-连通的（也称为块）。图G中极大的2-连通子图称为G的一个2-连通分支。

3. 深索数的定义

当采用深度优先遍历算法时，顶点v被访问的序数称为v的深索数，记做DFN(v)

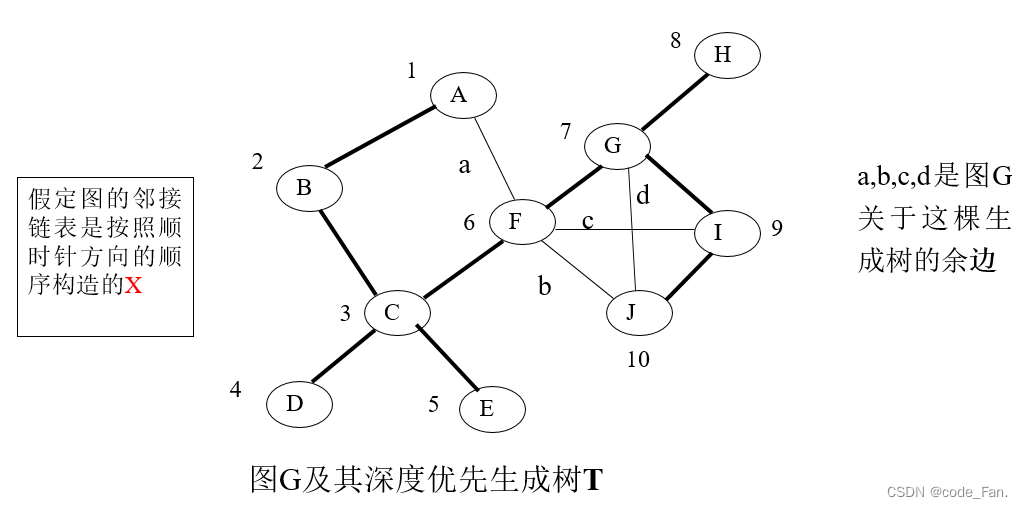
4. 割点的特征分析

(1) 关于深度优先搜索树T，图G的每一条边（u，v）的两个端点u、v之间，或u是v的祖先，或v是u的祖先，即不是平辈关系。
(2) 树T的根是图G的割点当且仅当其在T中至少有两个子节点。
(3) 如果节点u既不是根也不是叶，那么它不是G的割点当且仅当u在深度优先搜索树T中的每个子节点w都至少有一个子孙（或w本身）关联着一条边e（实际上是余边），e的另一个端点是u的某个祖先（e一定是树T的余边）。
(4) 叶节点不能是割点。
由（3）、（4）可知，深度优先搜索树T的非根节点u是G的割点当且仅当u至少有一个儿子w，w及其子孙都不与u的任何祖先相邻。同时u的深索数一定小于其子孙的深索数，所以深索数DFN并不能反映一个顶点是否是割点的情况。为此，我们递归地定义各个顶点u的最低深索数L(u)

5. 最低深索数L(u)

顶点u的最低深索数L(u)定义为

L(u) = min{DFN(u), min{DFN(x)|(u,x)是T的余边},min{L(w)|w是u的子节点}}
1

结论：如果u不是深度优先搜索树的根，则u是图G的割点当且仅当u有某个子节点w看，w的最低深索数不小于u的深索数，即存在v的子节点w，使得

L(w)>=DFN(u)
1