codeforces：E. Madoka and The Best University【因数list + 分析拆解 + 公因数特性 + 欧拉函数】

分析

显然先固定c，那么ab之和固定设为sum
gcd(a,b) = gcd(a, sum) = factor 【这个factor是sum的因数，我们先要来一个list存每个数的因数的】
特别地，化简以下，gcd(a // factor, sum // factor) = 1
我们要看有多少个这样的a满足gcd(a // factor, sum // factor) = 1
这里就要用到欧拉函数：

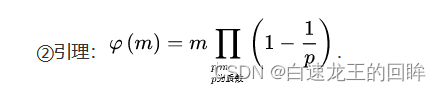
把sum // factor的质因数都找出来，套入公式即可
这样sigma求和就变成一个具体的数了
也就是说当c固定，gcd(a, b)固定时，我们找出有多少组即可

某马ac code

import sys

input = sys.stdin.readline
import functools
import math




def lcm(a, b):
    return int(a * b / math.gcd(a, b))


for _ in range(1):

    n = int(input())

    ## 从因子入手，获取每个数的因数
    factor = [] * n
    for i in range(n + 1):
        factor.append([])
    for i in range(1, n + 1):
        k = 1
        while k * i <= n:
            factor[k * i].append(i)
            k += 1

    ## pairs[i]和为i的两个数a, b
    ## 有多少个a和i互质
    ## 用到欧拉函数
    pairs = [0] * n
    pairs[2] = 1
    for i in range(3, n):
        nums = i
        for small in factor[i]:
            # 保证zhishu
            if len(factor[small]) == 2:
                nums *= (small - 1) / small
        pairs[i] = int(nums)


    ans = 0
    for i in range(1, n - 1):
        # 固定c为i，ab之和为sum
        sums = n - i
        # gcd(a, b) = gcd(a, sum)
        # 遍历sum的因子
        for factors in factor[sums]:
            if factors != sums:
                # 因子为factors的话
                # gcd(a, sum) = factors => gcd(a // factors, sum // factors) = 1
                # 那么这样的a的个数就是pairs[sums // factors]
                ans += lcm(i, factors) * pairs[sums // factors]

        ans %= 1000000007

    # 特判
    if n == 3:
        ans = 1
    print(ans)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

总结

拆分问题，将变量转为ab
然后ab和固定的话，gcd(a, b) = gcd(a, sum) = one factor of sum
有多少组呢？
gcd(a // factor, sum // factor) = 1 使用欧拉函数即可
可以求出跟sum // factor互质的数的个数（公式就是去重的意思）