数据结构与算法之美读书笔记15

二分查找的变形问题

（以数据是从小到大排列为前提）

1.查找第一个值等于给定值的元素

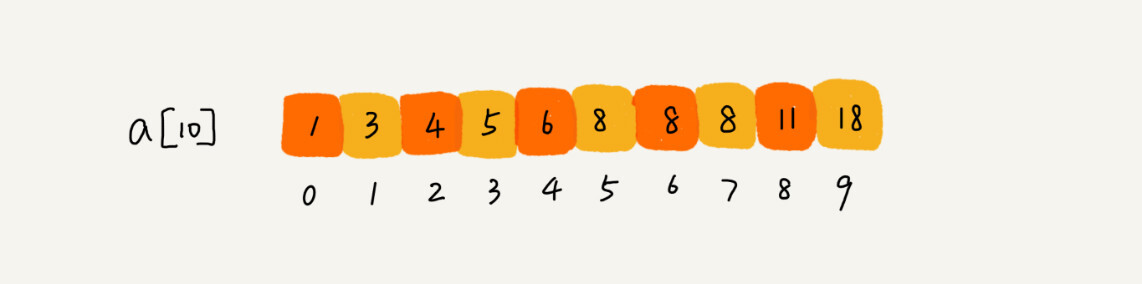
首先拿8与区间的中间值a[4]比较，8比6大，于是在下标5到9之间继续查找。下标5和9的中间位置是下标7，a[7]正好等于8，所以代码就返回了。

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == 0) || (a[mid - 1] != value)) return mid;
      else high = mid - 1;
    }
  }
  return -1;
}

如果求解的是第一个值等于给定值的元素，当a[mid]等于要查找的值时，需要确认一下这个a[mid]是不是第一个值等于给定值的元素。

找到与目标值相等的值时，要确认它的前一个数是否也等于目标值，如果相等，说明当前值肯定不是第一个，还得继续往前找。

2.查找最后一个值等于给定值的元素

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

与第一种类似，只需要检查后一个元素是否也等于目标值即可。

3.查找第一个大于等于给定值的元素

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] >= value) {
      if ((mid == 0) || (a[mid - 1] < value)) return mid;
      else high = mid - 1;
    } else {
      low = mid + 1;
    }
  }
  return -1;
}

类似的，只需要检查前一个数是否小于指定值。

4.查找最后一个小于等于给定值的元素

检查后一个数是否大于指定值。

public int bsearch7(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

---

如何快速定位出一个IP地址的归属地？

如果IP区间与归属地的对应关系不经常更新，可以先预处理这12万条数据，让其按照起始IP从小到大排序。将IP地址可以转化为32位的整型数。可以将起始地址，按照对应的整型值的大小关系，从小到大进行排序。

然后可将这个问题转化为第四种变形问题“在有序数组中，查找最后一个小于等于某个给定值的元素”。

先通过二分查找，找到最后一个起始IP小于等于这个IP的IP区间，然后，检查这个IP是否在这个IP区间内，如果在，我们就取出对应的归属地显示；如果不在，就返回未查找到。

二分查找更适合用在“近似”查找问题，在这类问题上，二分查找的优势更加明显。

易错细节：终止条件、区间上下界更新方法、返回值选择。