【牛客 - 剑指offer / 快速幂】JZ16 数值的整数次方 两种方案（直接运算、快速幂） Java实现

---

剑指offer题解汇总 Java实现

https://blog.csdn.net/guliguliguliguli/article/details/126089434

本题链接

知识分类篇 - 位运算 - JZ16 数值的整数次方

题目

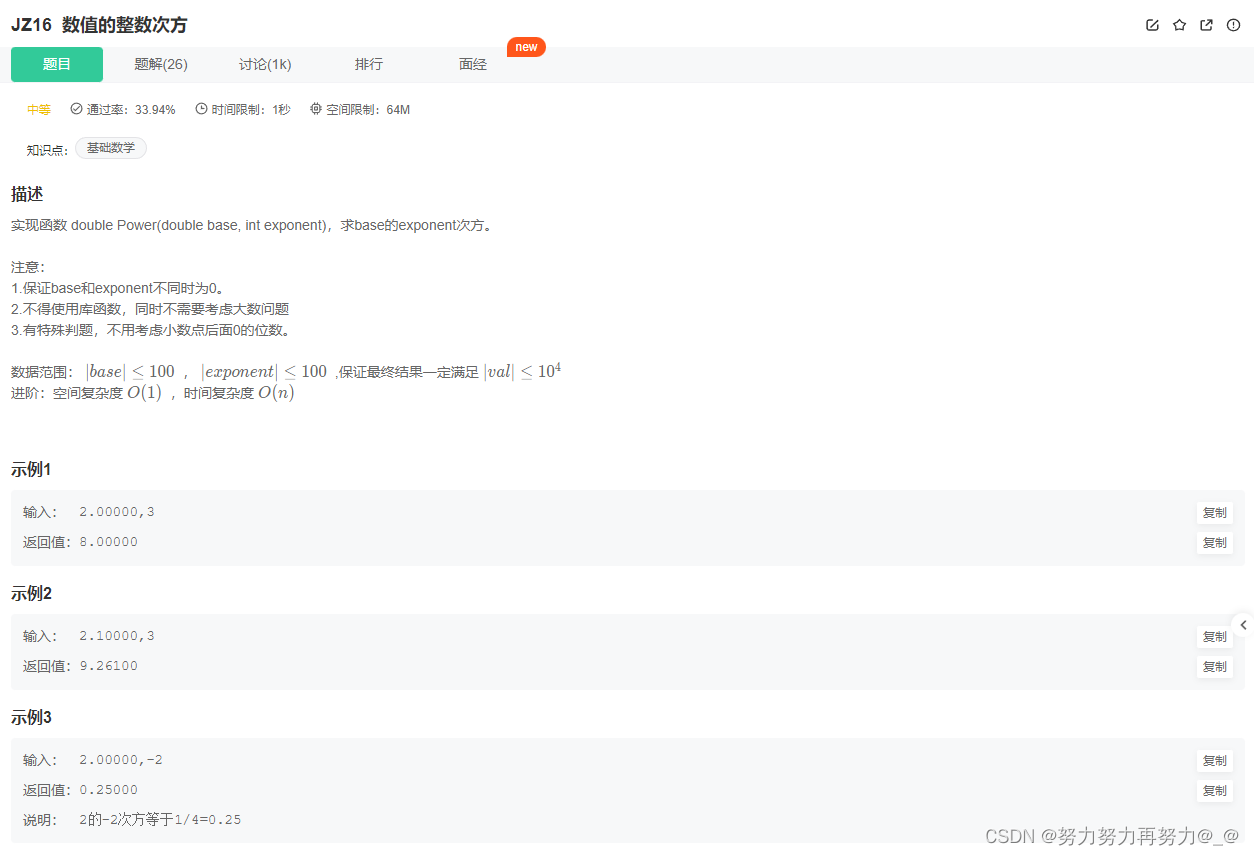
思路 & 代码

直接运算（最朴素思想、最直接）

按照exponent大于0，等于0，小于0分为三种情况讨论

• exponent > 0，直接循环，乘以相同的次数即可
• exponent = 0，返回1.0
• exponent < 0，exponent的值取为它的相反数，按照 exponent > 0 的情况进行相同的处理，最后用1.0去除以循环相乘的结果

import java.util.*;

public class Solution {
    public double Power(double base, int exponent) {

        if (exponent == 0) {
            return 1.0;
        }
        double res = base;
        if (exponent > 0) {
            for (int i = 1; i < exponent; i++) {
                res *= base;
            }
            return res;
        }
        res = base;
        exponent = -exponent;
        for (int i = 1; i < exponent; i++) {
            res *= base;
        }
        return 1.0 / res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

上面的代码提交以后，显示运行结果正确，不过，在代码中for循环的部分重复写了两遍，显得有些冗余，可以对代码稍加改进，修改的地方在于：

• 如果 exponent < 0，那么exponent 取它的相反数，并且，base的值取为1 / base值，这样无论是exponent > 0 的情况还是 exponent < 0 的情况，只要使用一个for循环就可以了

$$\begin{gathered} exponent=-exponent \\ base=\frac{1}{base} \end{gathered}$$

import java.util.*;

public class Solution {
    public double Power(double base, int exponent) {

        if (exponent == 0) {
            return 1.0;
        }
        if (exponent < 0) {
            exponent = -exponent;
            base = 1.0 / base;
        }
        double res = base;
        for (int i = 1; i < exponent; i++) {
            res *= base;
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

快速幂

我这样理解快速幂，主要观察指数，主要找出指数的二进制形式上，哪些位置为1

9（1001） = $2^0+2^3$
14（1110）=$2^1+2^2+2^3$
比如，我们要求$x^{14}$
14是偶数，所以x赋值为$x^2$，14/2=7
7是奇数，所以，res=$x^2$，x赋值为$x^2\cdot x^2=x^4$，7/2=3
3是奇数，所以，res=$x^2\cdot x^4=x^6$ ，x赋值为$x^4\cdot x^4=x^8$，3/2=1
1是奇数，所以，res=$x^6\cdot x^8=x^{14}$，1/2=0，退出循环

import java.util.*;

public class Solution {
    public double Power(double base, int exponent) {

        if (exponent == 0) {
            return 1.0;
        }
        if (exponent < 0) {
            exponent = -exponent;
            base = 1.0 / base;
        }
        return quickPow(base, exponent);
    }

    public double quickPow(double base, int exponent) {
        double res = 1;
        while (exponent != 0) {
            //判断是否为奇数
            //是，进入if
            //否，直接跳过
            if ((exponent & 1) != 0) {
                res *= base;
            }
            base *= base;
            exponent >>= 1;
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30