线性代数 --- 向量的长度

 一个向量的长度的平方等于这个向量与这个向量自己的内积

从代数的角度定义向量的长度：

      正如我在另外一篇文章中（见本文底部的推荐链接）提到的，两个向量（这是默认是两个列向量）的内积，可以表示为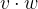也可以表示为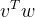。现在我们考虑一种特殊情形，现在我们有一个向量v=(1,2,3),那么这个向量自己和自己的内积是多少呢，他又代表了什么含义呢？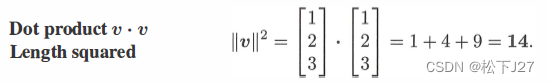

        一个向量的长度等于他和他自己的内积的平方根。这个向量与他自己是重合的，夹角为0。下面我们就给出一个向量的长度的正式定义：

---

从几何的角度定义向量的长度：

        在一个二维空间下，任意向量x的长度，是一个直角三角形的斜边。如下图所示：

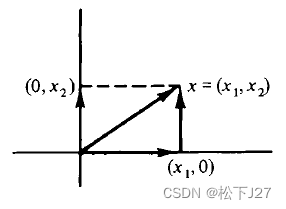
根据Pythagoras（毕达哥拉斯）定理，如果用符号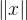表示斜边x的长度。则有：

 继续，在一个三维空间中，向量x=(x1,x2,x3)是一个长方体的对角线。如下图所示：

        这个对角线x的长度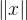，可以通过分别使用两次Pythagoras定理得到。第一次是应用该定理求得底面对角线OA=(x1,x2,0)的长度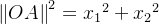。在OA，OB与竖棱(0,0,x3)所构成的直角三角形OAB中，斜边OB就是我们最终所要求的对角线x，这里我们再用一次Pythagoras定理，得：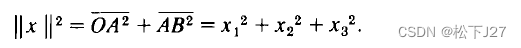

 以此类推，对于n维空间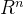中的向量x=(x1,x2,......,xn)有：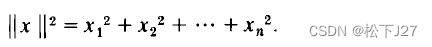

        即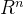，中的n维向量x的长度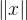等于它所有分量的平方和的平方根，取正号。这相当于是应用了n-1次Pythagoras定理。此外，对于一维向量，n=1的情况。该向量的长度等于其唯一一个分量的绝对值，也取正号。

---

个人笔记：

---

(全文完）

作者 --- 松下J27

格言摘抄：什么是女人？女人是形式逻辑的典范，是辩证逻辑的障碍。（《遥远的救世主》---豆豆）

推荐链接：线性代数 --- 向量的内积（点积）（个人学习笔记）_松下J27的博客-CSDN博客_线性代数内积

参考文献（鸣谢）：

1，《Introduction to Linear Algebra》,5th Edition - Gilbert Strang

 2，线性代数及其应用，侯自新，南开大学出版社，1990.

文中截图均来自于以上两本书中的插图。

  （配图与本文无关）

版权声明：所有的笔记，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27​