-
红黑树(Red Black Tree)
一、简介
红黑树是一种自平衡的二叉查找树。除了符合二叉查找树的基本特性外,还具有以下特性:
- 结点是红色或黑色。
- 根结点是黑色。
- 每个叶子结点都是黑色的空结点(NIL结点)。 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
- 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
图1就是一个红黑树的样例:
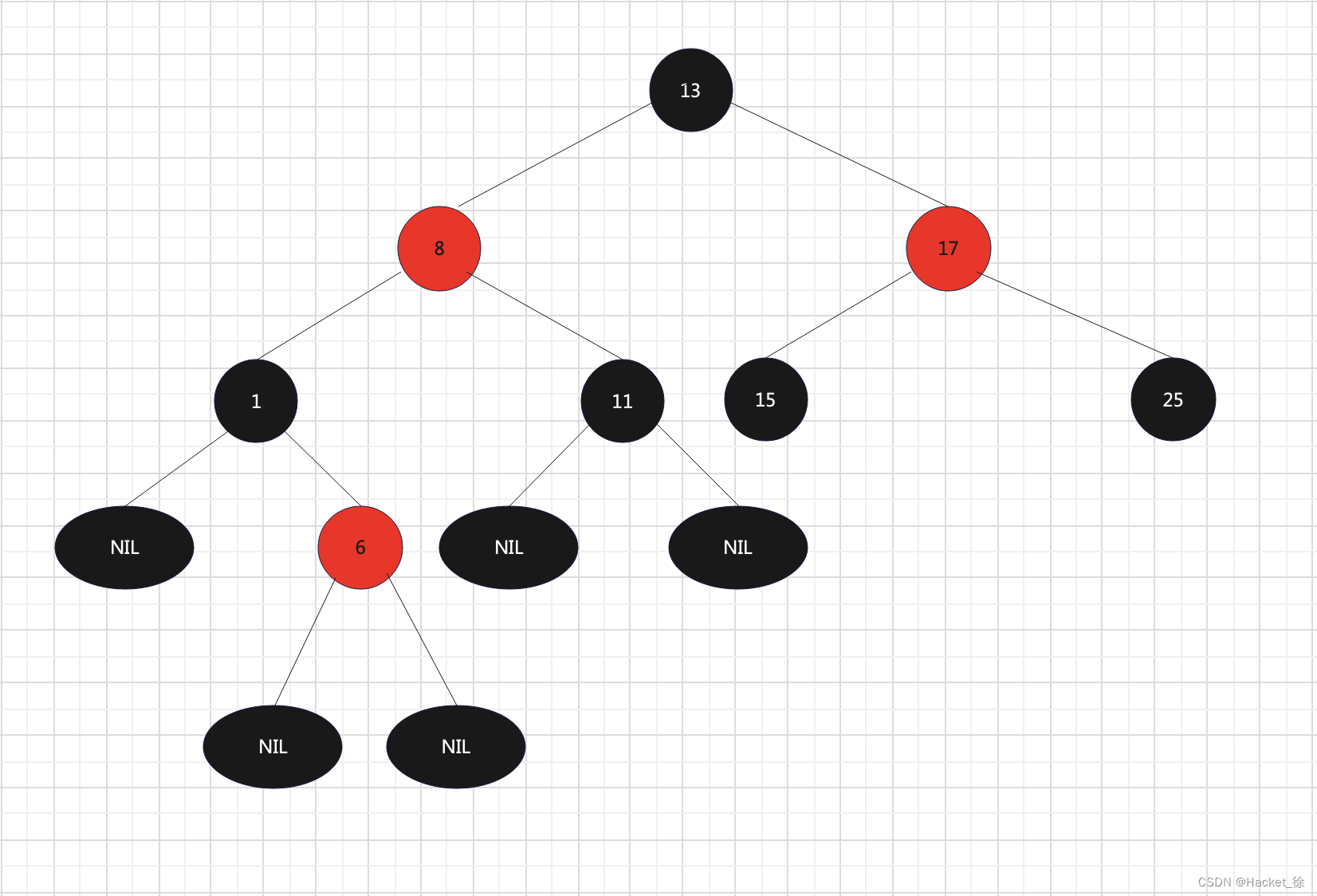
图1 - 红黑树示意图 二、相关操作
一、插入
正是因为这些条条框框的规则限制,才保证了红黑树的自平衡。红黑树从根到叶子的最长路径不超过最短路径的2倍。当插入或删除节点时,红黑树的规则又可能会被打破。这时候就需要进行调整来维持我们的规则。图2就是一种样例。
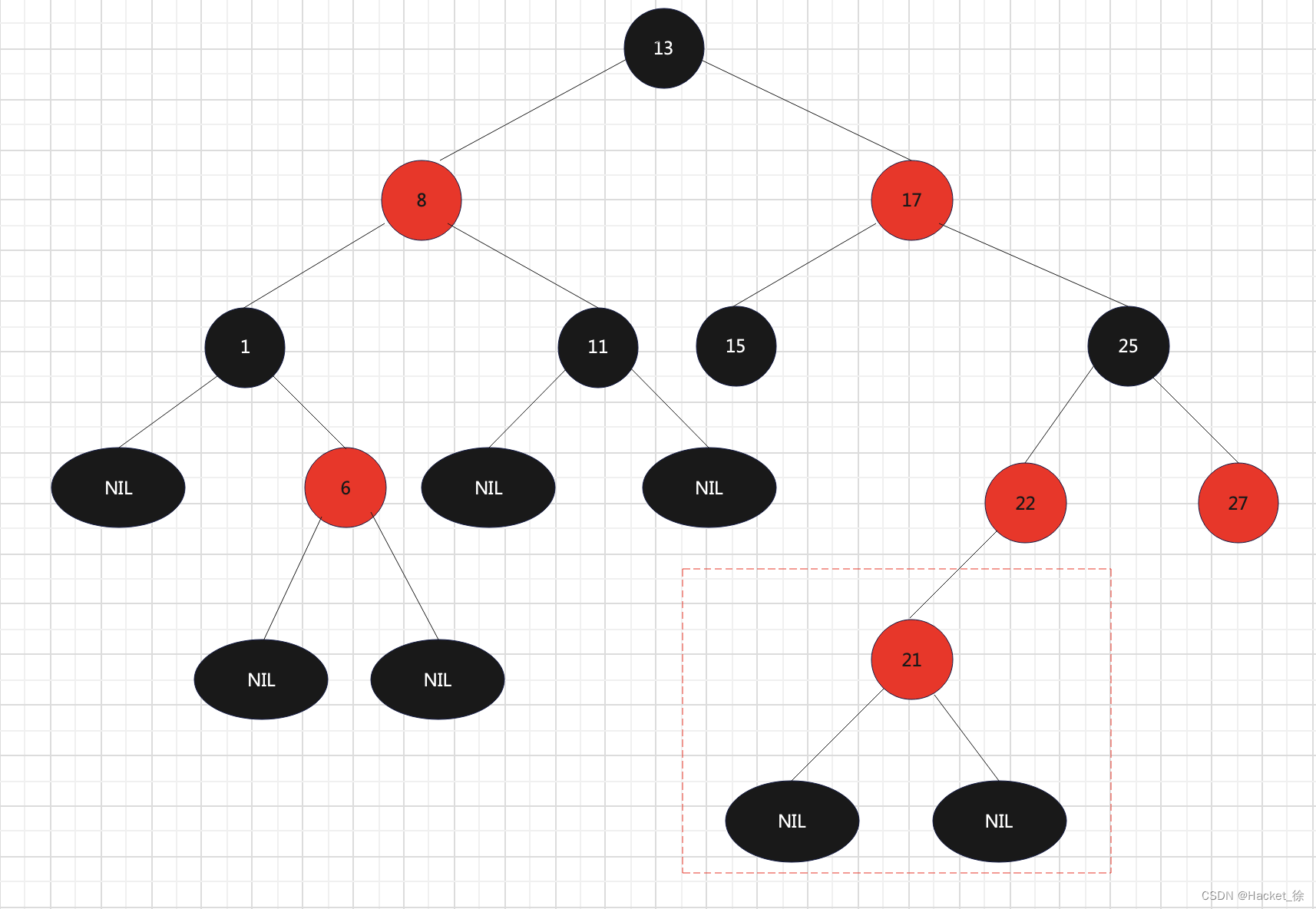
图2 - 打破规则的红黑树 那我们怎样才能调整红黑树,让它始终保持是红黑树呢?
调整方法有两种:变色或者旋转(包含左旋转和右旋转)。
变色
为重新符合红黑树的规则,我们只需要尝试把红色节点变为黑色节点,把黑色节点编程红色节点。
如图3所示,新叉入的y是红色节点,他的父节点x不符合规则,所以要把x从红色变成黑色。

图3 - 变色示意图 单仅仅一个变色,就可能导致凭空多出来一个黑色节点,所以我们需要对其他节点进行进一步调整,也就是旋转。
左旋转
逆时针旋转红黑树的两个节点,使父节点被右孩子节点代替,二孩子称为自己孩子的左孩子节点。说起来有点难,看图4能更好理解。

图4 - 左旋转示意图 其中,身为右孩子的y取代了x,x又变成了自己的左孩子。这就是左旋转。
右旋转
顺时针旋转红黑树的两个节点,使得父节点被左孩子节点取代,而自己成为自己的右孩子
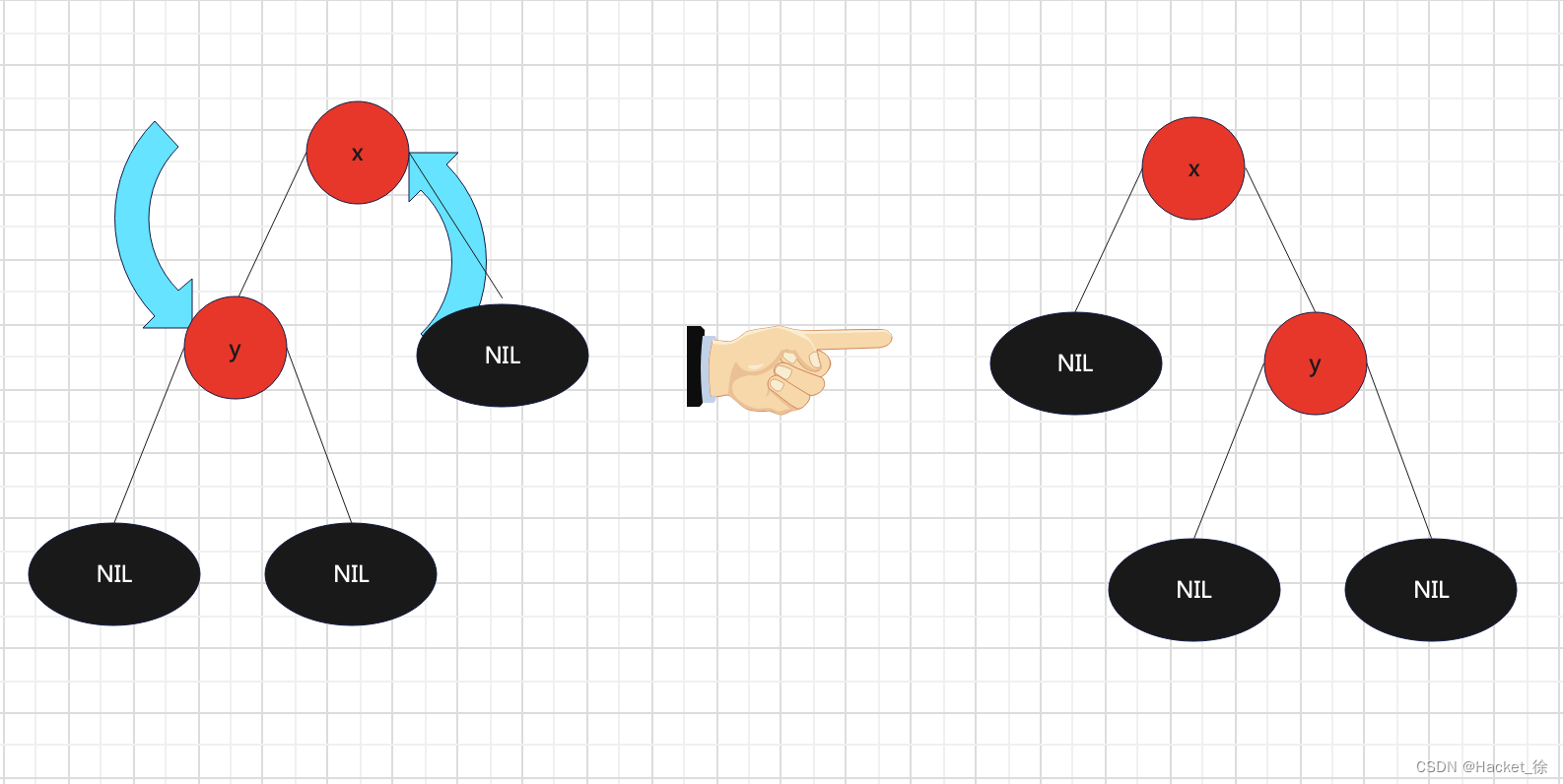
图5 - 右旋转示意图 图中,身为左孩子的y取代了x的位置,而x变成了自己的右孩子。这就是右旋转。
二、删除
对以上算法分析,若删除的结点是红色,则不做任何操作,红黑树的任何属性都不会被破坏;若删除的结点是黑色的,显然它所 在的路径上就少一个黑色结点,红黑树的性质就被破坏了,这时执行一个 Delete-Fixup()来修补这棵树。 一个结点被删除之后,一定 有一个它的结点代替了它的位置,即使是叶结点被删除后,也会有一个空结点来代替它的位置。 设指针 x 指向这个代替位置的结点,同时引入指向 x 兄弟的指针 w,这里均假设 x 是 x->parent 的左子结点,则 w 是 x->parent 的右子结点,如果实际遇到相反的情 况,只要把所有操作中的左、右互反一下就可以了。
三、代码实现
- #include
- #include
- #include "rbtree.h"
- #define rb_parent(r) ((r)->parent)
- #define rb_color(r) ((r)->color)
- #define rb_is_red(r) ((r)->color==RED)
- #define rb_is_black(r) ((r)->color==BLACK)
- #define rb_set_black(r) do { (r)->color = BLACK; } while (0)
- #define rb_set_red(r) do { (r)->color = RED; } while (0)
- #define rb_set_parent(r,p) do { (r)->parent = (p); } while (0)
- #define rb_set_color(r,c) do { (r)->color = (c); } while (0)
- /*
- * 创建红黑树,返回"红黑树的根"!
- */
- RBRoot* create_rbtree()
- {
- RBRoot *root = (RBRoot *)malloc(sizeof(RBRoot));
- root->node = NULL;
- return root;
- }
- /*
- * 前序遍历"红黑树"
- */
- static void preorder(RBTree tree)
- {
- printf("(");
- if(tree != NULL)
- {
- printf("%d%c", tree->key,tree->color?' ':'+');
- preorder(tree->left);
- preorder(tree->right);
- }
- printf(")");
- }
- void preorder_rbtree(RBRoot *root)
- {
- if (root)
- preorder(root->node);
- }
- /*
- * (递归实现)查找"红黑树x"中键值为key的节点
- */
- static Node* search(RBTree x, Type key)
- {
- if (x==NULL || x->key==key)
- return x;
- if (key < x->key)
- return search(x->left, key);
- else
- return search(x->right, key);
- }
- int rbtree_search(RBRoot *root, Type key)
- {
- if (root)
- return search(root->node, key)? 0 : -1;
- }
- /*
- * (非递归实现)查找"红黑树x"中键值为key的节点
- */
- static Node* iterative_search(RBTree x, Type key)
- {
- while ((x!=NULL) && (x->key!=key))
- {
- if (key < x->key)
- x = x->left;
- else
- x = x->right;
- }
- return x;
- }
- int iterative_rbtree_search(RBRoot *root, Type key)
- {
- if (root)
- return iterative_search(root->node, key) ? 0 : -1;
- }
- /*
- * 查找最小结点:返回tree为根结点的红黑树的最小结点。
- */
- static Node* minimum(RBTree tree)
- {
- if (tree == NULL)
- return NULL;
- while(tree->left != NULL)
- tree = tree->left;
- return tree;
- }
- int rbtree_minimum(RBRoot *root, int *val)
- {
- Node *node;
- if (root)
- node = minimum(root->node);
- if (node == NULL)
- return -1;
- *val = node->key;
- return 0;
- }
- /*
- * 查找最大结点:返回tree为根结点的红黑树的最大结点。
- */
- static Node* maximum(RBTree tree)
- {
- if (tree == NULL)
- return NULL;
- while(tree->right != NULL)
- tree = tree->right;
- return tree;
- }
- int rbtree_maximum(RBRoot *root, int *val)
- {
- Node *node;
- if (root)
- node = maximum(root->node);
- if (node == NULL)
- return -1;
- *val = node->key;
- return 0;
- }
- /*
- * 找结点(x)的后继结点。即,查找"红黑树中数据值大于该结点"的"最小结点"。
- */
- static Node* rbtree_successor(RBTree x)
- {
- // 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
- if (x->right != NULL)
- return minimum(x->right);
- // 如果x没有右孩子。则x有以下两种可能:
- // (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。
- // (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。
- Node* y = x->parent;
- while ((y!=NULL) && (x==y->right))
- {
- x = y;
- y = y->parent;
- }
- return y;
- }
- /*
- * 找结点(x)的前驱结点。即,查找"红黑树中数据值小于该结点"的"最大结点"。
- */
- static Node* rbtree_predecessor(RBTree x)
- {
- // 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
- if (x->left != NULL)
- return maximum(x->left);
- // 如果x没有左孩子。则x有以下两种可能:
- // (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。
- // (01) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。
- Node* y = x->parent;
- while ((y!=NULL) && (x==y->left))
- {
- x = y;
- y = y->parent;
- }
- return y;
- }
- /*
- * 对红黑树的节点(x)进行左旋转
- *
- * 左旋示意图(对节点x进行左旋):
- * px px
- * / /
- * x y
- * / \ --(左旋)--> / \ #
- * lx y x ry
- * / \ / \
- * ly ry lx ly
- *
- *
- */
- static void rbtree_left_rotate(RBRoot *root, Node *x)
- {
- // 设置x的右孩子为y
- Node *y = x->right;
- // 将 “y的左孩子” 设为 “x的右孩子”;
- // 如果y的左孩子非空,将 “x” 设为 “y的左孩子的父亲”
- x->right = y->left;
- if (y->left != NULL)
- y->left->parent = x;
- // 将 “x的父亲” 设为 “y的父亲”
- y->parent = x->parent;
- if (x->parent == NULL)//修改红黑树的根节点
- {
- //tree = y; // 如果 “x的父亲” 是空节点,则将y设为根节点
- root->node = y; // 如果 “x的父亲” 是空节点,则将y设为根节点
- }
- else
- {
- if (x->parent->left == x)
- x->parent->left = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
- else
- x->parent->right = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
- }
- // 将 “x” 设为 “y的左孩子”
- y->left = x;
- // 将 “x的父节点” 设为 “y”
- x->parent = y;
- }
- /*
- * 对红黑树的节点(y)进行右旋转
- *
- * 右旋示意图(对节点y进行左旋):
- * py py
- * / /
- * y x
- * / \ --(右旋)--> / \ #
- * x ry lx y
- * / \ / \ #
- * lx rx rx ry
- *
- */
- static void rbtree_right_rotate(RBRoot *root, Node *y)
- {
- // 设置x是当前节点的左孩子。
- Node *x = y->left;
- // 将 “x的右孩子” 设为 “y的左孩子”;
- // 如果"x的右孩子"不为空的话,将 “y” 设为 “x的右孩子的父亲”
- y->left = x->right;
- if (x->right != NULL)
- x->right->parent = y;
- // 将 “y的父亲” 设为 “x的父亲”
- x->parent = y->parent;
- if (y->parent == NULL)
- {
- //tree = x; // 如果 “y的父亲” 是空节点,则将x设为根节点
- root->node = x; // 如果 “y的父亲” 是空节点,则将x设为根节点
- }
- else
- {
- if (y == y->parent->right)
- y->parent->right = x; // 如果 y是它父节点的右孩子,则将x设为“y的父节点的右孩子”
- else
- y->parent->left = x; // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
- }
- // 将 “y” 设为 “x的右孩子”
- x->right = y;
- // 将 “y的父节点” 设为 “x”
- y->parent = x;
- }
- /*
- * 红黑树插入修正函数
- *
- * 在向红黑树中插入节点之后(失去平衡),再调用该函数;
- * 目的是将它重新塑造成一颗红黑树。
- *
- * 参数说明:
- * root 红黑树的根
- * node 插入的结点 // 对应《算法导论》中的z
- */
- static void rbtree_insert_fixup(RBRoot *root, Node *node)
- {
- Node *parent, *gparent;
- // 若“父节点存在,并且父节点的颜色是红色”
- while ((parent = rb_parent(node)) && rb_is_red(parent))
- {
- gparent = rb_parent(parent);
- //若“父节点”是“祖父节点的左孩子”
- if (parent == gparent->left)
- {
- // Case 1条件:叔叔节点是红色
- {
- Node *uncle = gparent->right;
- if (uncle && rb_is_red(uncle))//没有节点进入该分支,如何构造?
- {
- rb_set_black(uncle);
- rb_set_black(parent);
- rb_set_red(gparent);
- node = gparent;
- continue;
- }
- }
- // Case 2条件:叔叔是黑色,且当前节点是右孩子,叔叔不存在,也认为是黑色
- if (parent->right == node)//插入80节点时,先左旋,后右旋
- {
- Node *tmp;
- rbtree_left_rotate(root, parent);
- tmp = parent;
- parent = node;
- node = tmp;
- }
- // Case 3条件:叔叔是黑色,且当前节点是左孩子。
- rb_set_black(parent);//旋转前设置好颜色
- rb_set_red(gparent);//旋转前设置好颜色
- rbtree_right_rotate(root, gparent);
- }
- else//若父节点是祖父节点的右孩子
- {
- // Case 1条件:叔叔节点是红色
- {
- Node *uncle = gparent->left;//当插入60时,调整颜色即可,调整颜色后不符合红黑树,递归进行
- if (uncle && rb_is_red(uncle))
- {
- rb_set_black(uncle);
- rb_set_black(parent);
- rb_set_red(gparent);
- node = gparent;
- continue;//继续进行调整
- }
- }
- // Case 2条件:叔叔是黑色,且当前节点是左孩子,插入30时,先右旋,后左旋
- if (parent->left == node)
- {
- Node *tmp;
- rbtree_right_rotate(root, parent);
- tmp = parent;
- parent = node;
- node = tmp;
- }
- // Case 3条件:叔叔是黑色,且当前节点是右孩子。
- rb_set_black(parent);//旋转前设置好颜色
- rb_set_red(gparent);//旋转前设置好颜色
- rbtree_left_rotate(root, gparent);
- }
- }
- // 将根节点设为黑色
- rb_set_black(root->node);
- }
- /*
- * 添加节点:将节点(node)插入到红黑树中
- *
- * 参数说明:
- * root 红黑树的根
- * node 插入的结点 // 对应《算法导论》中的z
- */
- static void rbtree_insert(RBRoot *root, Node *node)
- {
- Node *y = NULL;
- Node *x = root->node;
- // 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。
- while (x != NULL)
- {
- y = x;
- if (node->key < x->key)
- x = x->left;
- else
- x = x->right;
- }
- rb_parent(node) = y;//找到父节点并把要插入节点的父节点的指针修改
- //修改父节点的子节点指针
- if (y != NULL)
- {
- if (node->key < y->key)
- y->left = node; // 情况2:若“node所包含的值” < “y所包含的值”,则将node设为“y的左孩子”
- else
- y->right = node; // 情况3:(“node所包含的值” >= “y所包含的值”)将node设为“y的右孩子”
- }
- else
- {
- root->node = node; // 情况1:若y是空节点,则将node设为根
- }
- // 2. 设置节点的颜色为红色
- node->color = RED;
- // 3. 将它重新修正为一颗二叉查找树
- rbtree_insert_fixup(root, node);
- }
- /*
- * 创建结点
- *
- * 参数说明:
- * key 是键值。
- * parent 是父结点。
- * left 是左孩子。
- * right 是右孩子。
- */
- static Node* create_rbtree_node(Type key, Node *parent, Node *left, Node* right)
- {
- Node* p;
- if ((p = (Node *)malloc(sizeof(Node))) == NULL)
- return NULL;
- p->key = key;
- p->left = left;
- p->right = right;
- p->parent = parent;
- p->color = BLACK; // 默认为黑色
- return p;
- }
- /*
- * 新建结点(节点键值为key),并将其插入到红黑树中
- *
- * 参数说明:
- * root 红黑树的根
- * key 插入结点的键值
- * 返回值:
- * 0,插入成功
- * -1,插入失败
- */
- int insert_rbtree(RBRoot *root, Type key)
- {
- Node *node; // 新建结点
- // 不允许插入相同键值的节点。
- // (若想允许插入相同键值的节点,注释掉下面两句话即可!)
- if (search(root->node, key) != NULL)
- return -1;
- // 如果新建结点失败,则返回。
- if ((node=create_rbtree_node(key, NULL, NULL, NULL)) == NULL)
- return -1;
- rbtree_insert(root, node);
- return 0;
- }
- /*
- * 红黑树删除修正函数
- *
- * 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
- * 目的是将它重新塑造成一颗红黑树。
- *
- * 参数说明:
- * root 红黑树的根
- * node 待修正的节点
- */
- static void rbtree_delete_fixup(RBRoot *root, Node *node, Node *parent)
- {
- Node *other;
- while ((!node || rb_is_black(node)) && node != root->node)
- {
- if (parent->left == node)
- {
- other = parent->right;
- if (rb_is_red(other))
- {
- // Case 1: x的兄弟w是红色的
- rb_set_black(other);
- rb_set_red(parent);
- rbtree_left_rotate(root, parent);
- other = parent->right;
- }
- if ((!other->left || rb_is_black(other->left)) &&
- (!other->right || rb_is_black(other->right)))
- {
- // Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
- rb_set_red(other);
- node = parent;
- parent = rb_parent(node);
- }
- else
- {
- if (!other->right || rb_is_black(other->right))
- {
- // Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
- rb_set_black(other->left);
- rb_set_red(other);
- rbtree_right_rotate(root, other);
- other = parent->right;
- }
- // Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
- rb_set_color(other, rb_color(parent));
- rb_set_black(parent);
- rb_set_black(other->right);
- rbtree_left_rotate(root, parent);
- node = root->node;
- break;
- }
- }
- else
- {
- other = parent->left;
- if (rb_is_red(other))
- {
- // Case 1: x的兄弟w是红色的
- rb_set_black(other);
- rb_set_red(parent);
- rbtree_right_rotate(root, parent);
- other = parent->left;
- }
- if ((!other->left || rb_is_black(other->left)) &&
- (!other->right || rb_is_black(other->right)))
- {
- // Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
- rb_set_red(other);
- node = parent;
- parent = rb_parent(node);
- }
- else
- {
- if (!other->left || rb_is_black(other->left))
- {
- // Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
- rb_set_black(other->right);
- rb_set_red(other);
- rbtree_left_rotate(root, other);
- other = parent->left;
- }
- // Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
- rb_set_color(other, rb_color(parent));
- rb_set_black(parent);
- rb_set_black(other->left);
- rbtree_right_rotate(root, parent);
- node = root->node;
- break;
- }
- }
- }
- if (node)
- rb_set_black(node);
- }
- /*
- * 删除结点
- *
- * 参数说明:
- * tree 红黑树的根结点
- * node 删除的结点
- */
- void rbtree_delete(RBRoot *root, Node *node)
- {
- Node *child, *parent;
- int color;
- // 被删除节点的"左右孩子都不为空"的情况。
- if ( (node->left!=NULL) && (node->right!=NULL) )
- {
- // 被删节点的后继节点。(称为"取代节点")
- // 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
- Node *replace = node;
- // 获取后继节点
- replace = replace->right;
- while (replace->left != NULL)
- replace = replace->left;
- // "node节点"不是根节点(只有根节点不存在父节点)
- if (rb_parent(node))
- {
- if (rb_parent(node)->left == node)
- rb_parent(node)->left = replace;
- else
- rb_parent(node)->right = replace;
- }
- else
- // "node节点"是根节点,更新根节点。
- root->node = replace;
- // child是"取代节点"的右孩子,也是需要"调整的节点"。
- // "取代节点"肯定不存在左孩子!因为它是一个后继节点。
- child = replace->right;
- parent = rb_parent(replace);
- // 保存"取代节点"的颜色
- color = rb_color(replace);
- // "被删除节点"是"它的后继节点的父节点"
- if (parent == node)
- {
- parent = replace;
- }
- else
- {
- // child不为空
- if (child)
- rb_set_parent(child, parent);
- parent->left = child;
- replace->right = node->right;
- rb_set_parent(node->right, replace);
- }
- replace->parent = node->parent;
- replace->color = node->color;
- replace->left = node->left;
- node->left->parent = replace;
- if (color == BLACK)
- rbtree_delete_fixup(root, child, parent);
- free(node);
- return ;
- }
- if (node->left !=NULL)
- child = node->left;
- else
- child = node->right;
- parent = node->parent;
- // 保存"取代节点"的颜色
- color = node->color;
- if (child)
- child->parent = parent;
- // "node节点"不是根节点
- if (parent)
- {
- if (parent->left == node)
- parent->left = child;
- else
- parent->right = child;
- }
- else
- root->node = child;
- if (color == BLACK)
- rbtree_delete_fixup(root, child, parent);
- free(node);
- }
- /*
- * 删除键值为key的结点
- *
- * 参数说明:
- * tree 红黑树的根结点
- * key 键值
- */
- void delete_rbtree(RBRoot *root, Type key)
- {
- Node *z, *node;
- if ((z = search(root->node, key)) != NULL)
- rbtree_delete(root, z);
- }
- /*
- * 销毁红黑树
- */
- static void rbtree_destroy(RBTree tree)
- {
- if (tree==NULL)
- return ;
- if (tree->left != NULL)
- rbtree_destroy(tree->left);
- if (tree->right != NULL)
- rbtree_destroy(tree->right);
- free(tree);
- }
- void destroy_rbtree(RBRoot *root)
- {
- if (root != NULL)
- rbtree_destroy(root->node);
- free(root);
- }
- /**
- * C语言实现的红黑树(Red Black Tree)
- *
- * @author skywang
- * @date 2013/11/18
- */
- #define CHECK_INSERT 1 // "插入"动作的检测开关(0,关闭;1,打开)
- #define CHECK_DELETE 1 // "删除"动作的检测开关(0,关闭;1,打开)
- #define LENGTH(a) ( (sizeof(a)) / (sizeof(a[0])) )
- void main()
- {
- int a[] = {10, 40, 30, 60, 90, 70, 20, 50, 80};
- int i, ilen=LENGTH(a);
- RBRoot *root=NULL;
- root = create_rbtree();
- printf("== 原始数据: ");
- for(i=0; iprintf("%d ", a[i]);printf("\n");for(i=0; i{insert_rbtree(root, a[i]);#if CHECK_INSERTprintf("== 添加节点: %d\n", a[i]);printf("\n");#endif}printf("\t\\tree"); preorder_rbtree(root); printf("\n**********************\n");if (rbtree_minimum(root, &i)==0)printf("== 最小值: %d\n", i);if (rbtree_maximum(root, &i)==0)printf("== 最大值: %d\n", i);printf("\n");#endifdelete_rbtree(root, 80);printf("== 删除节点: %d\n", 80);printf("\t\\tree"); preorder_rbtree(root); printf("\n********删除节点**************\n");destroy_rbtree(root);}
感谢阅读!
-
相关阅读:
session和cookie的区别
SpringBoot定义优雅全局统一Restful API 响应框架六
mysql忘记密码无法登录
208. 实现 Trie (前缀树)
利用iptable实现ssh端口复用后门
java计算机毕业设计HTML5互动游戏新闻网站设计与实现源码+数据库+系统+lw文档
CSS语法介绍与CSS选择器
win11和虚拟机上的ubuntu系统共享文件夹
Codeforces Round 895 div3 | JorbanS
浅述安防视频可视化场景中TSINGSEE青犀AI智能化应用的分析
- 原文地址:https://blog.csdn.net/weixin_46522531/article/details/126630477
