-
(01)ORB-SLAM2源码无死角解析-(56) 闭环线程→计算Sim3:理论推导(1)求解s,t
讲解关于slam一系列文章汇总链接:史上最全slam从零开始,针对于本栏目讲解的(01)ORB-SLAM2源码无死角解析链接如下(本文内容来自计算机视觉life ORB-SLAM2 课程课件):
(01)ORB-SLAM2源码无死角解析-(00)目录_最新无死角讲解:https://blog.csdn.net/weixin_43013761/article/details/123092196
文末正下方中心提供了本人 联系方式, 点击本人照片即可显示 W X → 官方认证 {\color{blue}{文末正下方中心}提供了本人 \color{red} 联系方式,\color{blue}点击本人照片即可显示WX→官方认证} 文末正下方中心提供了本人联系方式,点击本人照片即可显示WX→官方认证
一、前言
原论文 \color{red} 原论文 原论文 Closed-form solution of absolute orientation using unit quaternions
上一篇博客,对 ComputeSim3() 进行了整体的讲解,大致明白了了 sim3 的作用。但是应该如何求解相似变换(Similarity Transformation)呢?在上一篇博客中提到:
T = [ R t 0 1 ] T s = [ s R t 0 1 ] (01) \color{Green} \tag{01} \mathbf T=\left[Rt01\right]~~~~~~~~~~~~~~~~~~Ts=\left[sRt01\right] T=⎣ ⎡R0t1⎦ ⎤ Ts=⎣ ⎡sR0t1⎦ ⎤(01)左边为欧式变换矩阵,右边的是相似变换矩阵,可以很明显的知道仅仅相差一个尺度因子 s s s,当 s = 1 s=1 s=1的时候,相似变换就成了欧式变换。总的来说计算Sim3 实际就是计算这三个参数:旋转 R \mathbf R R 平移 t \mathbf t t 尺度因子 s s s。理论来说计算Sim3需要3对不共线的点对即可求解。为什么三对不共线点就可以求解?那么下面来推导一下:( 1 ) : \color{blue}(1): (1):假设坐标系1下有三个不共线三维点 P 1 P_1 P1, P 2 P_2 P2, P 3 P_3 P3,他们分别和坐标系2下的三个不共线三维点 Q 1 Q_1 Q1, Q 2 Q_2 Q2, Q 3 Q_3 Q3 一一匹配,如下图所示:
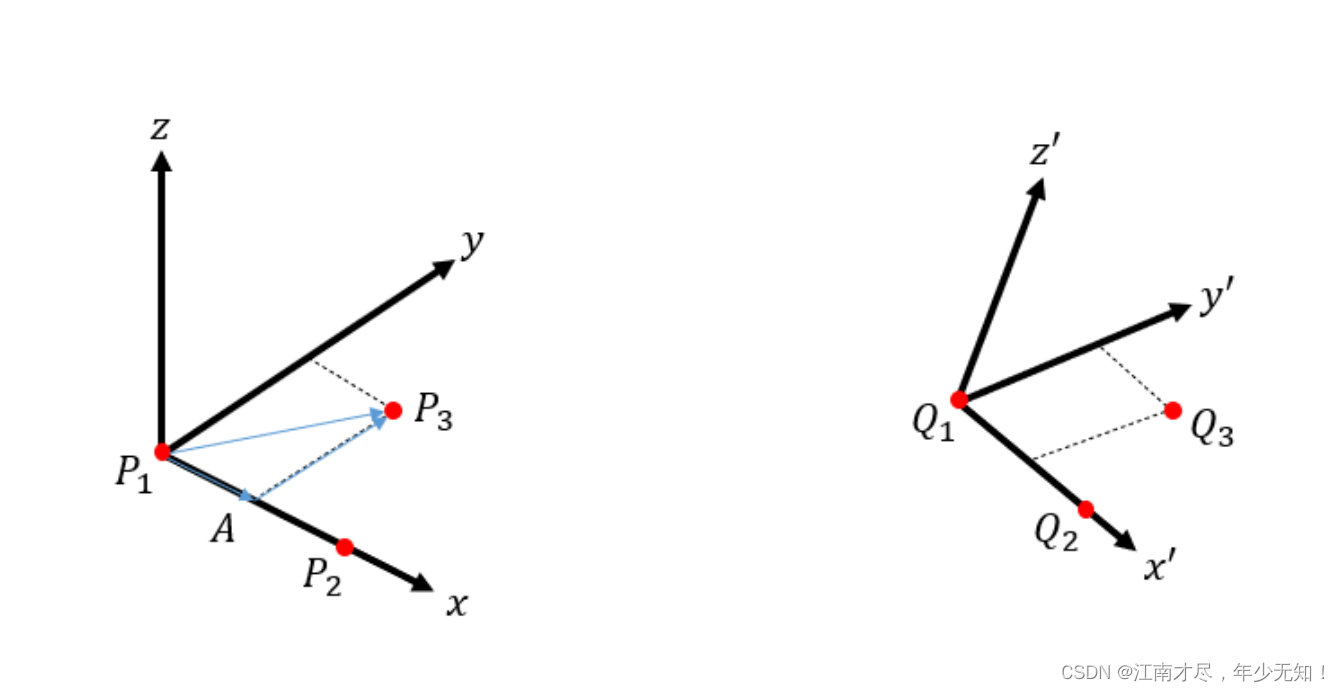
( 2 ) : \color{blue}(2): (2):首先,我们根据坐标系1下的三个不共线三维点来构造一个新的坐标系。沿着 x x x 上的单位向量 x ^ \hat{x} x^: x = P 2 − P 1 x ^ = x ∥ x ∥ (02) \color{Green} \tag{02} x=P_{2}-P_{1} ~~~~~~~~~~~~~~~~~~~~~~~~~~~\hat{x}=\frac{x}{\|x\|} x=P2−P1 x^=∥x∥x(02)沿着 y y y 轴的单位向量 y ^ \hat{y} y^: y = A P 3 → = P 1 P 3 → − P 1 A → = ( P 3 − P 1 ) − [ ( P 3 − P 1 ) x ^ ] x ^ y ^ = y ∥ y ∥ (03) \color{Green} \tag{03} y =\overrightarrow{A P_{3}} =\overrightarrow{P_{1} P_{3}}-\overrightarrow{P_{1} A} =\left(P_{3}-P_{1}\right)-\left[\left(P_{3}-P_{1}\right) \hat{x}\right] \hat{x}~~~~~~~~~~~~~~~~~~\hat{y} =\frac{y}{\|y\|} y=AP3=P1P3−P1A=(P3−P1)−[(P3−P1)x^]x^ y^=∥y∥y(03)沿着 z z z 轴的单位向量 z ^ \hat{z} z^: z ^ = x ^ × y ^ (04) \color{Green} \tag{04} \hat{z}=\hat{x} \times \hat{y} z^=x^×y^(04)
( 3 ) : \color{blue}(3): (3):同理,我们对于坐标系2下的 Q 1 Q_1 Q1, Q 2 Q_2 Q2, Q 3 Q_3 Q3 也可以得到沿着3个坐标轴的单位向量 x ′ ^ , y ′ ^ , z ′ ^ \hat{x^{\prime}}, \hat{y^{\prime}}, \hat{z^{\prime}} x′^,y′^,z′^。
( 4 ) : \color{blue}(4): (4):我们现在要计算 坐标系1 到 坐标系2 的旋转,记坐标系单位向量构成的基底矩阵为: M 1 = [ x ^ , y ^ , z ^ ] M 2 = [ x ′ ^ , y ′ ^ , z ′ ^ ] (05) \color{Green} \tag{05} \mathbf M_{1}=[\hat{x}, \hat{y}, \hat{z}] ~~~~~~~~~~~~~~~~~~~\mathbf M_{2}=\left[\hat{x^{\prime}}, \hat{y^{\prime}}, \hat{z^{\prime}}\right] M1=[x^,y^,z^] M2=[x′^,y′^,z′^](05)
( 5 ) : \color{blue}(5): (5): 假设坐标系1下有一个向量 v 1 v_1 v1,他在坐标系2下记为 v 2 v_2 v2,因为向量本身没没有变化,根据坐标系定义有: M 1 v 1 = M 2 v 2 ⇒ v 2 = M 2 T M 1 v 1 (06) \color{Green} \tag{06} \mathbf M_{1} v_{1} =\mathbf M_{2} v_{2}~~~~~~\Rightarrow~~~~~~v_{2} =\mathbf M_{2}^{T} \mathbf M_{1} v_{1} M1v1=M2v2 ⇒ v2=M2TM1v1(06)那么从坐标系1到坐标系2的旋转就是
R = M 2 T M 1 (07) \color{Green} \tag{07} R=\mathbf M_{2}^{T} \mathbf M_{1} R=M2TM1(07)( 6 ) : \color{blue}(6): (6):看起来好像没什么问题,但是实际上我们不会这样使用,因为存在如下问题:
①这个旋转的结果和选择点的顺序关系密切,我们分别让不同的点做坐标系原点,得到的结果不同。
②这种情况不适用于匹配点大于3个的情况。
因此实际上我们不会使用以上方法。我们通常能够拿到远大于3个的三维匹配点对,我们会使用最小二乘法来得到更稳定、更精确的结果。提示: \color{red}提示: 提示:如果熟悉EPnP,阅读过之前的 (01)ORB-SLAM2源码无死角解析-(37) EPnP 算法原理详解→理论基础一:控制点选取、透视投影约束,那么理解接下来的推导应该是比较简单的。
二、计算SIM3平移
( 1 ) : \color{blue}(1): (1):假设得到了 n > 3 n>3 n>3 组匹配的三维点,分别记为 { P i } , { Q i } \{P_i\},\{Q_i\} {Pi},{Qi},其中 i = 1 , . . . , n i=1,...,n i=1,...,n 我们的目的是对于
每对匹配点,找到如下的变换关系: Q i = s R P i + t (08) \color{Green} \tag{08} Q_{i}=s \mathbf R P_{i}+\mathbf t Qi=sRPi+t(08)其中 s s s 是尺度因子, R \mathbf R R 是旋转, t \mathbf t t 是平移。
( 2 ) : \color{blue}(2): (2):如果数据是没有任何噪音的理想数据,理论上我们可以找到满足上述关系的尺度因子、旋转和平移。但实际上数据是不可避免会有噪音和误差,所以我们转换思路,定义一个误差 e i e_i ei,我们的目的就是寻找合适的尺度因子、旋转和平移,使得它在所有数据上的误差最小。 e i = Q i − s R P i − t min s , R , t ∑ i = 1 n ∥ e i ∥ 2 = min s , R , t ∑ i = 1 n ∥ Q i − s R P i − t ∥ 2 (09) \color{Green} \tag{09} ei=Qi−sRPi−tmins,R,tn∑i=1‖ei‖2=mins,R,tn∑i=1‖Qi−sRPi−t‖2eis,R,tmini=1∑n∥ei∥2=Qi−sRPi−t=s,R,tmini=1∑n∥Qi−sRPi−t∥2(09) ( 3 ) : \color{blue}(3): (3):在开始求解之前,我们先定义两个三维点集合中所有三维点的均值(或者称为质心、重心) P ˉ = 1 n ∑ i = 1 n P i Q ˉ = 1 n ∑ i = 1 n Q i (10) \color{Green} \tag{10} \bar{P}=\frac{1}{n} \sum_{i=1}^{n} P_{i}~~~~~~~~~~~~~~~~~~~~~\bar{Q}=\frac{1}{n} \sum_{i=1}^{n} Q_{i} Pˉ=n1i=1∑nPi Qˉ=n1i=1∑nQi(10)我们对每个三维点 P i , Q i P_i,Q_i Pi,Qi 分别减去均值,得到去中心化后的坐标 P i ′ , Q i ′ P'_i,Q'_i Pi′,Qi′ 则有 P i ′ = P i − P ˉ Q i ′ = Q i − Q ˉ (11) \color{Green} \tag{11} P_{i}^{\prime}=P_{i}-\bar{P}~~~~~~~~~~~~~~~~~~~~~~Q_{i}^{\prime}=Q_{i}-\bar{Q} Pi′=Pi−Pˉ Qi′=Qi−Qˉ(11) ∑ i = 1 n P i ′ = ∑ i = 1 n ( P i − P ˉ ) = ∑ i = 1 n P i − n P ˉ = 0 ∑ i = 1 n Q i ′ = ∑ i = 1 n ( Q i − Q ˉ ) = ∑ i = 1 n Q i − n Q ˉ = 0 (12) \color{Green} \tag{12}\sum_{i=1}^{n} P_{i}^{\prime}=\sum_{i=1}^{n}\left(P_{i}-\bar{P}\right)=\sum_{i=1}^{n} P_{i}-n \bar{P}=0\\\sum_{i=1}^{n} Q_{i}^{\prime}=\sum_{i=1}^{n}\left(Q_{i}-\bar{Q}\right)=\sum_{i=1}^{n} Q_{i}-n \bar{Q}=0 i=1∑nPi′=i=1∑n(Pi−Pˉ)=i=1∑nPi−nPˉ=0i=1∑nQi′=i=1∑n(Qi−Qˉ)=i=1∑nQi−nQˉ=0(12)上面的结论很重要,我们在后面推导的时候要使用。
( 4 ) : \color{blue}(4): (4):下面开始推导我们的误差方程:
∑ i = 1 n ∥ e i ∥ 2 = ∑ i = 1 n ∥ Q i − s R P i − t ∥ 2 = ∑ i = 1 n ∥ Q i ′ + Q ˉ − s R P i ′ − s R P ˉ − t ∥ 2 = ∑ i = 1 n ∥ ( Q i ′ − s R P i ′ ) + ( Q ˉ − s R P ˉ − t ) ⏟ t 0 ∥ 2 = ∑ i = 1 n ∥ ( Q i ′ − s R P i ′ ) ∥ 2 + 2 t 0 ∑ i = 1 n ( Q i ′ − s R P i ′ ) + n ∥ t 0 ∥ 2 (13) \color{Green} \tag{13} n∑i=1‖ei‖2=n∑i=1‖Qi−sRPi−t‖2=n∑i=1‖Q′i+ˉQ−sRP′i−sRˉP−t‖2=n∑i=1‖(Q′i−sRP′i)+(ˉQ−sRˉP−t)⏟t0‖2=n∑i=1‖(Q′i−sRP′i)‖2+2t0n∑i=1(Q′i−sRP′i)+n‖t0‖2i=1∑n∥ei∥2=i=1∑n∥Qi−sRPi−t∥2=i=1∑n∥ ∥Qi′+Qˉ−sRPi′−sRPˉ−t∥ ∥2=i=1∑n∥(Qi′−sRPi′)+t0 (Qˉ−sRPˉ−t)∥2=i=1∑n∥(Qi′−sRPi′)∥2+2t0i=1∑n(Qi′−sRPi′)+n∥t0∥2(13)为了推导不显得那样臃肿,其中我们简记 t 0 = Q ˉ − s R P ˉ − t \mathbf t_{0}=\bar{Q}-s \mathbf R \bar{P}-\mathbf t t0=Qˉ−sRPˉ−t
( 5 ) : \color{blue}(5): (5):根据前面(12)式的推导可得等式右边中间项 ∑ i = 1 n ( Q i ′ − s R P i ′ ) = ∑ i = 1 n Q i ′ − s R ∑ i = 1 n P i ′ = 0 (14) \color{Green} \tag{14} \sum_{i=1}^{n}\left(Q_{i}^{\prime}-s \mathbf R P_{i}^{\prime}\right)=\sum_{i=1}^{n} Q_{i}^{\prime}-s \mathbf R \sum_{i=1}^{n} P_{i}^{\prime}=0 i=1∑n(Qi′−sRPi′)=i=1∑nQi′−sRi=1∑nPi′=0(14)这样前面误差方程(13)式可以化简为: ∑ i = 1 n ∥ e i ∥ 2 = ∑ i = 1 n ∥ ( Q i ′ − s R P i ′ ) ∥ 2 + n ∥ t 0 ∥ 2 (15) \color{Green} \tag{15} \sum_{i=1}^{n}\left\|e_{i}\right\|^{2}=\sum_{i=1}^{n}\left\|\left(Q_{i}^{\prime}-s \mathbf R P_{i}^{\prime}\right)\right\|^{2}+n\left\| \mathbf t_{0}\right\|^{2} i=1∑n∥ei∥2=i=1∑n∥(Qi′−sRPi′)∥2+n∥t0∥2(15)
( 6 ) : \color{blue}(6): (6):等式右边的两项都是大于等于0的平方项,并且只有第二项里的 t 0 \mathbf t_{0} t0 和我们要求的平移 t \mathbf t t 有关,所以当 t 0 = 0 时 \mathbf t_{0}=0时 t0=0时 ,我们可以得到平移的最优解 t ∗ t^* t∗:
t 0 = Q ˉ − s R P ˉ − t = 0 ⇒ t ∗ = Q ˉ − s R P ˉ (16) \color{Green} \tag{16} \mathbf t_{0}=\bar{Q}-s \mathbf R \bar{P}-\mathbf t=0~~~~~~~~~\Rightarrow~~~~~~~~\mathbf t^{*}=\bar{Q}-s \mathbf R \bar{P} t0=Qˉ−sRPˉ−t=0 ⇒ t∗=Qˉ−sRPˉ(16)也就是说我们知道了旋转 R \mathbf R R 和尺度 s s s 就能根据三维点均值做差得到平移 t \mathbf t t 了,注意这里平移的方向是 { P i } → { Q i } \{P_i\}→\{Q_i\} {Pi}→{Qi}。 R \mathbf R R 的求解在下一篇博客中讲解,接着来看看如何求解 s s s。
三、计算SIM3尺度
( 1 ) : \color{blue}(1): (1):针对于误差函数(15)式,因为第二项与 s s s没有关系,所以可以进一步简化为:
∑ i = 1 n ∥ e i ∥ 2 = ∑ i = 1 n ∥ Q i ′ − s R P i ′ ∥ 2 = ∑ i = 1 n ∥ Q i ′ ∥ 2 − 2 s ∑ i = 1 n Q i ′ R P i ′ + s 2 ∑ i = 1 n ∥ R P i ′ ∥ 2 (17) \color{Green} \tag{17} n∑i=1‖ei‖2=n∑i=1‖Q′i−sRP′i‖2=n∑i=1‖Q′i‖2−2sn∑i=1Q′iRP′i+s2n∑i=1‖RP′i‖2i=1∑n∥ei∥2=i=1∑n∥Qi′−sRPi′∥2=i=1∑n∥Qi′∥2−2si=1∑nQi′RPi′+s2i=1∑n∥RPi′∥2(17)( 2 ) : \color{blue}(2): (2):由于向量的模长不受旋转的影响,所以 ∥ R P i ′ ∥ 2 = ∥ P i ′ ∥ 2 \left\|\mathbf R P_{i}^{\prime}\right\|^{2}=\left\|P_{i}^{\prime}\right\|^{2} ∥RPi′∥2=∥Pi′∥2,为了后续更加清晰的表示,我们用简单的符号代替上述式子里的部分内容,所以有 ∑ i = 1 n ∥ e i ∥ 2 = ∑ i = 1 n ∥ Q i ′ ∥ 2 ⏟ S Q − 2 s ∑ i = 1 n Q i ′ R P i ′ ⏟ D + s 2 ∑ i = 1 n ∥ P i ′ ∥ 2 ⏟ S P = S Q − 2 s D + s 2 S P (18) \color{Green} \tag{18} n∑i=1‖ei‖2=n∑i=1‖Q′i‖2⏟SQ−2sn∑i=1Q′iRP′i⏟D+s2n∑i=1‖P′i‖2⏟SP=SQ−2sD+s2SP
i=1∑n∥ei∥2=SQ i=1∑n∥Qi′∥2−2sD i=1∑nQi′RPi′+s2SP i=1∑n∥Pi′∥2=SQ−2sD+s2SP(18)
( 3 ) : \color{blue}(3): (3):由于 R \mathbf R R 是已知的(下一篇博客会讲解其具体来源),所以很容易看出来上面是一个以 为自变量的一元二次方程,要使得该方程误差最小,我们可以得到此时尺度 s s s 的取值: s = D S P = ∑ i = 1 n Q i ′ R P i ′ ∑ i = 1 n ∥ P i ′ ∥ 2 (19) \color{Green} \tag{19} s=\frac{D}{S_{P}}=\frac{\sum_{i=1}^{n} Q_{i}^{\prime} \mathbf R P_{i}^{\prime}}{\sum_{i=1}^{n}\left\|P_{i}^{\prime}\right\|^{2}} s=SPD=∑i=1n∥Pi′∥2∑i=1nQi′RPi′(19)ORB–SLAM2和3里都是使用上述公式求尺度。注意这里尺度的方向是 { P i } → { Q i } \{P_i\}→\{Q_i\} {Pi}→{Qi},但是,到这里还存在一个问题,我们对 P , Q P,Q P,Q 做个调换后得到 ∑ i = 1 n P i ′ R T Q i ′ ∑ i = 1 n ∥ Q i ′ ∥ 2 ≠ 1 s (20) \color{Green} \tag{20} \frac{\sum_{i=1}^{n} P_{i}^{\prime} \mathbf R^{T} Q_{i}^{\prime}}{\sum_{i=1}^{n}\left\|Q_{i}^{\prime}\right\|^{2}} \neq \frac{1}{s} ∑i=1n∥Qi′∥2∑i=1nPi′RTQi′=s1(20)我们看到尺度并不具备对称性,也就是从 { P i } → { Q i } \{P_i\}→\{Q_i\} {Pi}→{Qi} 得到的尺度并不是从 { Q i } → { P i } \{Q_i\}→ \{P_i\} {Qi}→{Pi} 得到尺度的倒数,这也说明我们前面方法得到的尺度并不稳定。
( 4 ) : \color{blue}(4): (4):所以需要重新构造误差函数,使得我们得到 的尺度是对称的、稳定的。当然我们不用自己绞尽脑汁去构造,直接搬运论文里大佬的构造方法即可:
∑ i = 1 n ∥ e i ∥ 2 = ∑ i = 1 n ∥ 1 s Q i ′ − s R P i ′ ∥ 2 = 1 s ∑ i = 1 n ∥ Q i ′ ∥ 2 ⏟ S Q − 2 ∑ i = 1 n Q i ′ R P i ′ ⏟ D + s ∑ i = 1 n ∥ R P i ′ ∥ 2 ⏟ S P = 1 s S Q − 2 D + s S P = ( s S P − S Q s ) 2 + 2 ( S P S Q − D ) (21) \color{Green} \tag{21} n∑i=1‖ei‖2=n∑i=1‖1√sQ′i−√sRP′i‖2=1sn∑i=1‖Q′i‖2⏟SQ−2n∑i=1Q′iRP′i⏟D+sn∑i=1‖RP′i‖2⏟SP=1sSQ−2D+sSP=(√sSP−√SQs)2+2(SPSQ−D)i=1∑n∥ei∥2=i=1∑n∥ ∥s1Qi′−sRPi′∥ ∥2=s1SQ i=1∑n∥Qi′∥2−D 2i=1∑nQi′RPi′+sSP i=1∑n∥RPi′∥2=s1SQ−2D+sSP=(sSP−sSQ)2+2(SPSQ−D)(21)
( 5 ) : \color{blue}(5): (5):上面等式右边第一项只和尺度 s s s 有关的平方项,第二项和 s s s 无关,但是和旋转 R R R 有关,因此令第一项为 0,就能够得到最佳得尺度 s ∗ s^* s∗ s ∗ = S Q S P = ∑ i = 1 n ∥ Q i ′ ∥ 2 ∑ i = 1 n ∥ P i ′ ∥ 2 (22) \color{Green} \tag{22} s^{*}=\sqrt{\frac{S_{Q}}{S_{P}}}=\sqrt{\frac{\sum_{i=1}^{n}\left\|Q_{i}^{\prime}\right\|^{2}}{\sum_{i=1}^{n}\left\|P_{i}^{\prime}\right\|^{2}}} s∗=SPSQ=∑i=1n∥Pi′∥2∑i=1n∥Qi′∥2(22)同时,第二项里的 S p S_p Sp, S q S_q Sq 都是平方项,所以令第二项里的 D = ∑ i = 1 n Q i ′ R P i ′ D=\sum_{i=1}^{n} Q_{i}^{\prime} \mathbf R P_{i}^{\prime} D=∑i=1nQi′RPi′ 最大,可以使得剩下的误差函数最小。可以使得剩下的误差函数最小。
四、结语
从(22)式可以看出,其是一个对称结构,也就是说从 { P i } → { Q i } \{P_i\}→\{Q_i\} {Pi}→{Qi} 得到的尺度并是从 { Q i } → { P i } \{Q_i\}→ \{P_i\} {Qi}→{Pi} 得到尺度的倒数。这里我们总结下对称形式的优势:
①使得尺度的解和旋转、平移都无关
②反过来,旋转的确定不受数据选择不同的影响
③直观理解,尺度就是三维点到各自均值中心的距离之和。但是这里还遗留了一个待解决的问题,那就是求解平移 t \mathbf t t 的时候,需要用到旋转矩阵 R \mathbf R R, 那么下一篇博客,就来看看 R \mathbf R R 是如何求解的吧!
本文内容来自计算机视觉life ORB-SLAM2 课程课件 -
相关阅读:
02 C++STL之容器
(黑马C++)L01 C++概述
QTabBar实验
深度解读智能媒体服务的重组和进化
Springboot中的@Import注解~
【NoSQL】NoSQL之redis配置与优化(简单操作)
【RabbitMQ】——消息应答
golang并发编程基础
多线程面试相关知识点
【Spring】使用注解开发前提条件
- 原文地址:https://blog.csdn.net/weixin_43013761/article/details/126648996