【LeetCode】Day125-最接近的三数之和 & 电话号码的字母组合

题目1、最接近的三数之和

16. 最接近的三数之和【中等】

题解

15. 三数之和【中等】的同款，思路差不多，由于答案只有一个，还不需要去重了

class Solution {
    public int threeSumClosest(int[] nums, int target) {
        int minDis=Integer.MAX_VALUE,res=0,n=nums.length;
        Arrays.sort(nums);
        for(int i=0;i<n;i++){
            int L=i+1,R=n-1;
            while(L<R){
                int sum=nums[i]+nums[L]+nums[R];
                //如果恰好等于target,直接返回
                if(sum==target)
                    return sum;
                int dis=sum-target;
                if(Math.abs(dis)<minDis){
                    res=sum;
                    minDis=Math.abs(dis);
                }
                if(sum>=res)
                    R--;
                else if(sum<res)
                    L++;
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

时间复杂度：$O(n^2)$

空间复杂度：$O(logn)$，排序所需空间复杂度

题目2、电话号码的字母组合

17. 电话号码的字母组合【中等】

题解

硬做的话循环太多了，官解用了回溯法解决这道题

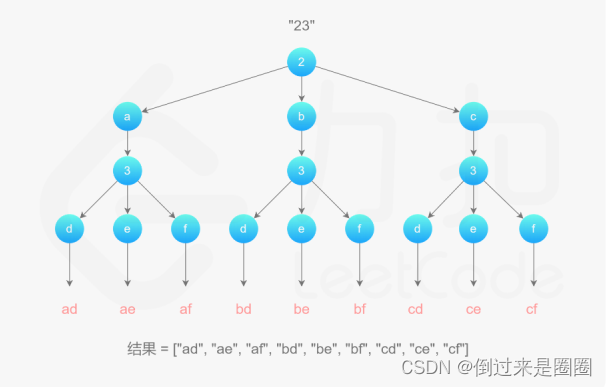
class Solution {
    String[] strs=new String[]{"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
    public List<String> letterCombinations(String digits) {
        List<String>res=new ArrayList<>();
        int n=digits.length();
        if(n==0)
            return res;
        backtrack(digits,0,new StringBuffer(),res);//res址传递
        return res;
    }
    public void backtrack(String digits,int index,StringBuffer combination,List<String>res){
        if(index==digits.length())
            res.add(combination.toString());//完成一种字母组合
        else{
            String digStr=strs[(digits.charAt(index)-'0')-2];//数字对应的字母串
            //遍历字母串
            for(int i=0;i<digStr.length();i++){
                combination.append(digStr.charAt(i));
                backtrack(digits,index+1,combination,res);
                combination.deleteCharAt(index);//回溯
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

时间复杂度：$O(3^m\times 4^n)$，其中 m 是输入中对应 3 个字母的数字个数（包括数字 2、3、4、5、6、8），n 是输入中对应 4 个字母的数字个数（包括数字 7、9），m+n是输入数字的总个数。当输入包含 m 个对应 3 个字母的数字和 n 个对应 4 个字母的数字时，不同的字母组合一共有 $3^m\times 4^n$种，需要遍历每一种字母组合。

空间复杂度：$O(m+n)$，哈希表的大小与输入无关，可以看成常数，递归调用层数最大为m+n。