-
数据结构学习笔记 5-1 单调队列(Monotone-Queue)与 LeetCode真题(Java)
喜欢该类型文章可以给博主点个关注,博主会持续输出此类型的文章,知识点很全面,再加上LeetCode的真题练习,每一个LeetCode题解我都写了详细注释,比较适合新手入门数据结构与算法,后续也会更新进阶的文章。
课件参考—开课吧《门徒计划》5-1 单调队列(Monotone-Queue)及经典问题(上)
前面我们学习过一些普通的数据结构:队列、栈,它们都是线性 简单的数据结构,没有涉及到什么操作的算法,但今天我们开始涉及一些稍微复杂的算法,单调队列对于普通队列的数据结构比起来稍微复杂了些,它会在原有队列的结构之上进行一些特殊的操作。
单调队列的题在面试中比较少见,所以今天的选题较少。
单调队列基础知识
我们用一个问题来引入单调队列的概念, R M Q RMQ RMQ 是一类问题的统称: R a n g e m a x / m i n q u e r y Range\ max/min\ query Range max/min query,查询区间范围内的最大值或者最小值。
就是查询给定区间的最值问题,有可能是最大值,有可能是最小值,在本文中全部认为是查询最小值。

最少记录几个元素,就可以满足 R M Q ( x , 7 ) RMQ(x,\ 7) RMQ(x, 7) 的任何需求? x x x 在 0 − 7 0-7 0−7 之间任意变化。
我们需要记录 4 4 4 个数字,下标分别为: 1 1 1、 4 4 4、 6 6 6、 7 7 7,就可以满足需求:
- R M Q ( 1 , 7 ) = > 记录下标为 1 的元素 ( 1 ) RMQ(1,\ 7) => 记录下标为1的元素(1) RMQ(1, 7)=>记录下标为1的元素(1)
- R M Q ( 2 , 7 ) = > 记录下标为 4 的元素 ( 2 ) RMQ(2,\ 7) => 记录下标为4的元素(2) RMQ(2, 7)=>记录下标为4的元素(2)
- R M Q ( 3 , 7 ) = > 记录下标为 4 的元素 ( 2 ) RMQ(3,\ 7) => 记录下标为4的元素(2) RMQ(3, 7)=>记录下标为4的元素(2)
- R M Q ( 4 , 7 ) = > 记录下标为 4 的元素 ( 2 ) RMQ(4,\ 7) => 记录下标为4的元素(2) RMQ(4, 7)=>记录下标为4的元素(2)
- R M Q ( 5 , 7 ) = > 记录下标为 6 的元素 ( 8 ) RMQ(5,\ 7) => 记录下标为6的元素(8) RMQ(5, 7)=>记录下标为6的元素(8)
- R M Q ( 6 , 7 ) = > 记录下标为 6 的元素 ( 8 ) RMQ(6,\ 7) => 记录下标为6的元素(8) RMQ(6, 7)=>记录下标为6的元素(8)
- R M Q ( 7 , 7 ) = > 记录下标为 7 的元素 ( 12 ) RMQ(7,\ 7) => 记录下标为7的元素(12) RMQ(7, 7)=>记录下标为7的元素(12)
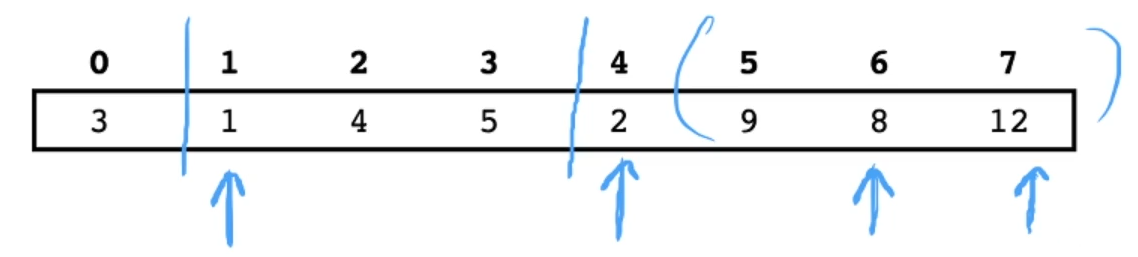
我们发现: 1 1 1 、 2 、2 、2、 8 8 8、 12 12 12,这 4 4 4 个数字单调递增,我们就把这个单调递增的序列叫做单调序列。
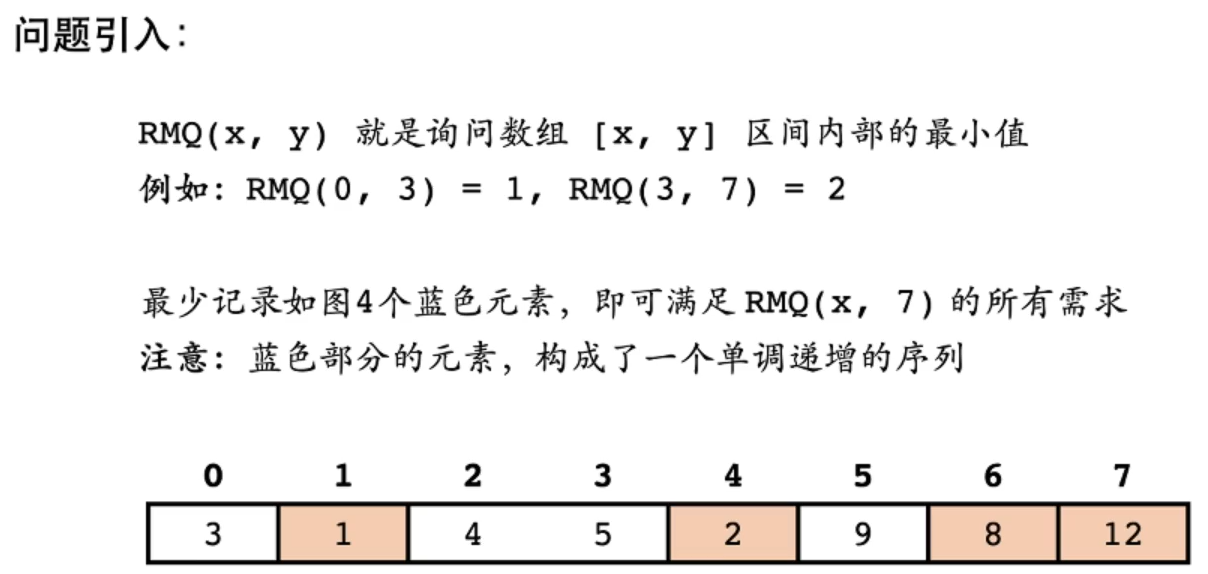
想要求得一个 R M Q ( x , y ) RMQ(x,\ y) RMQ(x, y), y y y 被固定时,就可以采用刚才得到的顺序,这就是一个单调队列。

单调队列—维护过程
单调队列的维护过程本质上就是一个滑动窗口的过程。
我们设置滑动窗口的大小为 3 3 3,此时队列中存入了 1 1 1 和 4 4 4,虽然 1 1 1 比 4 4 4 小,但后续窗口滑动会将 1 1 1 丢掉,为了保守起见也要把 4 4 4 存入。
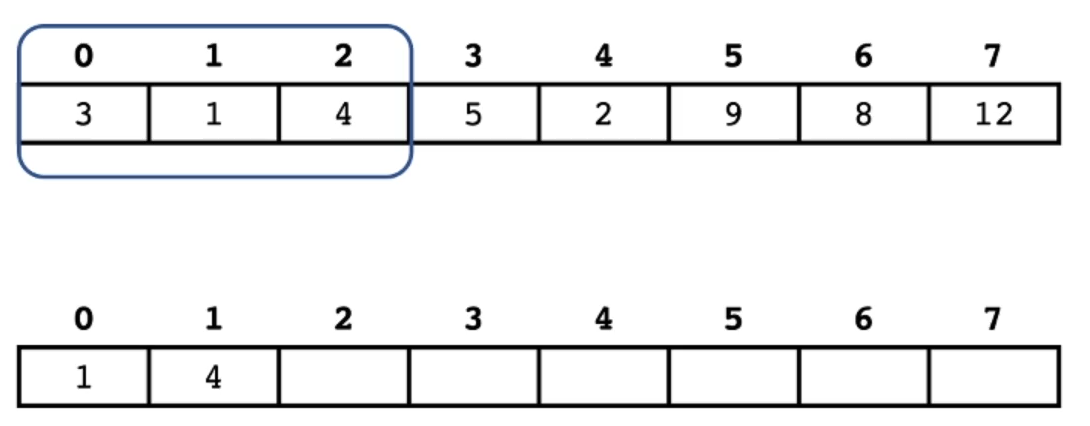
再把 5 5 5 存入。
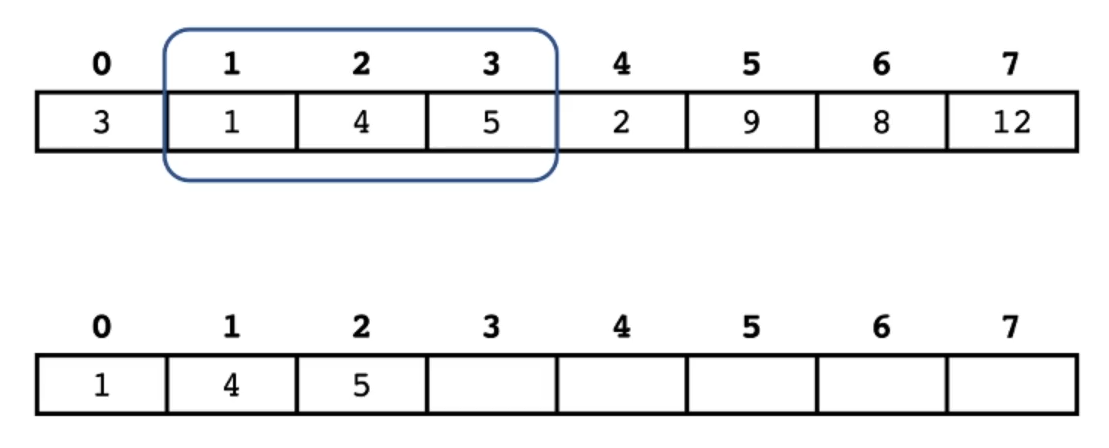
此时 1 1 1 已经不再窗口中,将它忽略,由于进来的 2 2 2 比 4 4 4、 5 5 5 都小,所以将 4 4 4、 5 5 5 移除队列,将 2 2 2 存入队列中。
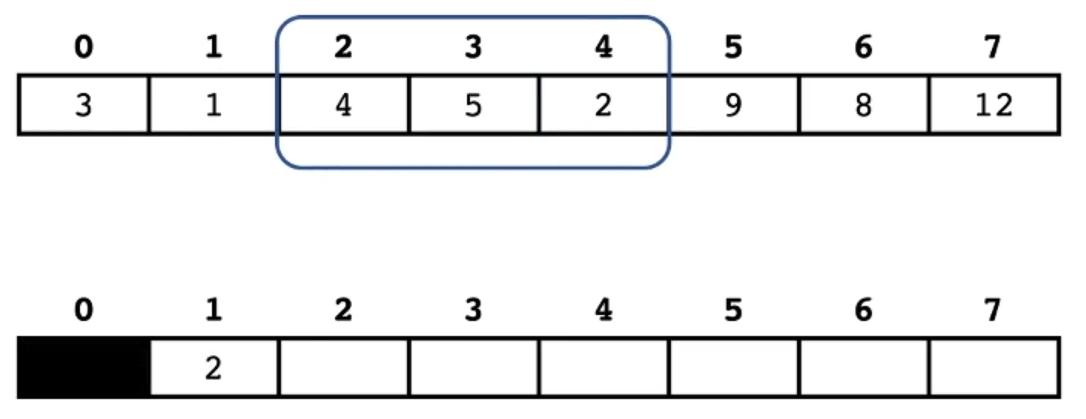
同理把 9 9 9 也存入。
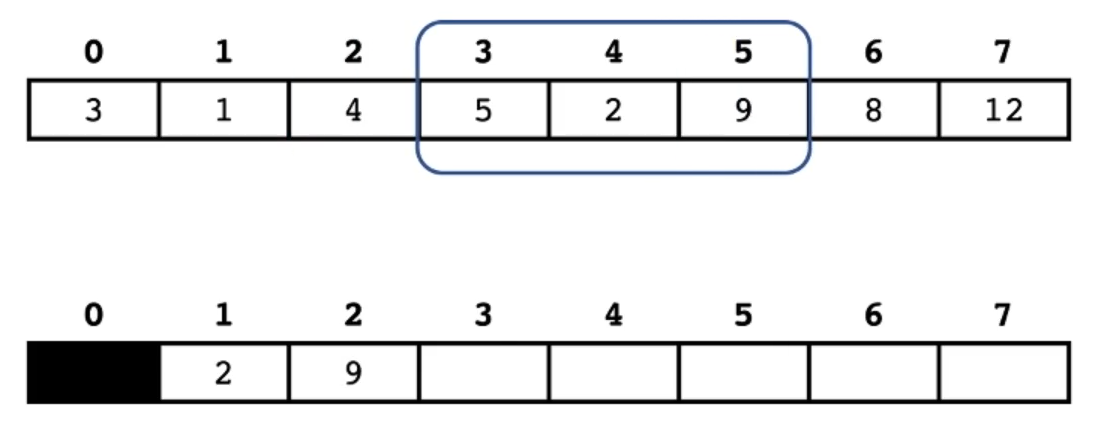
8 8 8 比 9 9 9 小,所以移除 9 9 9,加入 8 8 8。
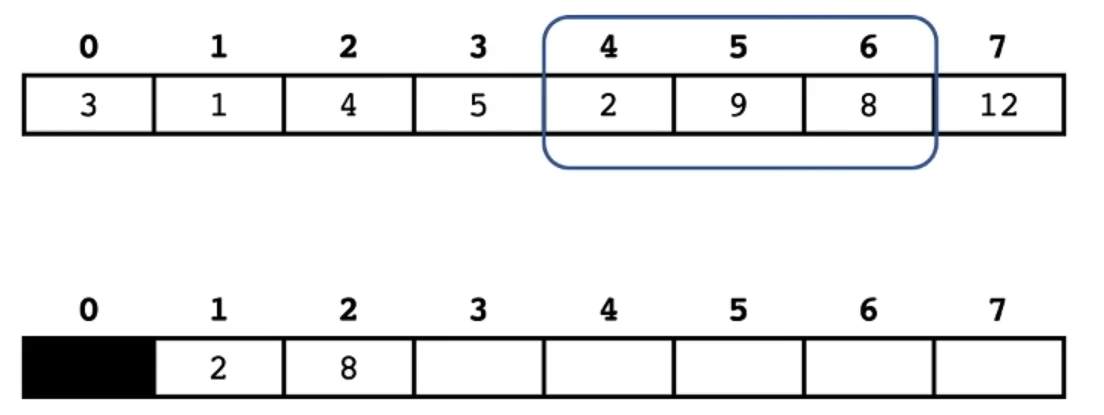
同理加入 12 12 12。
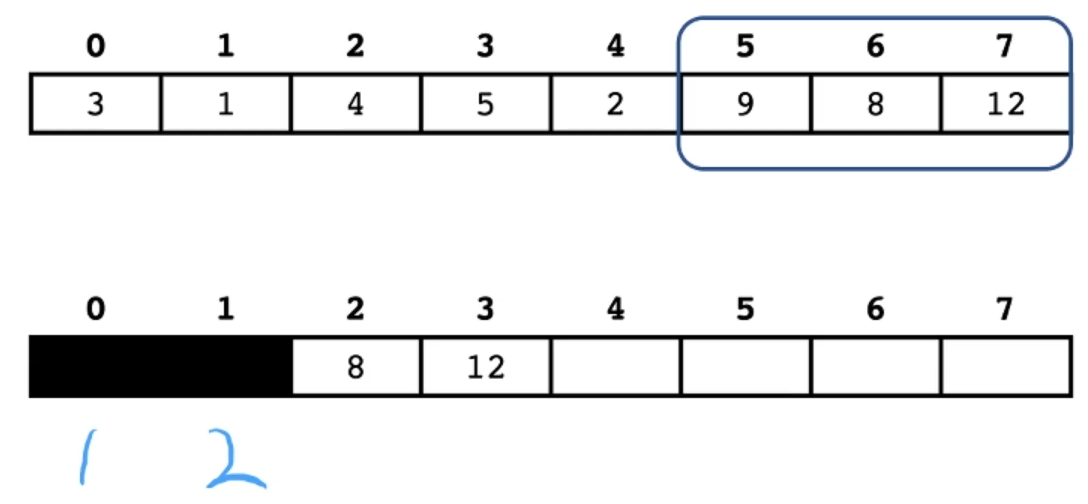
以上就是单调队列滑动的过程,那么单调队列的作用是什么呢?其实它就是在维护我们滑动窗口的最值。
只要单调队列中有元素,那么队首元素一定是滑动窗口的最小值,这样我们就可以快速得到在窗口滑动的过程中所有的最值问题。
单调队列总结
单调队列就是一种特殊的结构,解决窗口在滑动过程中的最值问题。
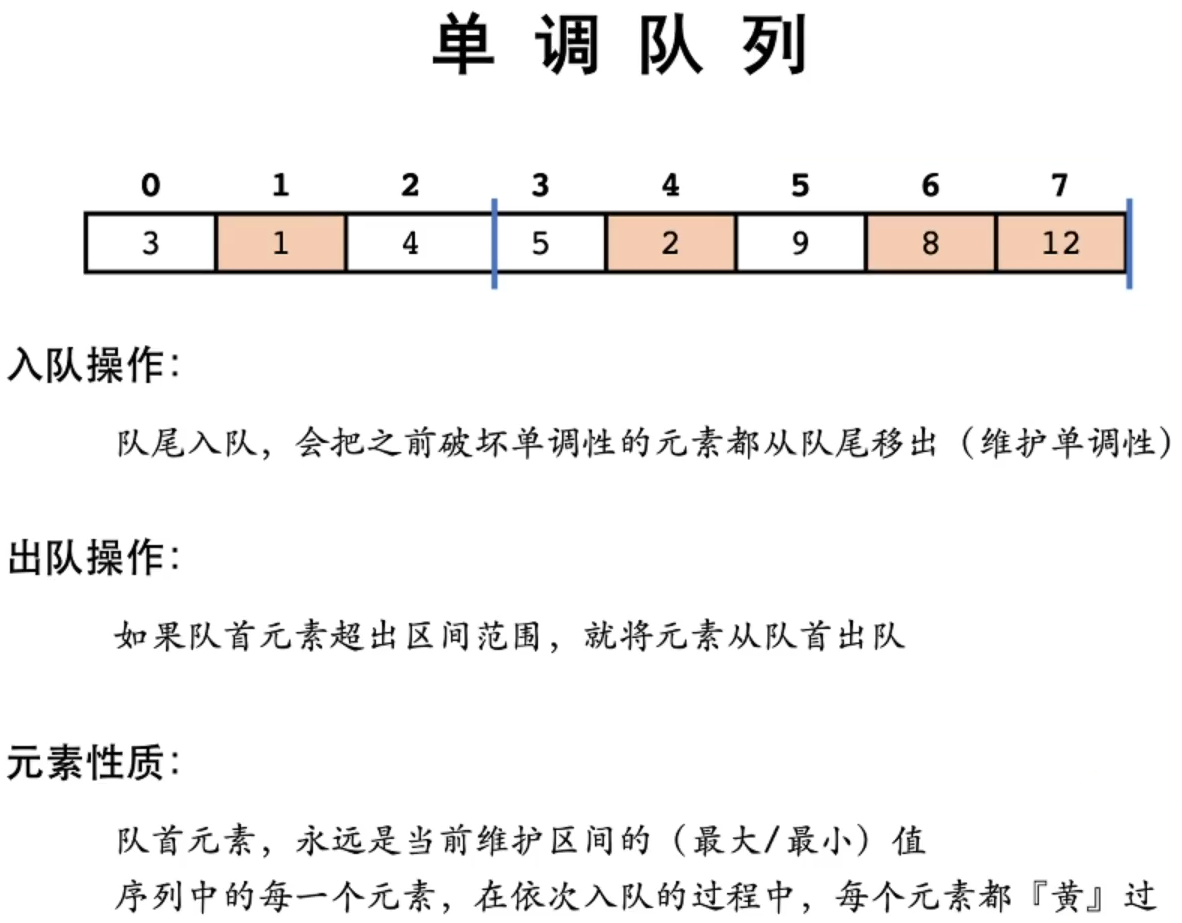
维护一个单调队列 存放窗口的最小值
import java.util.Deque; import java.util.LinkedList; import java.util.Scanner; public class Main { static final int N = 300010; static int[] arr = new int[N]; public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(), k = sc.nextInt(); // n为元素个数 k为滑动窗口大小 for (int i = 0; i < n; i++) arr[i] = sc.nextInt(); Deque<Integer> q = new LinkedList<>(); // 双端队列 // 最小值 for (int i = 0; i < n; i++) { // 如果队尾元素大于当前元素 则将队尾元素删除 放入当前元素 (保证单调性) while (!q.isEmpty() && arr[q.peekLast()] > arr[i]) q.pollLast(); q.offerLast(i); // 放入队尾 if (i - q.peekFirst() == k) q.removeFirst(); // 窗口满了 移除队首元素 if (i + 1 < k) continue; // 窗口未满 if (i + 1 > k) System.out.print(" "); // 规范输出 System.out.print(arr[q.peekFirst()]); } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
LeetCode真题
单调队列经典题目
LeetCode239. 滑动窗口最大值
难度:
hard别看是一道hard题,如果理解了单调队列,那么这道题就非常简单。
其实跟上面实现的代码一模一样,不过上面的代码是维护最小值,只需要把大于号换成小于号即可。
维护一个最大值的单调队列,队首元素永远是这个滑动窗口的最大值。
LeetCode题解:代码实现
LeetCode面试题59 - II. 队列的最大值
难度:
mid这道题就不一样了,并没有明确给我们一个序列以及滑动窗口的大小,需要我们自己定义一个队列并实现函数。
请定义一个队列并实现函数
max_value得到队列里的最大值,要求函数max_value、push_back和pop_front的均摊时间复杂度都是O(1)。这句话的意思就是让我们实现一个队列,具有的额外功能是瞬间得到该队列的最大值 M a x Max Max,也就是再额外维护一个单调队列。
该单调队列的队首元素永远是最大值,且队列递减。
LeetCode题解:代码实现
LeetCode862. 和至少为 K 的最短子数组
难度:
hard在数组中找到和大于等于 k k k 的长度最短的数组。
典型单调队列是找滑动窗口的极值,这道题是一个非典型单调队列。
首先我们预处理前缀和:
s[0] = 0, s[i] = a[0] + a[1] + ... + a[i];,枚举时枚举数组的右端点 i i i,我们需要在 i i i 前面找到一个 j j j,使得 S i − S j ⩾ k S_i-S_j \geqslant k Si−Sj⩾k,且 i − j i-j i−j 最小,对于每个 i i i 找到一个满足条件的 j j j,取一个 M i n Min Min 就是答案。怎么找呢?这就需要用到单调队列了。
假设 S i − S j 1 ⩾ k S_i-S_{j1} \geqslant k Si−Sj1⩾k,此时同样满足: S i − S j 2 ⩾ k S_i-S_{j2} \geqslant k Si−Sj2⩾k, S i − S j 3 ⩾ k S_i-S_{j3} \geqslant k Si−Sj3⩾k,那我们肯定会取 S j 3 S_{j3} Sj3 这个值作为首选,因为数组长度最短。
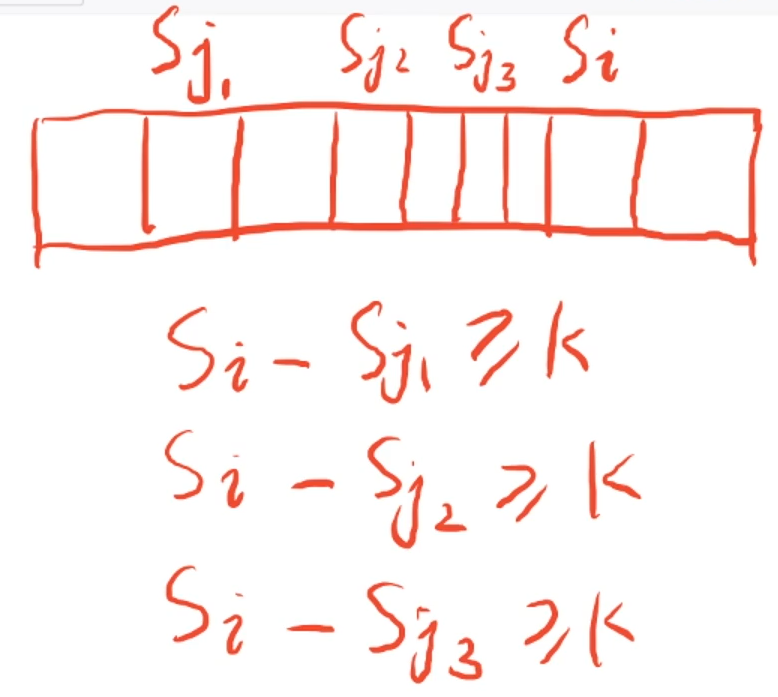
我们发现,此时我们只需要维护 S j S_j Sj 即可,目前为止的正确答案是 S j 3 S_{j3} Sj3,当遍历到 S i S_i Si 后面的 S i + 1 S_{i+1} Si+1 时,只需要跟 S j 3 S_{j3} Sj3 进行判断即可, S j 2 S_{j2} Sj2 和 S j 1 S_{j1} Sj1 显然不是更优的答案,所以不再需要记录这两个值,只需要存一个离我们最近的值,这个特性恰巧符合了单调队列的特性。
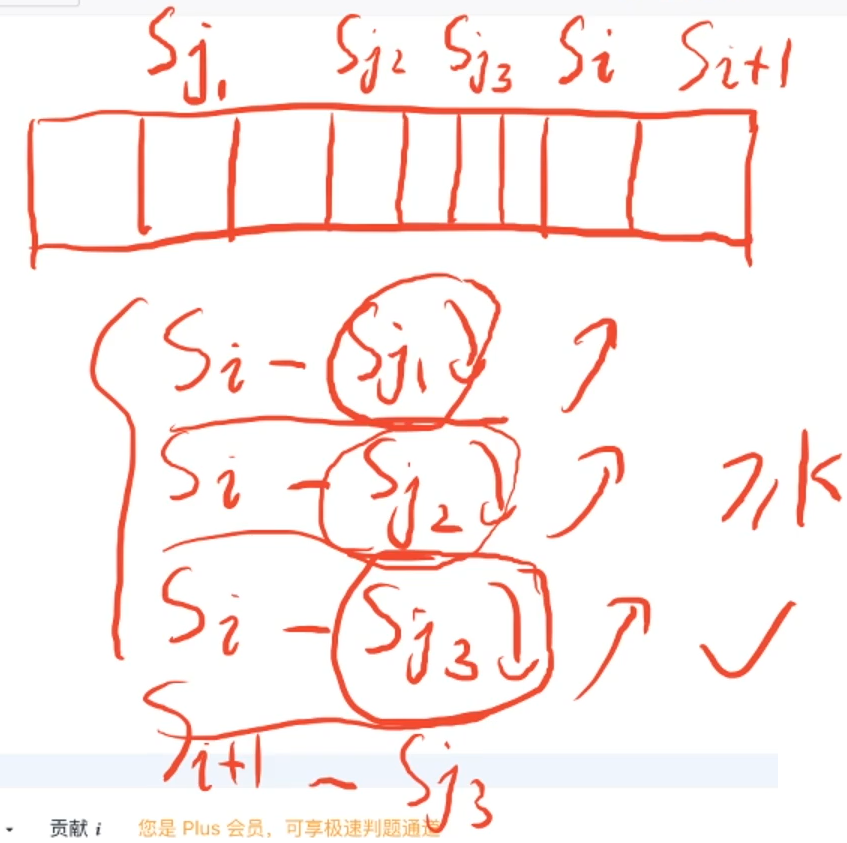
我们需要维护 S j 1 S_{j1} Sj1、 S j 2 S_{j2} Sj2 和 S j 3 S_{j3} Sj3 的单调性,本题步骤:
- 维护前缀和 S i S_i Si
- 通过前缀和得到单调递减的 S j S_j Sj 序列(这样就不用从头到尾的往后扫,直接从上一次的 S j S_j Sj 开始往后扫)
前缀和数组不单调(因为有负数),但我们单独拿出来的 S j S_j Sj 序列是单调递减的单调队列。
为什么是递减?假设 S i − S j 1 = k S_i-S_{j1} = k Si−Sj1=k,那么我们一定要保证 S j 2 S_{j2} Sj2 和 S j 3 S_{j3} Sj3 是小于 S j 1 S_{j1} Sj1 的,要不然就满足不了 S i − S j ⩾ k S_i-S_j \geqslant k Si−Sj⩾k 这个条件了。
LeetCode题解:代码实现
LeetCode1438. 绝对差不超过限制的最长连续子数组
难度:
mid我们需要拿到所有子数组的 M a x − M i n Max-Min Max−Min,判断是否小于等于 l i m i t limit limit ,所以我们需要维护两个单调队列,一个存放区间的最大值,一个存放最小值。
具体分析请配合代码注释理解。
LeetCode题解:代码实现
总结
首先我们由 R M Q RMQ RMQ 问题引出了单调队列,单调队列就是解决 R M Q RMQ RMQ 问题的一种方法,也有一些局限性(它需要固定 R M Q ( x , y ) RMQ(x,y) RMQ(x,y) 中 y y y 这一侧 进行查询)但在很多特殊情况下会有一些奇妙的作用。
正统解决 R M Q RMQ RMQ 问题通常会采用线段树、树状数组和st算法(后续会涉及到)。
单调队列使用的数据结构是 D e q u e Deque Deque 双端队列,头尾都可以进行 p u s h ( ) push() push() 和 p o p ( ) pop() pop() 操作,对于维护滑动窗口的最值还是非常好用的。
-
相关阅读:
使用代理IP进行安全高效的竞争情报收集,为企业赢得竞争优势
web前端期末大作业——餐品后台管理系统(html+css+javascript)
Java8方法引用和Lambda表达式实例源码+笔记分享
ssh密钥登录服务器
安卓应用开发——Android Studio中关于使用Androidstudio的注意事项
为什么负数存储要取反加 1 ?
线程间实现通信的几种方式
【云IDE】CSDN云IDE的初探以及实战操作
Java switch case语句详解
CDMP证书是什么样?CDMP证书有用吗?
- 原文地址:https://blog.csdn.net/weixin_53407527/article/details/126641926
