-
【论文解读系列】NER方向:LatticeLSTM (ACL2018)
简介
LatticeLSTM 出自于 ACL2018中的Chinese NER Using Lattice LSTM。
论文地址:
https://arxiv.org/abs/1805.02023有多个版本的代码:
官方版:https://github.com/jiesutd/LatticeLSTM
其他人复现版:https://github.com/LeeSureman/Batch_Parallel_LatticeLSTMLSTM-CRF模型在英文命名实体识别任务中具有显著效果,在中文NER任务中,基于字符的NER模型也明显优于基于词的NER模型(避免分词错误对NER任务的影响)。在基于字符的NER模型中引入词汇信息,确定实体边界,对中文NER任务有明显提升效果。
Lattice LSTM模型是基于词汇增强方法的中文NER的开篇之作。在该模型中,使用了字符信息和所有词序列信息,具体地,当我们通过词汇信息(词典)匹配一个句子时,可以获得一个类似Lattice的结构。这种方式可以避免因分词错误导致实体识别错误,在中文NER任务上有显著效果。
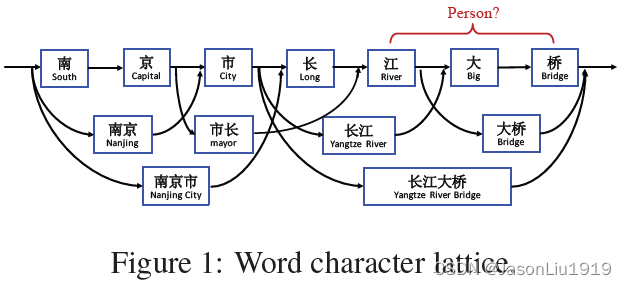
模型结构
LSTM结构
LSTM是RNN的一个变体,能够有效解决梯度消失和梯度爆炸的问题。主要引入了三个门,即输入门 i t i_t it,遗忘门 f t f_t ft,输出门 o t o_t ot 并用一个新的Cell State c t c_t ct进行信息的线性传输,同时非线性的输出信息到隐藏层的Hidden State h t h_t ht。
公式如下:
[ i t o t f t c ~ t ] = [ σ σ σ tanh ] ( W [ X t h t − 1 ] + b ) c t = f t ⊙ c t − 1 + i t ⊙ c ~ t h t = o t ⊙ tanh ( c t ) [itotft˜ct]=[σσσtanh](W[Xtht−1]+b)ct=ft⊙ct−1+it⊙˜ctht=ot⊙tanh(ct) ⎣ ⎡itotftc~t⎦ ⎤=⎣ ⎡σσσtanh⎦ ⎤(W[Xtht−1]+b)ct=ft⊙ct−1+it⊙c~tht=ot⊙tanh(ct)从上述公式可以看出:
-
输入门 i t \mathbf{i}_{t} it 用于控制当前候选状态 c ~ t \tilde{\mathbf{c}}_{t} c~t 有多少信息需要保存。
-
遗忘门 f t \mathbf{f}_{t} ft 用于控制上一个状态 c t − 1 \mathbf{c}_{t-1} ct−1 需要遗忘多少信息。
-
输出门 o t \mathbf{o}_{t} ot 用户控制当前时刻的状态 c t \mathbf{c}_{t} ct 有多少信息需要输出给 h t \mathbf{h}_{t} ht
文中介绍了3类模型方案,包括 Character-Based Model、Word-Based Model 和 Lattice Model,但是其主要网络结构都是LSTM-CRF。
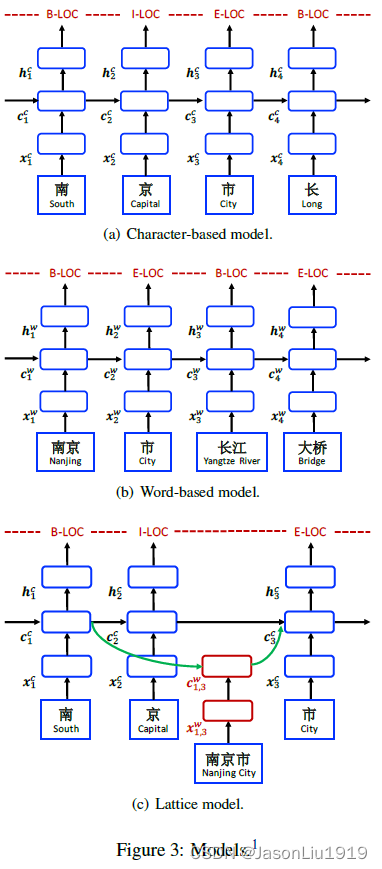
Character-Based Model
对于Character-Based模型,输入为字符序列 c 1 , c 2 , … , c m c_{1}, c_{2}, \ldots, c_{m} c1,c2,…,cm ,直接输入到LSTM-CRF。其中每个字符 c j c_{j} cj 表征为 x j c = e c ( c j ) , e c \mathbf{x}_{j}^{c}=\mathbf{e}^{c}\left(c_{j}\right) ,\mathbf{e}^{c} xjc=ec(cj),ec 是字符的嵌入矩阵,即字符表征的查找表。通常使用双向的LSTM对输入的字符表征序列 x 1 , x 2 , … , x m \mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{m} x1,x2,…,xm 进行处理,得到从左到右和从右到左 的Hidden State序列 h → 1 c , h → 2 c , … , h → m c \overrightarrow{\mathbf{h}}_{1}^{c}, \overrightarrow{\mathbf{h}}_{2}^{c}, \ldots, \overrightarrow{\mathbf{h}}_{m}^{c} h1c,h2c,…,hmc 和 h ← 1 c , h ← 2 c , … , h ← m c \overleftarrow{\mathbf{h}}_{1}^{c}, \overleftarrow{\mathbf{h}}_{2}^{c}, \ldots, \overleftarrow{\mathbf{h}}_{m}^{c} h1c,h2c,…,hmc。再将两个方向的字符表征拼接,即每个字符的Hidden State表示为: h j c = [ h → j c ; h ← j c ] \mathbf{h}_{j}^{c}=\left[\overrightarrow{\mathbf{h}}_{j}^{c} ; \overleftarrow{\mathbf{h}}_{j}^{c}\right] hjc=[hjc;hjc]
最后在 h 1 c , h 2 c , … , h m c \mathbf{h}_{1}^{c}, \mathbf{h}_{2}^{c}, \ldots, \mathbf{h}_{m}^{c} h1c,h2c,…,hmc之后接一个标准的CRF层进行序列标注。这里的上标 c c c 表示是字符级别。此外,Character-Based模型还可以融合n-gram信息(char+bichar)和分词信息(char+softword)。
- Char + bichar:直接把bigram的嵌入表示和char的嵌入表示进行拼接作为该字符的嵌入表示。
- Char + softword:分词信息可以作为soft特征加入到 Character-Based模型中。将分词标签嵌入表征和字符嵌入表征拼接
x j c = [ e c ( c j ) ; e s ( seg ( c j ) ) ] \mathbf{x}_{j}^{c}=\left[\mathbf{e}^{c}\left(c_{j}\right) ; \mathbf{e}^{s}\left(\operatorname{seg}\left(c_{j}\right)\right)\right] xjc=[ec(cj);es(seg(cj))]
其中 e s \mathbf{e}^{s} es是分词标签嵌入表示的嵌入矩阵, s e g ( c j ) seg(c_j) seg(cj)表示对于 c j c_j cj字符的分词标签结果,主要有BMES这4种标签结果,表示该字符分词结果所处的位置。
Word-Based Model
Word-Based模型与Character-Based模型类似。输入为词序列 w 1 , w 2 , . . . , w n w_1,w_2,...,w_n w1,w2,...,wn,每个词 w i w_i wi的词表征: x i w = e w ( w i ) \mathbf{x}_{i}^{w}=\mathbf{e}^{w}(w_i) xiw=ew(wi),其中 e w \mathbf{e}^{w} ew是词嵌入矩阵。同理,也是输入双向LSTM,再将两个结果拼接作为输出的Hidden State。通过 连接softmax和CRF实现序列标注。
Word-Based还可以进一步融合字符信息。词 w i w_i wi中的字符表征记为 x i c \mathbf{x}_{i}^c xic,将两者的拼接结果作为词的新表征:
x i w = [ e w ( w i ) ; x i c ] \mathbf{x}_{i}^{w}=[\mathbf{e}^{w}\left(w_{i}\right);\mathbf{x}_{i}^c] xiw=[ew(wi);xic]
至于如何获取词 w i w_i wi中的字符表征 x i c \mathbf{x}_{i}^c xic,有以下3种方式:-
Word + char LSTM:直接把每个字符输入到双向LSTM,将两个方向hidden state拼接起来作为词 w i w_i wi的字符表征:
x i c = [ h → t ( i , len ( i ) ) c ; h ← t ( i , 1 ) c ] \mathbf{x}_{i}^{c}=\left[\overrightarrow{\mathbf{h}}_{t(i, \operatorname{len}(i))}^{c} ; \overleftarrow{\mathbf{h}}_{t(i, 1)}^{c}\right] xic=[ht(i,len(i))c;ht(i,1)c]
其中 t ( i , k ) t(i,k) t(i,k)表示句子中第 i i i个词中索引为 k k k的字符,所以 t ( i , l e n ( i ) ) t(i,len(i)) t(i,len(i)) 表示词 w i w_i wi的最后一个字符。可以看出,这种方式其实只取首尾字符的拼接结果。 -
Word + char LSTM’:与上述方式不同,这种方式使用一个LSTM获得每个字符 c j c_j cj的双向表征,再拼接作为字符的hidden states表征,最后再融入到词表征中。该方式与Liu et al. (2018)的结构相似但是没有使用highway layer。
-
Word + char CNN:使用CNN抽取每个词的字符序列表征,字符表征 x i c \mathbf{x}^c_i xic,字符 c j c_j cj的词向量用 e c ( c j ) \mathbf{e}^c(c_j) ec(cj)表示:
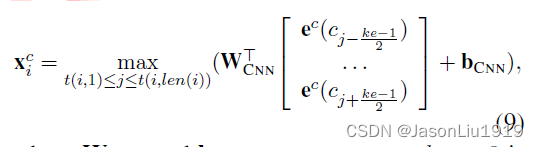
其中 W C N N \mathbf{W_{CNN}} WCNN和 b C N N \mathbf{b_{CNN}} bCNN都是待学习的参数, k e ke ke表示kernal size,文中取值为3, m a x max max表示最大池化。
Lattice Model
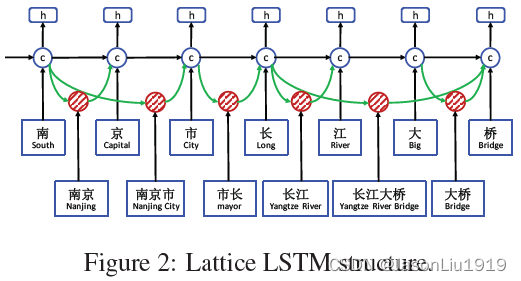
Lattice LSTM可以看做是Character-Based模型的扩展,其添加了词作为输入(比如下图输入中包括“南京市”,用红色这部分网络结构来抽取特征)和额外的门(下图的绿色线连接的门控单元)来控制信息流动。
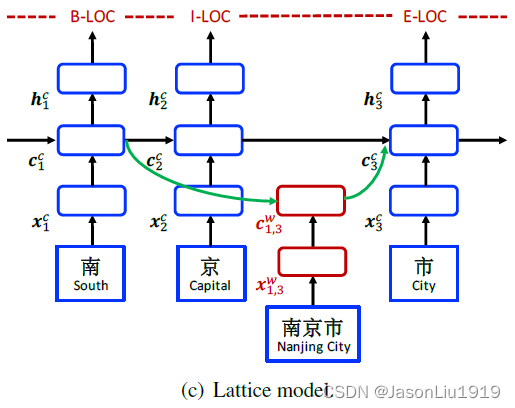
Lattice LSTM的输入为:字符序列 c 1 , c 2 , . . . , c m c_1,c_2,...,c_m c1,c2,...,cm,与词典 D D D中单词匹配的所有字符子序列记为 w b , e d w_{b,e}^d wb,ed, b b b是起始字符的下标, e e e是结束字符的下标。比如对于Figure 1中的句子"南京市长江大桥"的分词结果, w 1 , 2 d w^d_{1,2} w1,2d表示"南京"。模型的输入有4种向量:输入向量、隐藏层输出向量、cell 向量、门控向量。输入向量就是字符向量, x j c = e c ( c j ) \mathbf{x}^c_j=\mathbf{e}^c(c_j) xjc=ec(cj)。LSTM模型的递归结构体现于每个字符 c j c_j cj上使用一个字符cell向量 c j c \mathbf{c}^c_j cjc和一个隐藏层向量 h j c \mathbf{h}^c_j hjc,其中 c j c \mathbf{c}^c_j cjc用来记录从句子开始到字符 c j c_j cj的信息流动,最终将 h j c \mathbf{h}_j^c hjc输入到CRF层进行序列标注。
与character-based模型不同,计算 c j c \mathbf{c}^c_j cjc时要考虑句子中对应词典的子串 w b , e d w^d_{b,e} wb,ed,每个子串串 w b , e d w^d_{b,e} wb,ed的表征为: x b , e w = e w ( w b , e d ) \mathbf{x}^w_{b,e}=\mathbf{e}^w(w^d_{b,e}) xb,ew=ew(wb,ed)。此外,词的cell State c b , e w \mathbf{c}^w_{b,e} cb,ew表示从句子开始的递归状态 x b , e w \mathbf{x}^w_{b,e} xb,ew,计算如下:
[ i b , e w f b , e w c ~ b , e w ] = [ σ σ tanh ] ( W w ⊤ [ x b , e w h b c ] + b w ) c b , e w = f b , e w ⊙ c b c + i b , e w ⊙ c ~ b , e w [iwb,efwb,e˜cwb,e]=[σσtanh](Ww⊤[xwb,ehcb]+bw)cwb,e=fwb,e⊙ccb+iwb,e⊙˜cwb,e ⎣ ⎡ib,ewfb,ewc b,ew⎦ ⎤cb,ew=⎣ ⎡σσtanh⎦ ⎤(Ww⊤[xb,ewhbc]+bw)=fb,ew⊙cbc+ib,ew⊙c b,ew
其中, i b , e w \mathbf{i}_{b, e}^w ib,ew和 f b , e w \mathbf{f}_{b, e}^w fb,ew分别是输入门和遗忘门。 h b c \mathbf{h}_b^c hbc和 c b c \mathbf{c}_b^c cbc分别是来自词的 首字 LSTM单元输出的Hidden State和Cell State,比如计算词长江大桥的cell state, h b c \mathbf{h}_b^c hbc和 c b c \mathbf{c}_b^c cbc来自于长字,而计算大桥的cell State, h b c \mathbf{h}_b^c hbc和 c b c \mathbf{c}_b^c cbc来自于大字。此外需要注意的是,对于word级别的cell没有output gate,这是因为序列标注的标注结果都在character级别上。通过词的 cell status c b , e w \mathbf{c}^w_{b,e} cb,ew会有更多的递归路径信息流进每个 c j c \mathbf{c}^c_j cjc。例如Figure 2中,输入源 c 7 c \mathbf{c}^c_7 c7c包括 x 7 c \mathbf{x}^c_7 x7c(桥)、 c 6 , 7 w \mathbf{c}^w_{6,7} c6,7w(大桥)、 c 4 , 7 w \mathbf{c}^w_{4,7} c4,7w(长江大桥)。将所有的 c b , e w \mathbf{c}^w_{b,e} cb,ew链接到cell c e c \mathbf{c}^c_e cec,即对这3部分信息进行加权相加。对每个子串的cell status c b , e w \mathbf{c}^w_{b,e} cb,ew使用一个额外的门 i b , e c \mathbf{i}^c_{b,e} ib,ec来控制流进 c e c \mathbf{c}^c_e cec的信息流(原文是 c b , e c \mathbf{c}^c_{b,e} cb,ec,应该是写错了):
计算字符 c j c c_j^c cjc的cell state c j c \mathbf{c}_j^c cjc,即对所有以 c j c c_j^c cjc结尾的词的cell state和 c j c c_j^c cjc的候选状态 c ~ j c \widetilde{\boldsymbol{c}}_j^c c jc进行加权相加。因此字符 c j c c_j^c cjc的cell status c j c \mathbf{c}_j^c cjc 的计算如下:
c j c = ∑ b ∈ { b ′ ∣ w b ′ , j d ∈ D } α b , j c ⊙ c b , j w + α j c ⊙ c ~ j c \mathbf{c}_j^c=\sum_{b \in\left\{b^{\prime} \mid w_{b^{\prime}, j}^d \in \mathbb{D}\right\}} \boldsymbol{\alpha}_{b, j}^c \odot \boldsymbol{c}_{b, j}^w+\boldsymbol{\alpha}_j^c \odot \widetilde{\boldsymbol{c}}_j^c cjc=b∈{b′∣wb′,jd∈D}∑αb,jc⊙cb,jw+αjc⊙c jc上述式子中的 α \alpha α是门控归一化结果,门控根据当前词的cell state c b , e w \mathbf{c}_{b, e}^w cb,ew和字符嵌入 x e c \mathbf{x}_{e}^c xec计算如下:
i b , e c = σ ( W l ⊤ [ x e c c b , e w ] + b l ) \mathbf{i}_{b, e}^c=\sigma\left(\mathbf{W}^{l \top}\left[xcecwb,e\right]+\mathbf{b}^l\right) ib,ec=σ(Wl⊤[xeccb,ew]+bl)i b , j c \mathbf{i}_{b, j}^c ib,jc 和 i j c \mathbf{i}_j^c ijc分别归一化为 α b , j c \boldsymbol{\alpha}_{b, j}^c αb,jc 和 α j c \boldsymbol{\alpha}_j^c αjc,使其求和为 1 \mathbf{1} 1:
α b , j c = exp ( i b , j c ) exp ( i j c ) + ∑ b ′ ∈ { b ′ ′ ∣ w b ′ ′ , j d ∈ D } exp ( i b ′ , j c ) α j c = exp ( i j c ) exp ( i j c ) + ∑ b ′ ∈ { b ′ ′ ∣ w b ′ ′ , j d ∈ D } exp ( i b ′ , j c ) αcb,j=exp(icb,j)exp(icj)+∑b′∈{b′′∣wdb′′,j∈D}exp(icb′,j)αcj=exp(icj)exp(icj)+∑b′∈{b′′∣wdb′′,j∈D}exp(icb′,j) αb,jcαjc=exp(ijc)+∑b′∈{b′′∣wb′′,jd∈D}exp(ib′,jc)exp(ib,jc)=exp(ijc)+∑b′∈{b′′∣wb′′,jd∈D}exp(ib′,jc)exp(ijc)
以
南京市长江大桥为例,计算桥的cell state,是通过对长江大桥,大桥的cell state,以及桥的候选cell state,进行加权求和。加权系数,则是对字符和词的门控进行Softmax得到。
需要指出的是,当前字符有词汇融入时,则采取上述公式进行计算;如当前字符没有词汇时,则采取原生的LSTM进行计算。换句话说,当有词汇信息时,Lattice LSTM并没有利用前一时刻的记忆向量 c j − 1 c c_{j-1}^c cj−1c,即不保留对词汇信息的持续记忆。Decoding 和 Training
Decoding 部分,就是在 h 1 , h 2 , . . . , h τ \mathbf{h}_{1},\mathbf{h}_{2},...,\mathbf{h}_{\tau} h1,h2,...,hτ之后接一个CRF层计算输出概率,然后选择最大的输出概率argmaxP(y|s)。对于Character-Based Model, τ \tau τ值为 n n n,对于Word-Based Model, τ \tau τ值为 m m m。下面是计算某个标注序列 y y y的概率。
P ( y ∣ s ) = exp ( ∑ i ( W C R F l i h i + b C R F ( l i − 1 , l i ) ) ) ∑ y ′ exp ( ∑ i ( W C R F l i ′ h i + b C R F ( l i − 1 ′ , l i ′ ) ) ) P(y \mid s)=\frac{\exp \left(\sum_{i}\left(\mathbf{W}_{\mathrm{CRF}}^{l_{i}} \mathbf{h}_{i}+b_{\mathrm{CRF}}^{\left(l_{i-1}, l_{i}\right)}\right)\right)}{\sum_{y^{\prime}} \exp \left(\sum_{i}\left(\mathbf{W}_{\mathrm{CRF}}^{l_{i}^{\prime}} \mathbf{h}_{i}+b_{\mathrm{CRF}}^{\left(l_{i-1}^{\prime}, l_{i}^{\prime}\right)}\right)\right)} P(y∣s)=∑y′exp(∑i(WCRFli′hi+bCRF(li−1′,li′)))exp(∑i(WCRFlihi+bCRF(li−1,li)))
使用一阶Viterbi算法找到得分最高的标注序列,损失函数是带L2正则的log-likelihood loss。
L = ∑ i = 1 N log ( P ( y i ∣ s i ) ) + λ 2 ∥ Θ ∥ 2 L=\sum_{i=1}^{N} \log \left(P\left(y_{i} \mid s_{i}\right)\right)+\frac{\lambda}{2}\|\Theta\|^{2} L=i=1∑Nlog(P(yi∣si))+2λ∥Θ∥2
缺点:
- 计算性能低下,不能batch并行化。究其原因主要是每个字符之间的增加word cell(看作节点)数目不一致;
- 信息损失:1)每个字符只能获取以它为结尾的词汇信息,对于其之前的词汇信息也没有持续记忆。如对于「药」,并无法获得‘inside’的「人和药店」信息。2)由于RNN特性,采取BiLSTM时其前向和后向的词汇信息不能共享。
- 可迁移性差:只适配于LSTM,不具备向其他网络迁移的特性
-
-
相关阅读:
C#中的(++)和(--)运算符
R语言将列表数据转化为向量数据(使用unlist函数将列表数据转化为向量数据)
Redis哨兵机制原理
java基础---01
密码学 数字签名
Java.lang.Class类 getResource()方法有什么功能呢?
面试题四:请解释一下watch,computed和filter之间的区别
Jira 笔记
如何让AI生成自己喜欢的歌曲-AI音乐创作的正确方式 - 第507篇
关于python内置数据类型的小练习
- 原文地址:https://blog.csdn.net/ljp1919/article/details/126657649