一种曲线递增策略的自适应粒子群算法研究-附代码

一种曲线递增策略的自适应粒子群算法研究

摘要：群智能算法以其动态寻优能力强、实现途径简单等特点不断成为进化算法领域的研究热点。控参的选择对算法寻优性能有着极大影响,首先从数学推导角度对粒子群参数进行深入研究,接着提出一种契合粒子本身进化公式的,且具有反向思维的曲线递增策略的改进算法。最后验证该算法具备以下两点突出优势:a)有效避免早熟问题,在处理维度灾难问题上,寻优性能更强,且具备良好的平衡全局与局部寻优性能; b)算法控参简单,可有效解决鲁棒性低且繁琐的人工调参问题。

1.粒子群优化算法

基础粒子群算法的具体原理参考网络资料

2. 改进粒子群算法

2.1 曲线递增策略

曲线递增(curves increasing)是本文提出的一种基于指数函数图像的控参策略。给定惯性权值 $w_{max}$,曲线递增公式如下：
$$\begin{array}{c}{w}_1=w_{\max }-\frac{w_{\max }}{T_{\max }}\cdot t_{(\text{time })}\\ w=e^{-w_1}\end{array}$$
其中, $w_{\text{max }}$ 为设定的较大惯性权值 $\left(w_{\text{max }}\ge 1\right),t_{(time)}$ 为当前迭代 的次数, 最大迭代次数为 $T_{\max }$; 随着迭代次数增加, ${\mathrm{w}}_1$ 逐渐 减少, $\mathrm{w}$ 逐渐增大。运用上述自适应权值变化公式, 粒子在 前期因权值较小, 具备精细搜索能力, 结合图像可知, 算法 迭代前期 $w_1$ 值在较大范围内的缩减趋势极其缓慢, 保证了粒 子局部搜索的充分性, 后期变化趋势逐渐增大, 对若干局部 解造成一定的扰动效果, 保证了对全局搜索的能力。 ${\mathrm{w}}_{\max }$ 值后期的趋势变化, 其目的不再是常规意义上的确保加快收敛, 变动趋势实际上是相对陡峭，绝对平滑。

在学习因子部分，本文提出一种改进的二阶震荡法，即引入双种群配合提出的曲线递增策略，提高群体的多样性，从而进一步改善算法的全局搜索能力。改进后的公式如下：
$$\begin{array}{c}{v}_{ij}(t)=e^{-\left(w_{\max }-\frac{w_{\max }}{T_{\max }}\ast t\right)}\ast v_{ij}(t)+{\varphi }_1\ast \left[p_{ij}(t)-\left(1+{\mu }_1\right)x_{ij}(t)+{\mu }_1{x}_{ij}^{\ast }(t)\right]+\\ {\varphi }_2\ast \left[p_{gi}(t)-\left(1+{\mu }_2\right)x_{ij}(t)+{\mu }_2{x}_{ij}^{\ast }(t)\right]\\ x_{ij}^{\ast }(t)=x_{ij}(t)\\ x_{ij}(t)=x_{ij}(t)+v_{ij}(t)\end{array}$$
其中, $x_{ij}^{\ast }$ 为新种群, 二阶震荡因子 ${\mu }_{1.2}$ 的公式为:
$${\mu }_1=\{\begin{array}{ccc}\left(2\sqrt{c_1\ast \mathrm{rand}()}-1\right)\ast \mathrm{rand}()/c_1\ast \mathrm{rand}()& w<\frac{2}{3}{w}_{\max }& (9)\\ \left(2\sqrt{c_1\ast \mathrm{rand}()}-1\right)\ast (1+\mathrm{rand}())/c_1\ast \mathrm{rand}()& w\ge \frac{2}{3}{w}_{\max }& (10)\end{array}$$
其中, $c_1、c_2$ 是人为设定的学习因子, $\mathrm{rand}()$ 为 0-1 之间随机 数, $t$ 为当前迭代次数, ${\mathrm{T}}_{\max }$ 为迭代最大次数, 改进后的粒子群算法流程如下图所示。

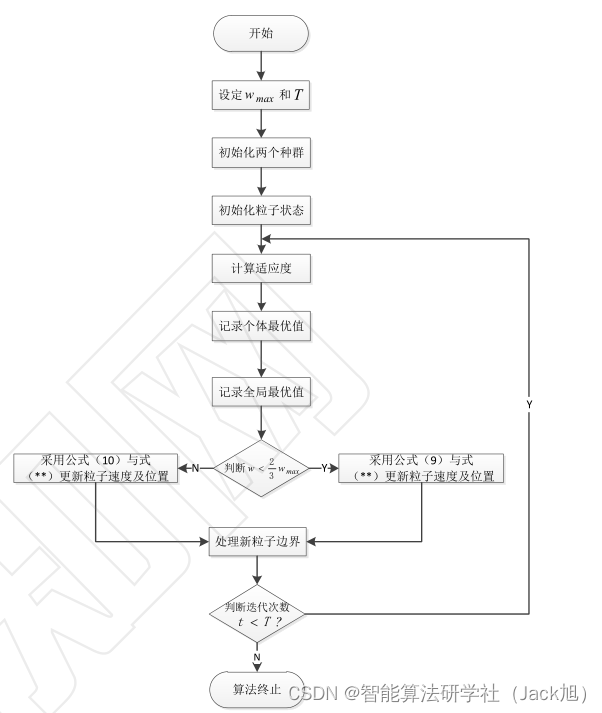
3.实验结果

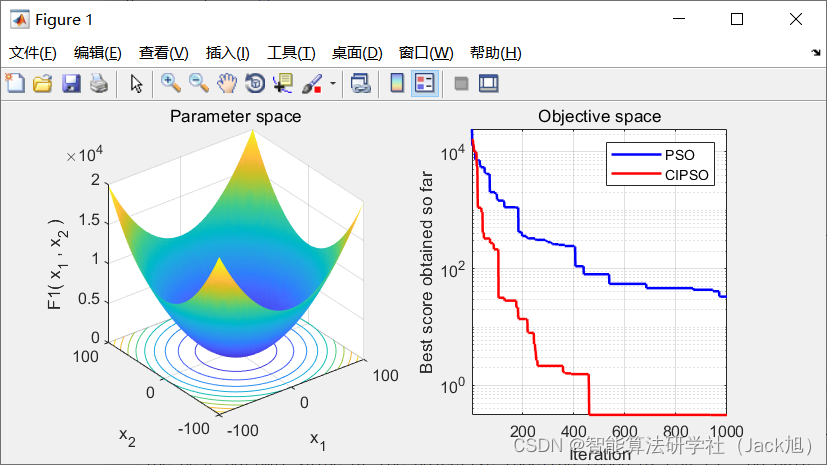
4.参考文献

[1]吴凡,洪思,杨冰,胡贤夫.曲线递增策略的自适应粒子群算法研究[J].计算机应用研究,2021,38(06):1653-1656+1661.

5.Matlab代码

6.Python代码