信息论学习笔记(一):认识通信系统

前言

最近在研究压缩算法, 不得不来学习信息论相关知识。学习信息论要看什么教程好? 当然是信息论之父香农发布的论文A Mathematical Theory of Communication(通信中的数学理论)啦!

首先声明一下, 本人英语并不是很好, 当中可能有理解错误的地方，希望大佬们指出!

步入正题: 如何处理不确定性?

正如论文标题: 什么是通信?
香农大佬给出了定义:
The fundamental problem of communication is that of reproducing at one point either exactly or approximately a message selected at another point.
实现通信最基本的问题就是在一个地方出现另一个地方的信息, 通信的信息都有特定的含义, 于是香农就抛出了问题:
The system must be designed to operate for each
possible selection, not just the one which will actually be chosen since this is unknown at the time of design.
以我的理解，大概意思是通信系统应该能处理不同情况的信息, 而不仅仅是特定的信息, 因为在实际情况下, 在实际通信系统时我们不知道会选择哪条信息。也就是随机的.

如何度量信息量?

香农大佬认为选择对数函数作为度量函数, 还介绍了它的优点。使人不得不信服, 为什么不选择一些正比例函数如线性函数(y = kx + b)度量信息量呢？毕竟它们都是与可能性成正相关的。可能是因为如果使用线性函数的话在可能状态多的时候会使得信息量非常大,而使用对数函数这相反(x -> +oo时, 导数-> 0), 纯属个人猜想, 不过还是得先跟香农大佬来。。。

比特

If the
base 2 is used the resulting units may be called binary digits, or more briefly bits
当底数为2时, 就可以得到一个二进制数位, 称之为bit(比特)
如果要记录一个电路的开关状态, 用0表示关，1表示开，那么我们只需要log(2, 2)也就是一个比特就能保存这个电路所有可能值,

同理, 如果底数为10, 我们仅仅用1个单位就能存放10种情况.
那么这样的话, 经过换算, 一个十进制数位大概为3.32比特.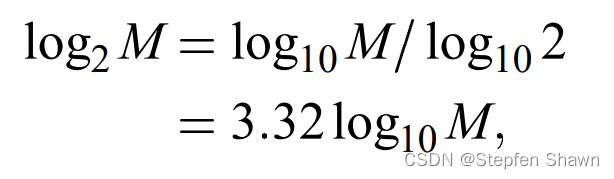

于是, 想知道可能状态N需要多少bit保存, 有一个很简单的公式:

通信系统

接下来香农展示了他眼中的通信系统

首先是信号源(INFORMATION SOURCE): 负责生成消息序列.
然后是发送器(transmitter): 对消息进行处理
接收器(receiver): ordinarily performs the inverse operation of that done by the transmitter, reconstructing the message from the signal(发送器的逆操作不就是接收吗?)
信宿(destination): 接受信号的地方

We may roughly classify communication systems into three main categories: discrete,
continuous and mixed.

香农将通信系统分为三大类:

• 离散系统: 消息和信号都是离散符合序列, 就像电报用着一系列点等符号
• 连续系统: 消息和信号都能看成连续函数(无线广播, 电视), 什么是连续函数(continuous functions)?个人理解应该是像三角, 变换这些连续的玩意吧。。。
• 混合系统: 离散和连续变量都可能出现的系统(语音传送), 也就是上面2个的结合

We first consider the discrete case. This case has applications not only in communication theory, but
also in the theory of computing machines, the design of telephone exchanges and other fields.

于是大佬就开始讨论离散部分的理论, 指出了这是适用于计算机领域理论。啃了这么久才发现刚刚开始.

离散无噪声系统

离散通道就是从一点向另一点传送选择序列(a sequence of choices), 该序列是由S1, ..., Sn组成的有限集合, 像电报这种系统就是用离散通道传递的。

下面一个离散通道的容量C定义:

至于这为什么定义的话, 明天再记录吧! 已经夜深人静了肝不动啦！！！

最后附上该论文的地址: https://people.math.harvard.edu/~ctm/home/text/others/shannon/entropy/entropy.pdf

原来日常生活中通信技术中蕴含着这么多数学原理, 到现在为止感觉我连一点皮毛都没学到。。。这是太奇妙啦!

喜欢的话给个关注吧!