【手写算法实现】 之 朴素贝叶斯 Naive Bayes 篇

【手写算法实现】 之 朴素贝叶斯 Naive Bayes 篇

朴素贝叶斯模型(naive bayes)属于分类模型，也是最为简单的概率图模型，对于之后理解HMM、CRF等模型，大有裨益。这里手写算法介绍一下朴素贝叶斯模型。

朴素贝叶斯模型

朴素贝叶斯模型（Naive Bayes）中的“朴素”就在于它的条件独立性假设：
$$p(X_1,X_2,...,X_n\mid Y)=p(X_1\mid Y)\cdot p(X_2\mid Y)\cdots p(X_n\mid Y)$$
用概率图表示如下：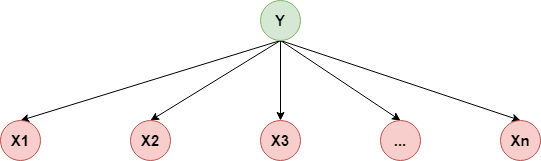

所以它的联合概率分布：
$$p(X_1,X_2,...,X_n,Y)=p(Y)\prod _{i=1}^{n}p(X_i\mid Y)$$
这里 $c_k(k=1,2,...,K)$ 表示分类器所属的类别

这里还要补充一个前提条件，就是贝叶斯定理
$$P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)}.$$
其中，P$(Y)$叫做先验概率，叫做条件概率，$P(Y|X)$叫做后验概率。

根据上面两大前提条件，我们可以得到朴素贝叶斯模型。实际上我们就是要最大化后验概率，从而得到类别标签。
$$P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{P(X=x)}=\frac{P(Y=c_k){\prod }_{j=1}^{n}P(X=x^{(i)}|Y=c_k)}{P(X=x)}$$
由于$P(X=x)$对于所有的类别标签来说的话，都是一样的，所以可以去掉，最终得到的公式如下:
$$y=argma{x}_{c_k}P(Y=c_k)\prod _{j=1}^{n}P(X=x^{(i)}|Y=c_k)$$
这就是朴素贝叶斯的公式

在朴素贝叶斯估计中，条件独立性假设是非常强的假设，实际上是为了简化运算，实际上很多时候，特征之间是存在联系的，但是这样朴素贝叶斯也更加简单，与此同时，损失了一些精度。

参数估计 先验概率与条件概率的计算

当得到了朴素贝叶斯的公式后，那么其中的$p(Y=c_k)$与$p(X_i=x_i\mid Y=c_k)$怎么求呢？在这里，我们需要分情况讨论：得看特征本身是离散的还是连续的。

• 当特征是离散的时候，我们使用极大似然估计，叫做多项式模型，MultinomialNB就是先验为多项式分布的朴素贝叶斯
• 当特征是连续的时候，我们让其满足高斯分布，叫做高斯模型，所以GaussianNB就是先验为高斯分布的朴素贝叶斯
• 当特征是二元离散值或者很稀疏的多元离散值的时候，叫做伯努利模型，BernoulliNB就是先验为伯努利分布的朴素贝叶斯。

朴素贝叶斯将实例分到后验概率最大的类中，这其实等价于经验风险最小化

多项式模型

当特征是离散的时候，我们使用极大似然估计去得到先验概率与条件概率。

1.求解 $p(Y=c_k)$
$$p(Y=c_k)=\frac{{\sum }_{i=1}^{N}I(y_i=c_k)}{N},k=1,2,...,K,N表示样本量$$
2.求解 $p(X_i=x_i\mid Y=c_k)$

假设第$i$个特征可能的取值为 A i = { a i 1 , a i 2 , . . . , a i S i } A_i=\{a_{i1},a_{i2},...,a_{iS_i}\} Ai​={ai1​,ai2​,...,aiSi​​}，所以有$x_i=a_{il}\in A_i$，所以
$$p(X_i=x_i\mid Y=c_k)=p(X_i=a_{il}\mid Y=c_k)=\frac{{\sum }_{j=1}^{N}I(x_i^j=a_{il},y_i=c_k)}{{\sum }_{i=1}^{n}I(y_j=c_k)}$$
但是，在计算先验概率与条件概率的时候，我们会做一些平滑处理，以防出现为0的情况，从而影响到后验概率的计算。这种操作叫做laplace平滑 拉普拉斯平滑，这一部分就是采用贝叶斯估计
$$P_{\lambda }\left(X^{(j)}=a_{jl}\mid Y=c_k\right)=\frac{{\sum }_{i=1}^{N}I\left(x_i^{(j)}=a_{jl},y_i=c_k\right)+\lambda }{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)+S_j\lambda }$$
式中 $\lambda ⩾0$. 等价于在随机变量各个取值的频数上赋予一个正数 $\lambda >0$. 当 $\lambda =0$ 时 就是极大似然估计. 常取 $\lambda =1$, 这时称为拉普拉斯平滑 (Laplace smoothing). 显 然, 对任何 $l=1,2,\cdots ,S_j,k=1,2,\cdots ,K$, 有
$$\begin{array}{l}{P}_{\lambda }\left(X^{(j)}=a_{jl}\mid Y=c_k\right)>0\\ {\sum }_{l=1}^{s_j}P\left(X^{(j)}=a_{jl}\mid Y=c_k\right)=1\end{array}$$
同样，先验概率的贝叶斯估计是
$$P_{\lambda }\left(Y=c_k\right)=\frac{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)+\lambda }{N+K\lambda }$$

高斯模型

特征为连续值的时候，我们就不能采取多项式模型来估计先验概率与条件概率了，因为会导致很多 $P(X=x_i|Y=c_k)$ 等于0。所以需要采用高斯模型。高斯模型的思想是：让特征的每一维都满足高斯分布(正态分布)，从而来处理连续特征。注意，先验概率的计算与多项式模型相同。公式如下：
$$P(X^{(j)}=a|Y=c_k)=\frac{1}{\sqrt{2\pi {\sigma }_{c_k,j}^2}}exp(-\frac{(a-{\mu }_{c_k,j}{)}^2}{2{\sigma }_{c_k,j}^2})$$
其中， ${\sigma }_{c_k,j}^2$ 表示类别是 $c_k$ 的实例中，第 $j$ 维特征的方差， ${\mu }_{c_k,j}$ 表示类别是 $c_k$ 的实例中，第 $j$ 维特征的均值

当求出先验概率与条件概率之后，再带入到朴素贝叶斯公式中，就可以得到实例的类别标签了。

朴素贝叶斯模型的python实现

只有把模型实现一遍才说明是真的掌握了，这里用了两种方法实现，一个是纯python实现，以及调用scikit-learn库来实现。

########-----NaiveBayes------#########
class NaiveBayes():
    def __init__(self) -> None:
        self.y = None
        self.classes = None
        self.classes_num = None # 类别数量
        self.parameters = []
        
    def fit(self, X, y) -> None:
        self.y = y
        self.classes = np.unique(y) # 类别 
        self.classes_num = len(self.classes) 
        # 计算每个特征针对每个类的均值和方差
        for i, c in enumerate(self.classes):
            # 选择类别为c的X
            X_where_c = X[np.where(self.y == c)]
            self.parameters.append([])
            # 添加均值与方差
            for col in X_where_c.T:
                parameters = {"mean": col.mean(), "var": col.var()}
                self.parameters[i].append(parameters)
    
    def _calculate_prior(self, c):
        '''
        先验函数，也就是求先验概率
        利用极大似然估计的结果得到
        '''
        frequency = np.mean(self.y == c)
        return frequency
        # 贝叶斯估计的先验概率
        frequency = (np.sum(self.y == c) + 1) / (len(X) + self.classes_num)
        
    def _calculate_likelihood(self, mean, var, X): 
        """
        似然函数
        """
        # 高斯概率
        eps = 1e-4 # 防止除数为0
        coeff = 1.0 / math.sqrt(2.0 * math.pi * var + eps)
        exponent = math.exp(-(math.pow(X - mean, 2) / (2 * var + eps)))
        return coeff * exponent
    
    
    def _calculate_probabilities(self, X):
        posteriors = [] # 后验概率
        for i,c in enumerate(self.classes):
            # p(y)
            posterior = self._calculate_prior(c)
            # p(x | y)
            for feature_value, params in zip(X, self.parameters[i]):
                # 独立性假设
                # P(x1,x2|Y) = P(x1|Y)*P(x2|Y)
                likelihood = self._calculate_likelihood(params["mean"], params["var"], feature_value)
                posterior *= likelihood
            posteriors.append(posterior)
        # 返回具有最大后验概率的类别
        return self.classes[np.argmax(posteriors)]
            
    def predict(self, X):
        y_pred = [self._calculate_probabilities(sample) for sample in X]
        return y_pred
    
    def score(self, X, y):
        y_pred = self.predict(X)
        accuracy = np.sum(y == y_pred, axis=0) / len(y)
        return accuracy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

iris数据集测试

def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, :])
    return data[:,:-1], data[:,-1]
1
2
3
4
5
6
7

用自定义 NaiveBayes 模型

# 用自定义 NaiveBayes 模型
model = NaiveBayes()
model.fit(X_train, y_train)
# 测试数据
print(model.score(X_test, y_test))
1
2
3
4
5

1.0
1

从sklearn 包中调用GaussianNB 测试

# 从sklearn 包中调用GaussianNB 测试
from sklearn.naive_bayes import GaussianNB
skl_model = GaussianNB()
# 训练数据集
skl_model.fit(X_train, y_train)
# 测试数据
print(skl_model.score(X_test, y_test))
1
2
3
4
5
6
7

1.0
1

完整代码

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
import math

########-----NaiveBayes------#########
class NaiveBayes():
    def __init__(self) -> None:
        self.y = None
        self.classes = None
        self.classes_num = None # 类别数量
        self.parameters = []
        
    def fit(self, X, y) -> None:
        self.y = y
        self.classes = np.unique(y) # 类别 
        self.classes_num = len(self.classes) 
        # 计算每个特征针对每个类的均值和方差
        for i, c in enumerate(self.classes):
            # 选择类别为c的X
            X_where_c = X[np.where(self.y == c)]
            self.parameters.append([])
            # 添加均值与方差
            for col in X_where_c.T:
                parameters = {"mean": col.mean(), "var": col.var()}
                self.parameters[i].append(parameters)
    
    def _calculate_prior(self, c):
        '''
        先验函数，也就是求先验概率
        利用极大似然估计的结果得到
        '''
        frequency = np.mean(self.y == c)
        return frequency
        # 贝叶斯估计的先验概率
        frequency = (np.sum(self.y == c) + 1) / (len(X) + self.classes_num)
        
    def _calculate_likelihood(self, mean, var, X): 
        """
        似然函数
        """
        # 高斯概率
        eps = 1e-4 # 防止除数为0
        coeff = 1.0 / math.sqrt(2.0 * math.pi * var + eps)
        exponent = math.exp(-(math.pow(X - mean, 2) / (2 * var + eps)))
        return coeff * exponent
    
    
    def _calculate_probabilities(self, X):
        posteriors = [] # 后验概率
        for i,c in enumerate(self.classes):
            # p(y)
            posterior = self._calculate_prior(c)
            # p(x | y)
            for feature_value, params in zip(X, self.parameters[i]):
                # 独立性假设
                # P(x1,x2|Y) = P(x1|Y)*P(x2|Y)
                likelihood = self._calculate_likelihood(params["mean"], params["var"], feature_value)
                posterior *= likelihood
            posteriors.append(posterior)
        # 返回具有最大后验概率的类别
        return self.classes[np.argmax(posteriors)]
            
    def predict(self, X):
        y_pred = [self._calculate_probabilities(sample) for sample in X]
        return y_pred
    
    def score(self, X, y):
        y_pred = self.predict(X)
        accuracy = np.sum(y == y_pred, axis=0) / len(y)
        return accuracy
    
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, :])
    return data[:,:-1], data[:,-1]

if __name__ == '__main__':
    # iris 数据集测试
    X, y = create_data()
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
    print(X_train[0], y_train[0])
    
    # 用自定义 NaiveBayes 模型
    model = NaiveBayes()
    model.fit(X_train, y_train)
    # 测试数据
    print(model.score(X_test, y_test))
    
    # 从sklearn 包中调用GaussianNB 测试
    from sklearn.naive_bayes import GaussianNB
    skl_model = GaussianNB()
    # 训练数据集
    skl_model.fit(X_train, y_train)
    # 测试数据
    print(skl_model.score(X_test, y_test))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100