-
图问题——深度遍历,广度遍历,并查集
一般而言,如果一个问题是关于事物状态的改变,那么可以考虑把该问题转化为图的搜索问题。
剑指 Offer II 108. 单词演变
在字典(单词列表) wordList 中,从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
序列中第一个单词是 beginWord 。
序列中最后一个单词是 endWord 。
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典 wordList 中的单词。
给定两个长度相同但内容不同的单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。输入:beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出:5
解释:一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的长度 5。意思是从开始到结尾,每个单词之间只能改变一个字母
广度优先算法可以计算路径的长度或者最短路径,像树一样,层序遍历求有多少层,到每层时先计算这一层的元素有多少。但并不是真的构造一个树,也没有边相连,在寻找子节点时用下面的方法。

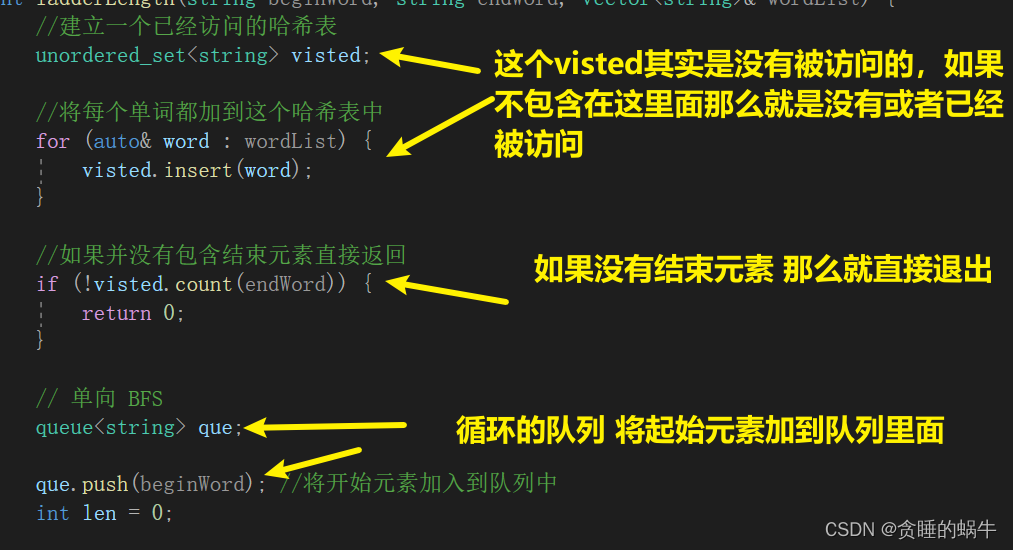
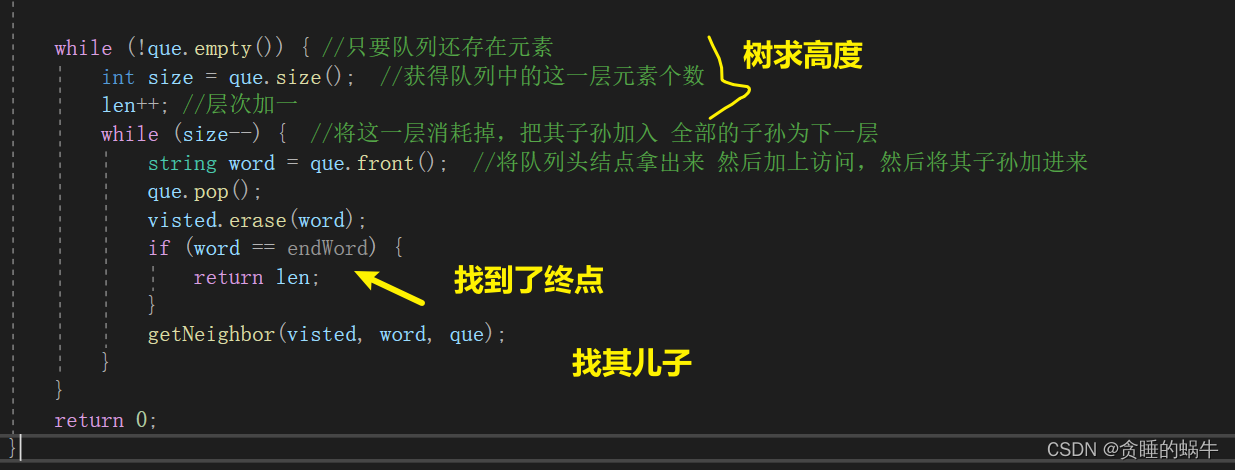
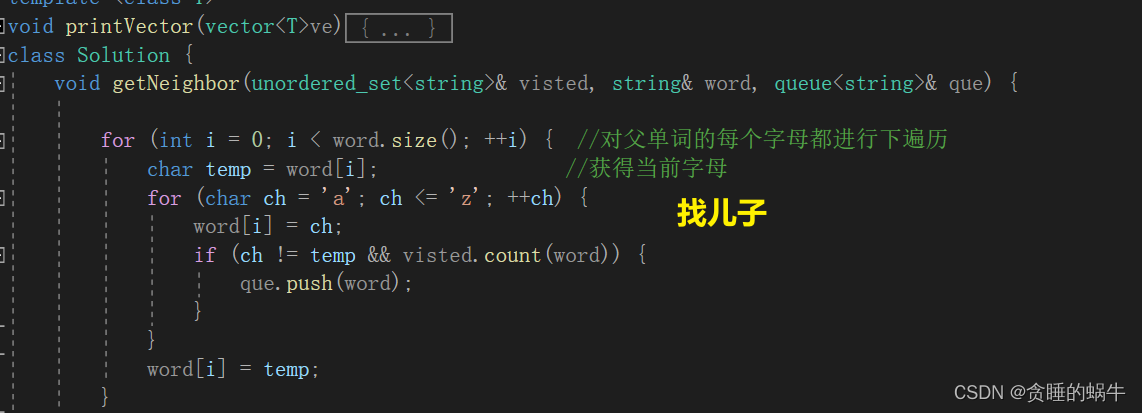
class Solution { void getNeighbor(unordered_set<string>& visted, string& word, queue<string>& que) { for (int i = 0; i < word.size(); ++i) { //对父单词的每个字母都进行下遍历 char temp = word[i]; //获得当前字母 for (char ch = 'a'; ch <= 'z'; ++ch) { word[i] = ch; if (ch != temp && visted.count(word)) { que.push(word); } } word[i] = temp; } } public: int ladderLength(string beginWord, string endWord, vector<string>& wordList) { //建立一个已经访问的哈希表 unordered_set<string> visted; //将每个单词都加到这个哈希表中 for (auto& word : wordList) { visted.insert(word); } //如果并没有包含结束元素直接返回 if (!visted.count(endWord)) { return 0; } // 单向 BFS queue<string> que; que.push(beginWord); //将开始元素加入到队列中 int len = 0; while (!que.empty()) { //只要队列还存在元素 int size = que.size(); //获得队列中的这一层元素个数 len++; //层次加一 while (size--) { //将这一层消耗掉,把其子孙加入 全部的子孙为下一层 string word = que.front(); //将队列头结点拿出来 然后加上访问,然后将其子孙加进来 que.pop(); visted.erase(word); if (word == endWord) { return len; } getNeighbor(visted, word, que); } } return 0; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
剑指 Offer II 109. 开密码锁
一个密码锁由 4 个环形拨轮组成,每个拨轮都有 10 个数字: ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。每个拨轮可以自由旋转:例如把 ‘9’ 变为 ‘0’,‘0’ 变为 ‘9’ 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 ‘0000’ ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,请给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。

和上题一个思路剑指 Offer II 110. 所有路径(有向图 深度遍历)
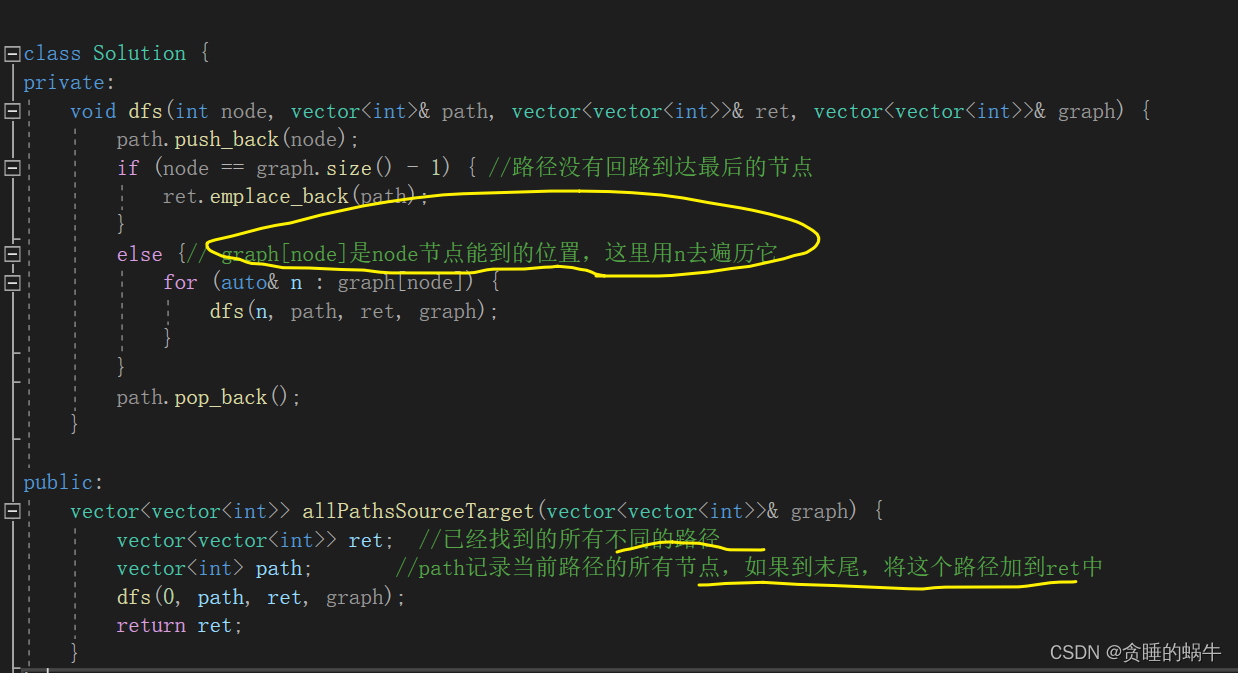
给定一个有 n 个节点的有向无环图,用二维数组 graph 表示,请找到所有从 0 到 n-1 的路径并输出(不要求按顺序)。
graph 的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些结点(译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a ),若为空,就是没有下一个节点了。
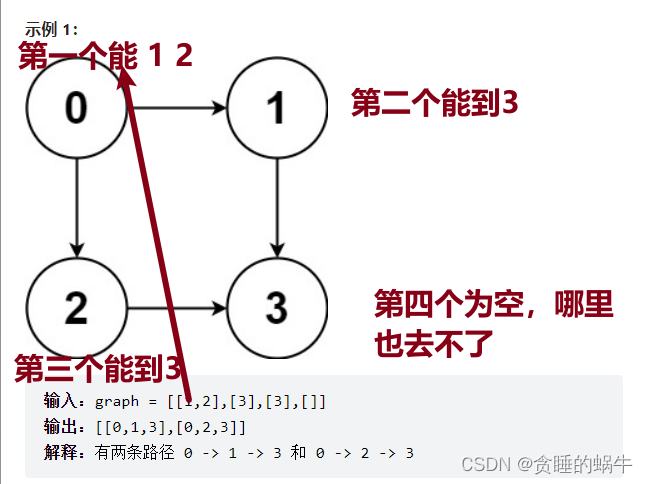
深度优先搜索,即递归
graph[node]是node节点能到的位置,这里用n去遍历它
因为题目中明确表示为无环图,所以不需要判断一个节点是否以及访问过
只要遍历的节点的数目达到n-1,那么就是一条路径
剑指 Offer II 111. 计算除法
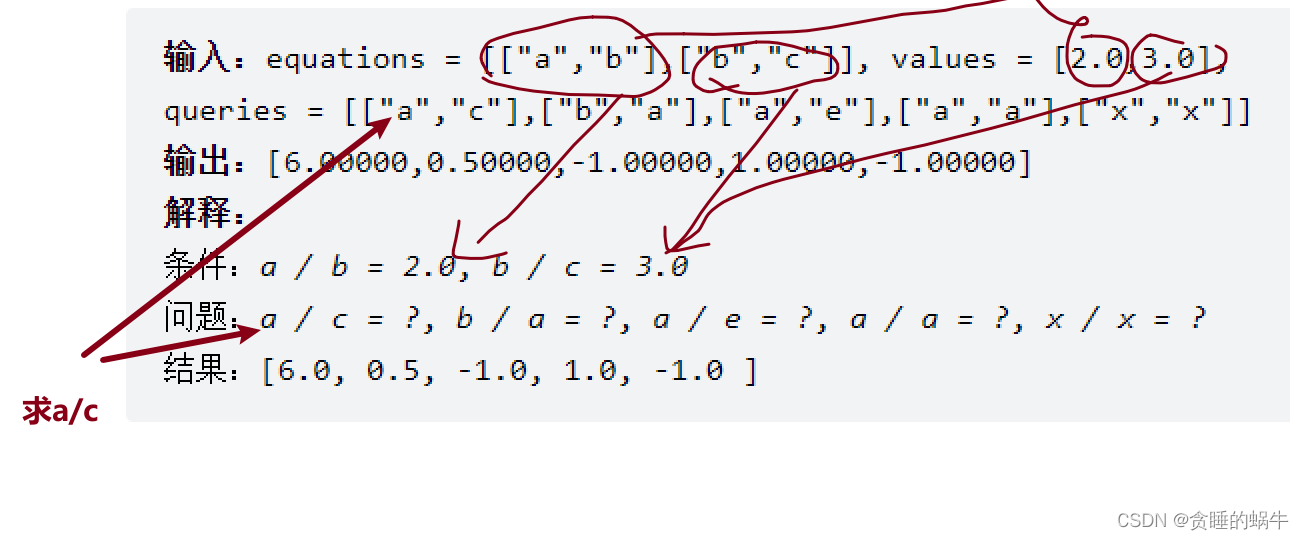
给定一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
注意:输入总是有效的。可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果
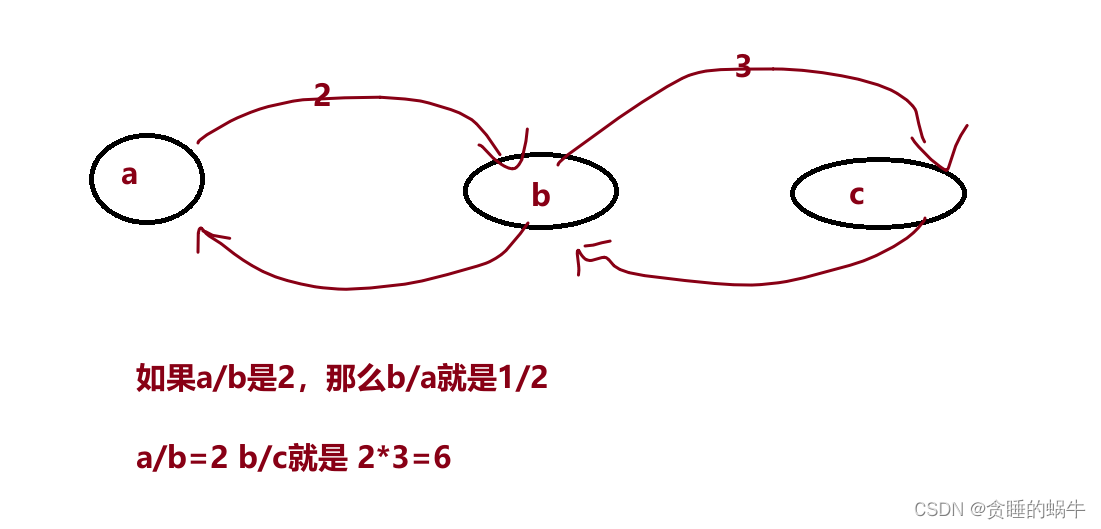
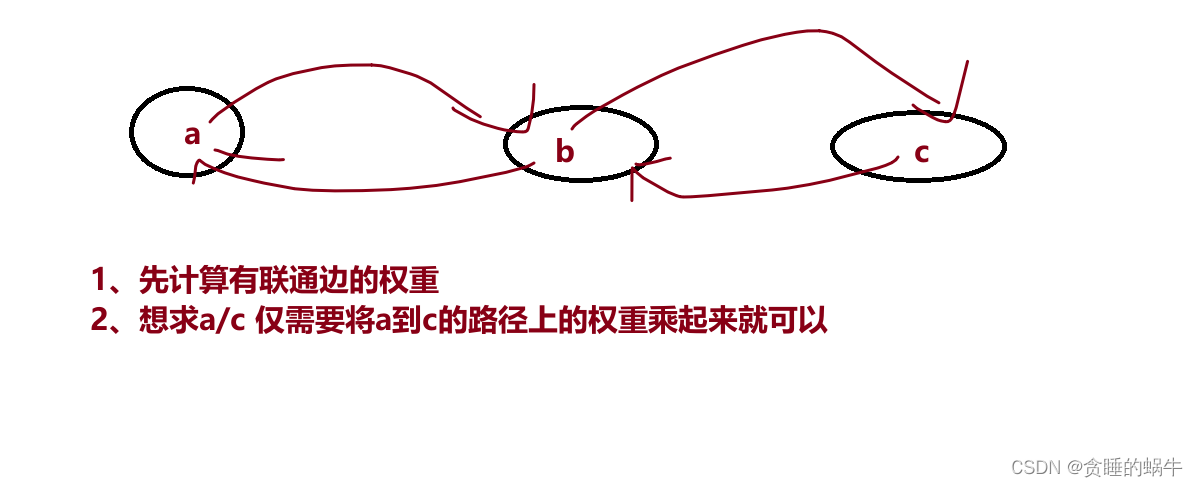

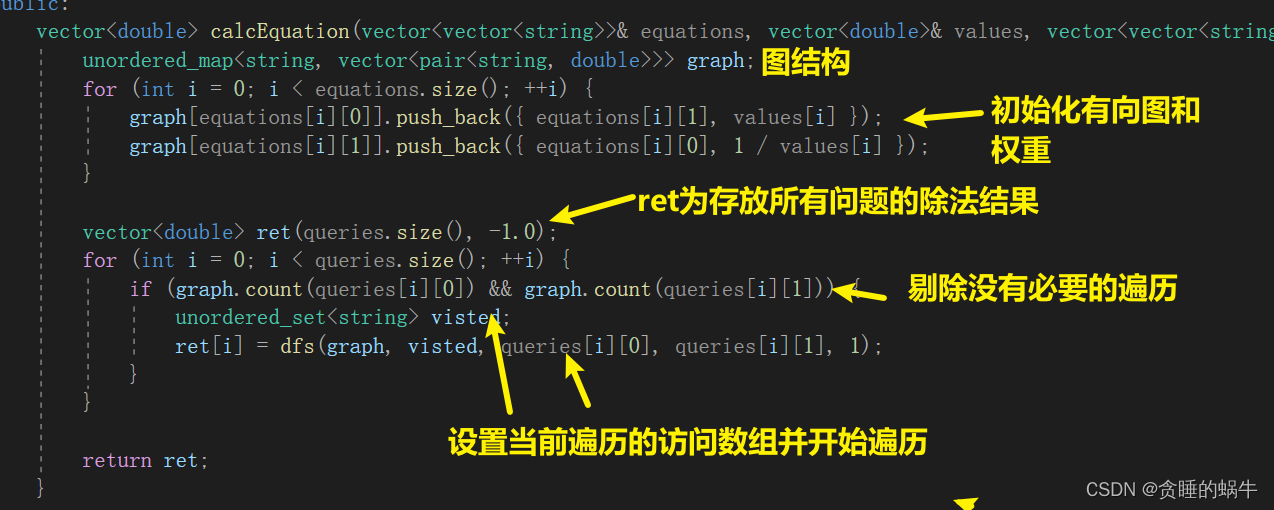
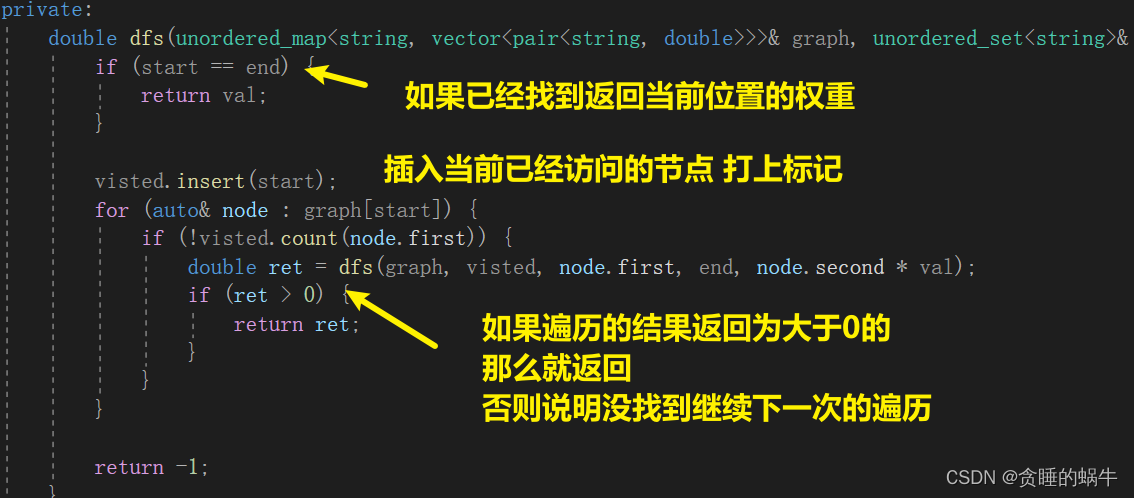
class Solution { private: double dfs(unordered_map<string, vector<pair<string, double>>>& graph, unordered_set<string>& visted, string start, string end, double val) { if (start == end) { return val; } visted.insert(start); //将新节点加入到visted中防止回头 for (auto& node : graph[start]) { //循环遍历图 if (!visted.count(node.first)) {//如果图的开始结点没有被访问过 double ret = dfs(graph, visted, node.first, end, node.second * val);//起点一直在变,终点没有改变 if (ret > 0) { //这个地方很关键,并不是直接返回而是进行判断 return ret; //如果大于 0 肯定可以直接返回,但如果小于 0, 只能说明当前元素作为起点无法与终点连通,应进行下一循环,换个起点 }如果直接返回 -1 就相当于断言没有通向终点的路径,并非如此,循环结束才能说明无法到达 } } return -1; } public: vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) { //graph第一个元素存放a,b这种节点,第二个元素存放到另外元素的权重的容器 unordered_map<string, vector<pair<string, double>>> graph; //equations[i][0]表示起始点,graph[equations[i][1]]表示终点,values[i]表示由起始到终点的权重 for (int i = 0; i < equations.size(); ++i) { graph[equations[i][0]].push_back({ equations[i][1], values[i] }); graph[equations[i][1]].push_back({ equations[i][0], 1 / values[i] }); } //用ret表示 -1.0是题目中表示没有通道的数 vector<double> ret(queries.size(), -1.0); for (int i = 0; i < queries.size(); ++i) { //对所有提出的问题进行遍历 if (graph.count(queries[i][0]) && graph.count(queries[i][1])) { //如果图中包含起始终点,就把-1.0更新否则不更新 unordered_set<string> visted; ret[i] = dfs(graph, visted, queries[i][0], queries[i][1], 1); } } return ret; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
剑指 Offer II 112. 最长递增路径
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
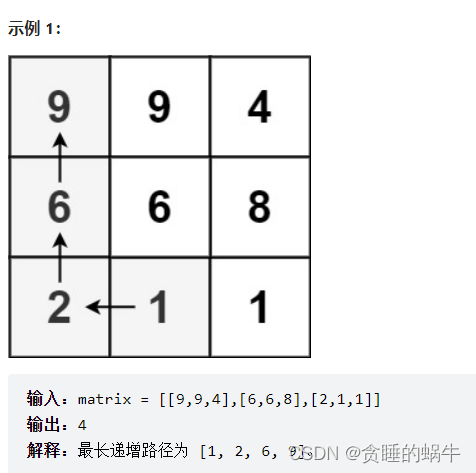
路径只要是递增的就行没有大小的限制,但路径必须是最长的。对每个点进行深度遍历
剑指 Offer II 113. 课程顺序
现在总共有 numCourses 门课需要选,记为 0 到 numCourses-1。
给定一个数组 prerequisites ,它的每一个元素 prerequisites[i] 表示两门课程之间的先修顺序。 例如 prerequisites[i] = [ai, bi] 表示想要学习课程 ai ,需要先完成课程 bi 。
请根据给出的总课程数 numCourses 和表示先修顺序的 prerequisites 得出一个可行的修课序列。
可能会有多个正确的顺序,只要任意返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
输入: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。用拓扑排序来做,但是题目的意思并不需要一条完整从开始到结束的路径,而是要包含所有节点且顺序要对,那么其实也就是将入度为0的加入节点,加入节点后删除从这个节点出发的其他节点的入度,
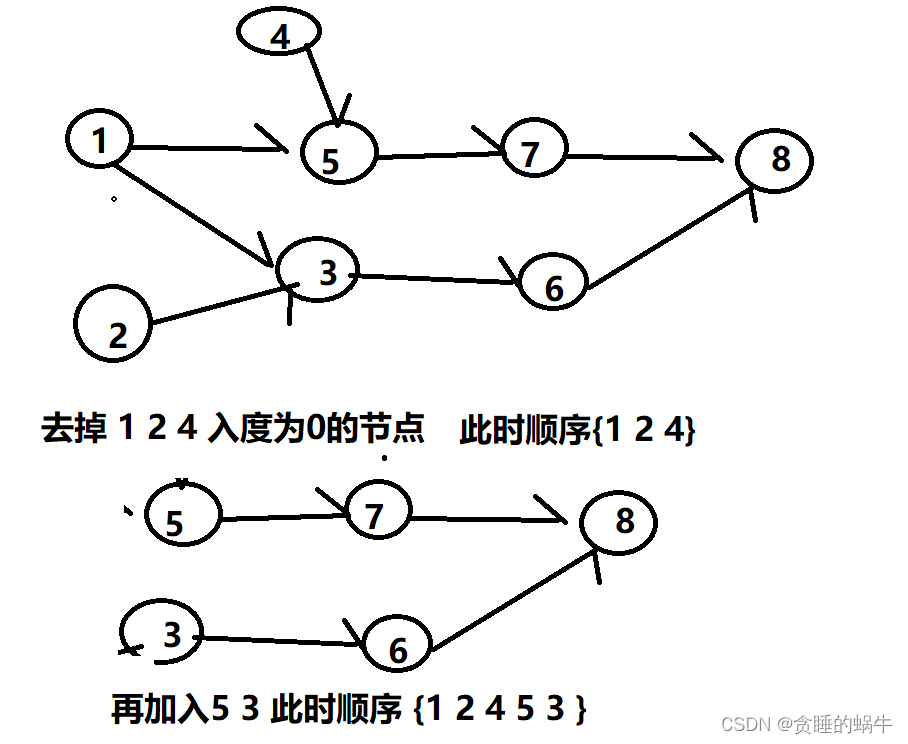

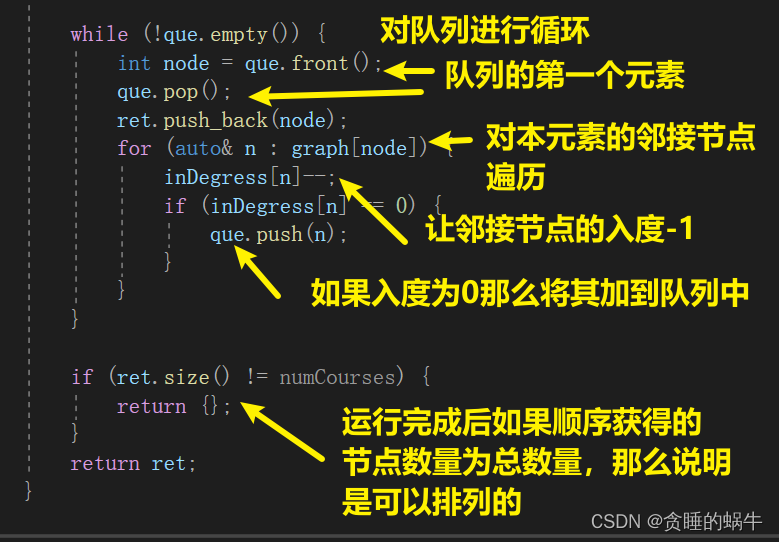
class Solution { public: vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) { //表示各节点的邻接表 unordered_map<int, vector<int>> graph; vector<int> inDegress(numCourses, 0); //保存入度 for (auto& pre : prerequisites) { //维护邻接表和入度为0的表 graph[pre[1]].push_back(pre[0]); inDegress[pre[0]]++; } vector<int> ret; queue<int> que; //队列保存入度为0的节点 for (int i = 0; i < inDegress.size(); ++i) { if (inDegress[i] == 0) { //如果入度为0将其加入排序序列 que.push(i); } } while (!que.empty()) { int node = que.front(); que.pop(); ret.push_back(node); for (auto& n : graph[node]) { inDegress[n]--; if (inDegress[n] == 0) { que.push(n); } } } if (ret.size() != numCourses) { return {}; } return ret; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
剑指 Offer II 114. 外星文字典
现有一种使用英语字母的外星文语言,这门语言的字母顺序与英语顺序不同。
给定一个字符串列表 words ,作为这门语言的词典,words 中的字符串已经 按这门新语言的字母顺序进行了排序 。
请你根据该词典还原出此语言中已知的字母顺序,并 按字母递增顺序 排列。若不存在合法字母顺序,返回 “” 。若存在多种可能的合法字母顺序,返回其中 任意一种 顺序即可。
字符串 s 字典顺序小于 字符串 t 有两种情况:
在第一个不同字母处,如果 s 中的字母在这门外星语言的字母顺序中位于 t 中字母之前,那么 s 的字典顺序小于 t 。
如果前面 min(s.length, t.length) 字母都相同,那么 s.length < t.length 时,s 的字典顺序也小于 t 。输入:words = [“wrt”,“wrf”,“er”,“ett”,“rftt”]
输出:“wertf”题目意思是words里的单词已经按顺序排好了,比如第二个和第三个但是,说w和
e,w更往前,对第一个和第二个说t比f在前面。题目要求将外星语的单词字母的顺序找出来
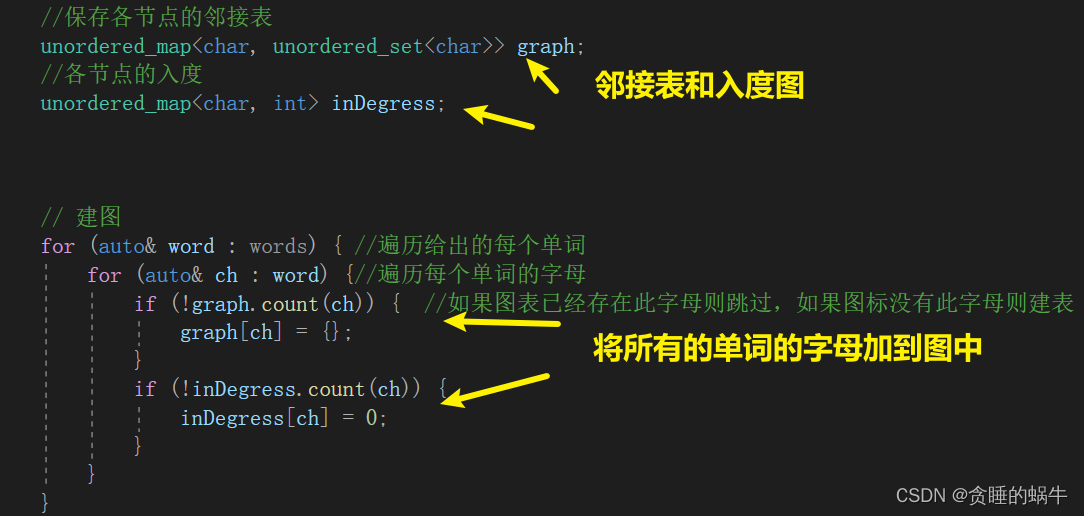
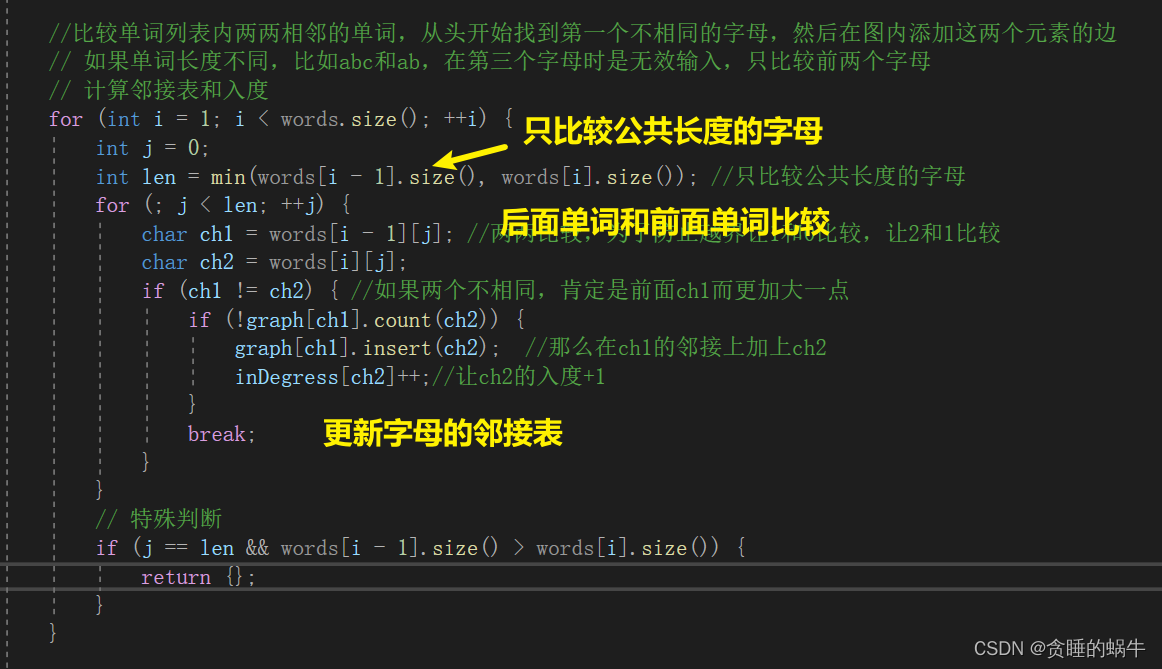
下面遍历队列的就不看了和上上题类似剑指 Offer II 115. 重建序列
给定一个长度为 n 的整数数组 nums ,其中 nums 是范围为 [1,n] 的整数的排列。还提供了一个 2D 整数数组 sequences ,其中 sequences[i] 是 nums 的子序列。
检查 nums 是否是唯一的最短 超序列 。最短 超序列 是 长度最短 的序列,并且所有序列 sequences[i] 都是它的子序列。对于给定的数组 sequences ,可能存在多个有效的 超序列 。例如,对于 sequences = [[1,2],[1,3]] ,有两个最短的 超序列 ,[1,2,3] 和 [1,3,2] 。
而对于 sequences = [[1,2],[1,3],[1,2,3]] ,唯一可能的最短 超序列 是 [1,2,3] 。[1,2,3,4] 是可能的超序列,但不是最短的。
如果 nums 是序列的唯一最短 超序列 ,则返回 true ,否则返回 false 。
子序列 是一个可以通过从另一个序列中删除一些元素或不删除任何元素,而不改变其余元素的顺序的序列。输入:nums = [1,2,3], sequences = [[1,2],[1,3],[2,3]]
输出:true
解释:最短可能的超序列为[1,2,3]。
序列 [1,2] 是它的一个子序列:[1,2,3]。
序列 [1,3] 是它的一个子序列:[1,2,3]。
序列 [2,3] 是它的一个子序列:[1,2,3]。
因为 nums 是唯一最短的超序列,所以返回true。剑指 Offer II 116. 省份数量

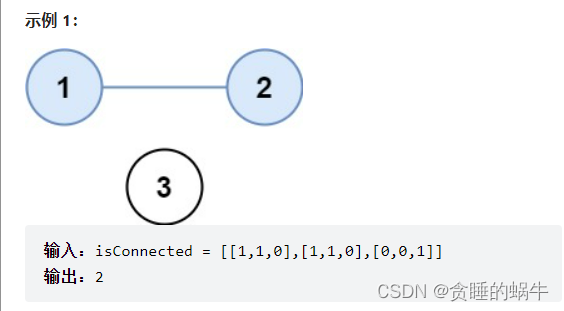
用二维数组表示行和列有没有边相连
返回子图的个数,上图有两个子图所以返回2方法一 广度优先搜索
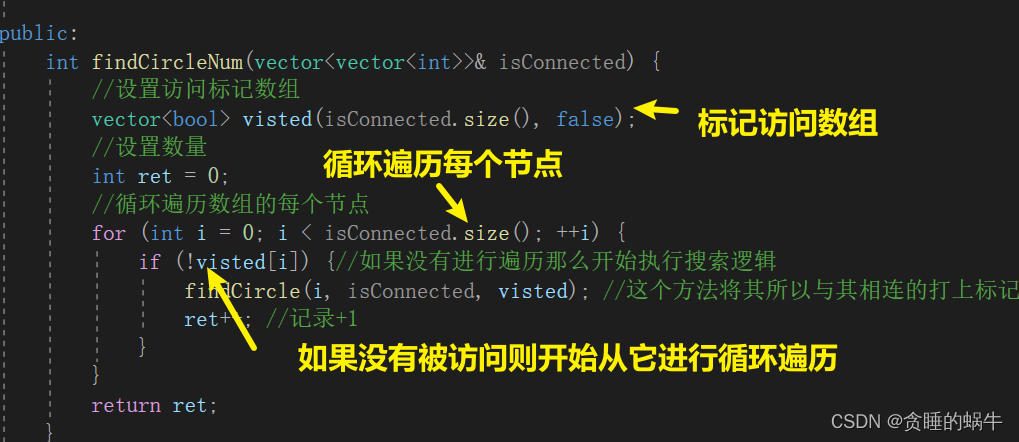
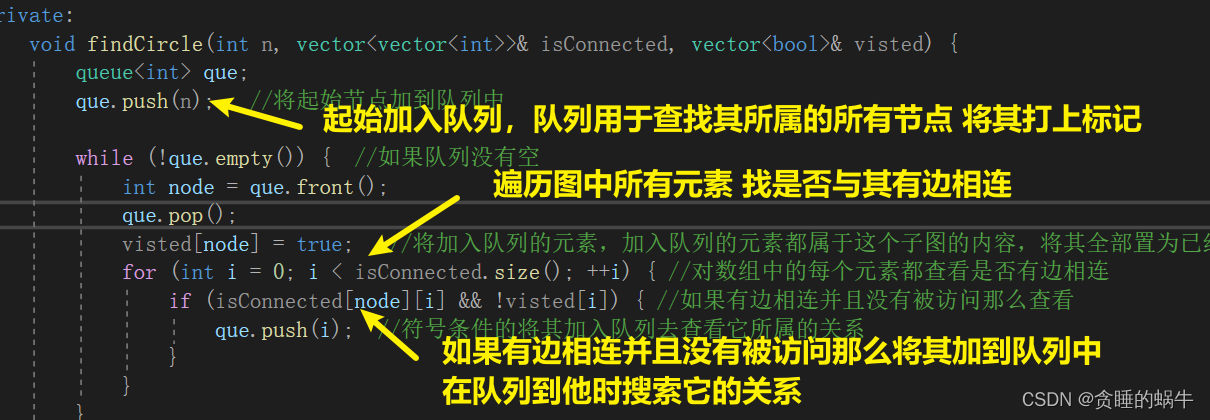
方法二 并查集
看大佬的笔记并查集
并查集概念主要用于解决一些元素分组的问题。它管理一系列不相交的集合,并支持两种操作:
合并(Union):把两个不相交的集合合并为一个集合。
查询(Find):查询两个元素是否在同一个集合中。并查集的重要思想在于,用集合中的一个元素代表集合。我曾看过一个有趣的比喻,把集合比喻成帮派,而代表元素则是帮主。接下来我们利用这个比喻,看看并查集是如何运作的。
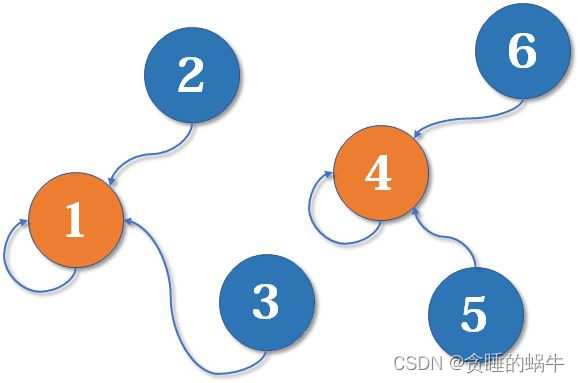
各自合并,如果有一个加入帮派中那么其所有的弟子都会加入这个帮派。这是一个树状的结构,要寻找集合的代表元素,只需要一层一层往上访问父节点(图中箭头所指的圆),直达树的根节点(图中橙色的圆)即可。
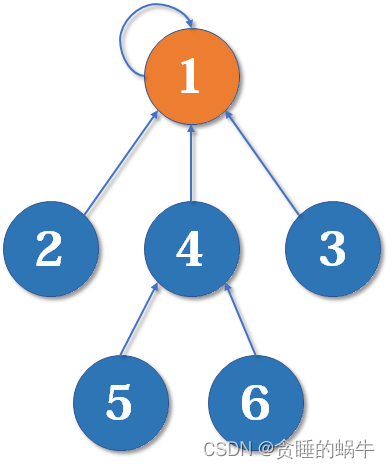
1、初始化,各自为战
int fa[MAXN]; inline void init(int n) { for (int i = 1; i <= n; ++i) fa[i] = i; }- 1
- 2
- 3
- 4
- 5
- 6
2、查询
用递归的写法实现对代表元素的查询:一层一层访问父节点,直至根节点(根节点的标志就是父节点是本身)。要判断两个元素是否属于同一个集合,只需要看它们的根节点是否相同即可。int find(int x) { if(fa[x] == x) return x; else return find(fa[x]); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
3、合并
合并操作也是很简单的,先找到两个集合的代表元素,然后将前者的父节点设为后者即可。inline void merge(int i, int j) { fa[find(i)] = find(j); }- 1
- 2
- 3
- 4
3.1 路径压缩
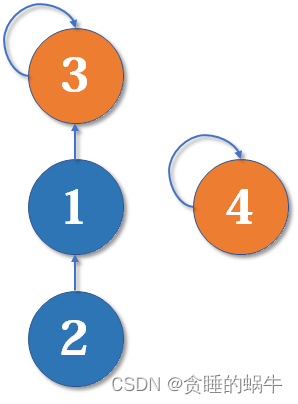
上图如果2和4合并,那么就需要从2找到1,再从1找到3然后3和4合并,形成下面这样

这样可能会形成一条长长的链,随着链越来越长,我们想要从底部找到根节点会变得越来越难。
可以使用路径压缩的方法。既然我们只关心一个元素对应的根节点,那我们希望每个元素到根节点的路径尽可能短,那么可以让每个节点和根节点直接相连。

这样查找就可以通过
int find(int x) { return x == fa[x] ? x : (fa[x] = find(fa[x])); }- 1
- 2
- 3
- 4
3.2 按秩合并
并查集并不一定都是两层的树,现在我们有一棵较复杂的树需要与一个单元素的集合合并,如果我们可以选择的话,是把7的父节点设为8好,还是把8的父节点设为7好呢?
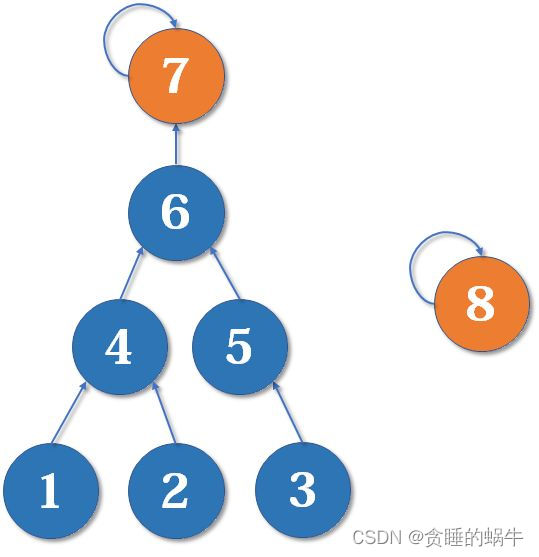
自然是将7当为父节点,这样就少盖了一层。
我们用一个数组rank[]记录每个根节点对应的树的深度(如果不是根节点,其rank相当于以它作为根节点的子树的深度)。一开始,把所有元素的rank(秩)设为1。合并时比较两个根节点,把rank较小者往较大者上合并。并查集实现代码
0、改变其根节点
fa[i] = i+1;//将i的根节点设置为i+1- 1
1、初始化(按秩合并)
初始化为其是自身的根节点,它的秩设为1(深度)inline void init(int n) { for (int i = 1; i <= n; ++i) { fa[i] = i; rank[i] = 1; } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
2、合并(按秩合并)
将两个节点合并,先找到这两个节点的根节点,然后比较两个根的秩,小秩的依托大的秩inline void merge(int i, int j) { int x = find(i), y = find(j); //先找到两个根节点 if (rank[x] <= rank[y]) fa[x] = y; else fa[y] = x; if (rank[x] == rank[y] && x != y) rank[y]++; //如果深度相同且根节点不同,则新的根节点的深度+1 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
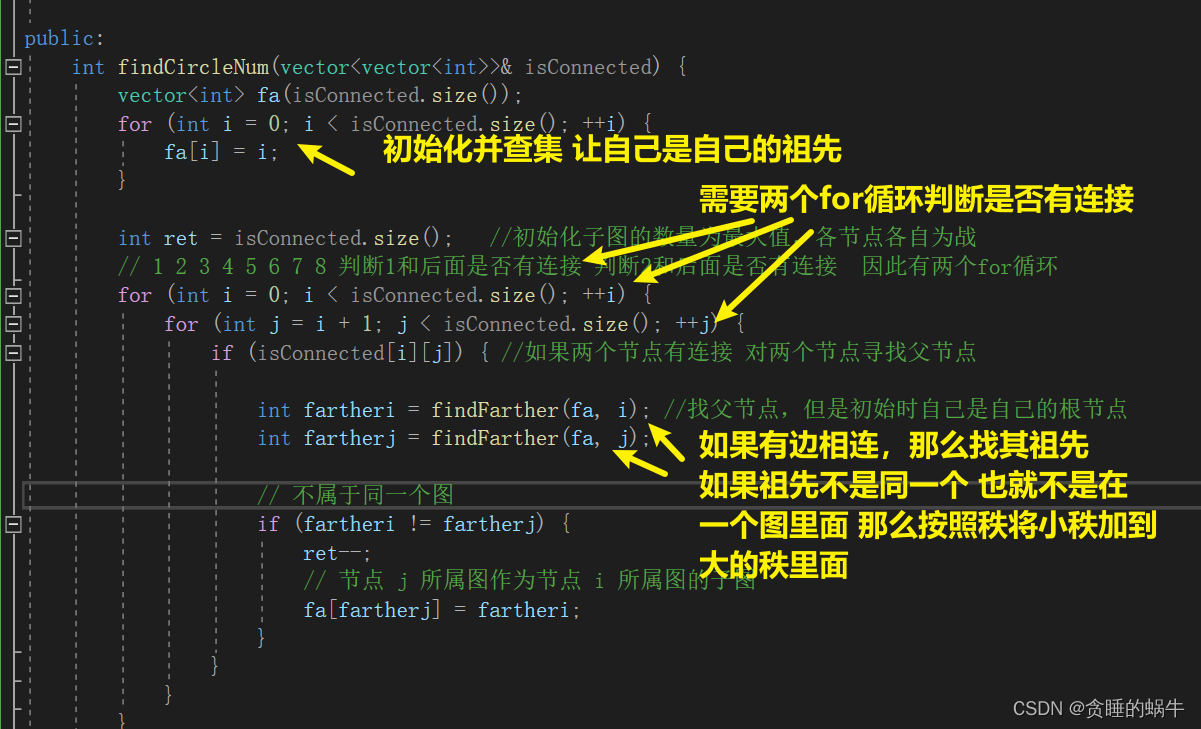
这个题的解法中层次只有二层
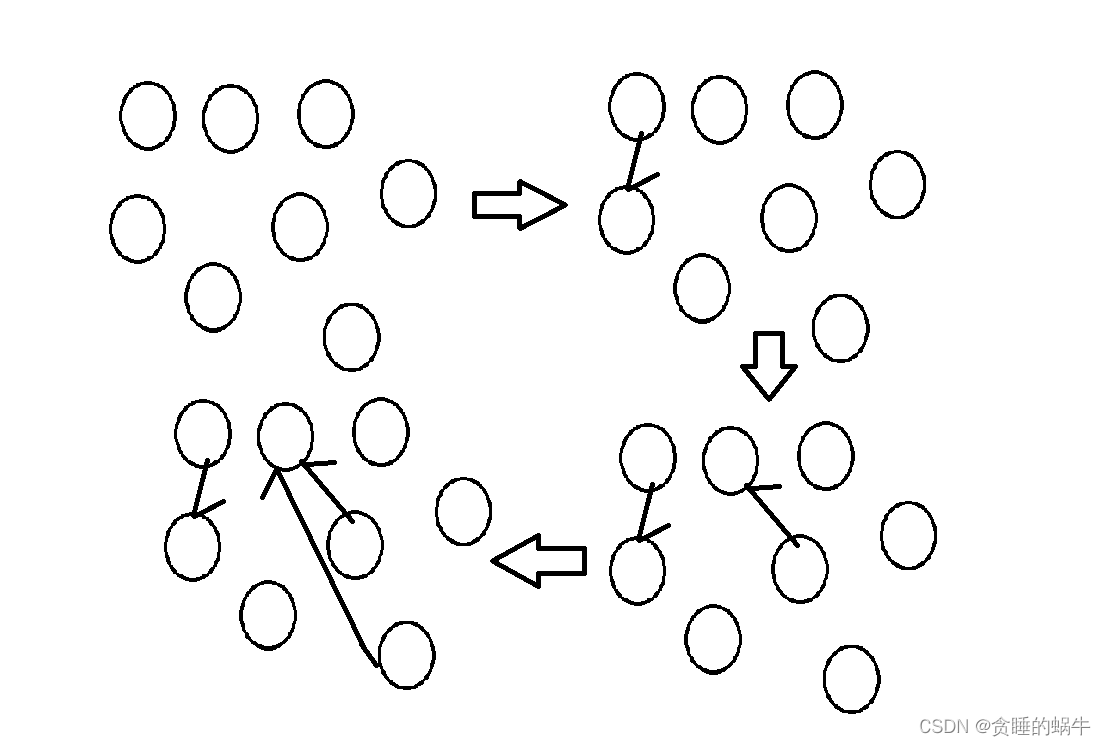

class Solution { private: int findFarther(vector<int>& fa, int node) { if (fa[node] == node) { //传递过来一个node初始节点,如果 return node; } fa[node] = findFarther(fa, fa[node]); return fa[node]; } public: int findCircleNum(vector<vector<int>>& isConnected) { vector<int> fa(isConnected.size()); for (int i = 0; i < isConnected.size(); ++i) { fa[i] = i; } int ret = isConnected.size(); //初始化子图的数量为最大值,各节点各自为战 // 1 2 3 4 5 6 7 8 判断1和后面是否有连接 判断2和后面是否有连接 因此有两个for循环 for (int i = 0; i < isConnected.size(); ++i) { for (int j = i + 1; j < isConnected.size(); ++j) { if (isConnected[i][j]) { //如果两个节点有连接 对两个节点寻找父节点 int fartheri = findFarther(fa, i); //找父节点,但是初始时自己是自己的根节点 int fartherj = findFarther(fa, j); // 不属于同一个图 if (fartheri != fartherj) { ret--; // 节点 j 所属图作为节点 i 所属图的子图 fa[fartherj] = fartheri; } } } } return ret; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
剑指 Offer II 117. 相似的字符串
如果交换字符串 X 中的两个不同位置的字母,使得它和字符串 Y 相等,那么称 X 和 Y 两个字符串相似。如果这两个字符串本身是相等的,那它们也是相似的。
例如,“tars” 和 “rats” 是相似的 (交换 0 与 2 的位置); “rats” 和 “arts” 也是相似的,但是 “star” 不与 “tars”,“rats”,或 “arts” 相似。
总之,它们通过相似性形成了两个关联组:{“tars”, “rats”, “arts”} 和 {“star”}。注意,“tars” 和 “arts” 是在同一组中,即使它们并不相似。形式上,对每个组而言,要确定一个单词在组中,只需要这个词和该组中至少一个单词相似。
给定一个字符串列表 strs。列表中的每个字符串都是 strs 中其它所有字符串的一个 字母异位词 。请问 strs 中有多少个相似字符串组?
字母异位词(anagram),一种把某个字符串的字母的位置(顺序)加以改换所形成的新词。
输入:strs = [“tars”,“rats”,“arts”,“star”]
输出:2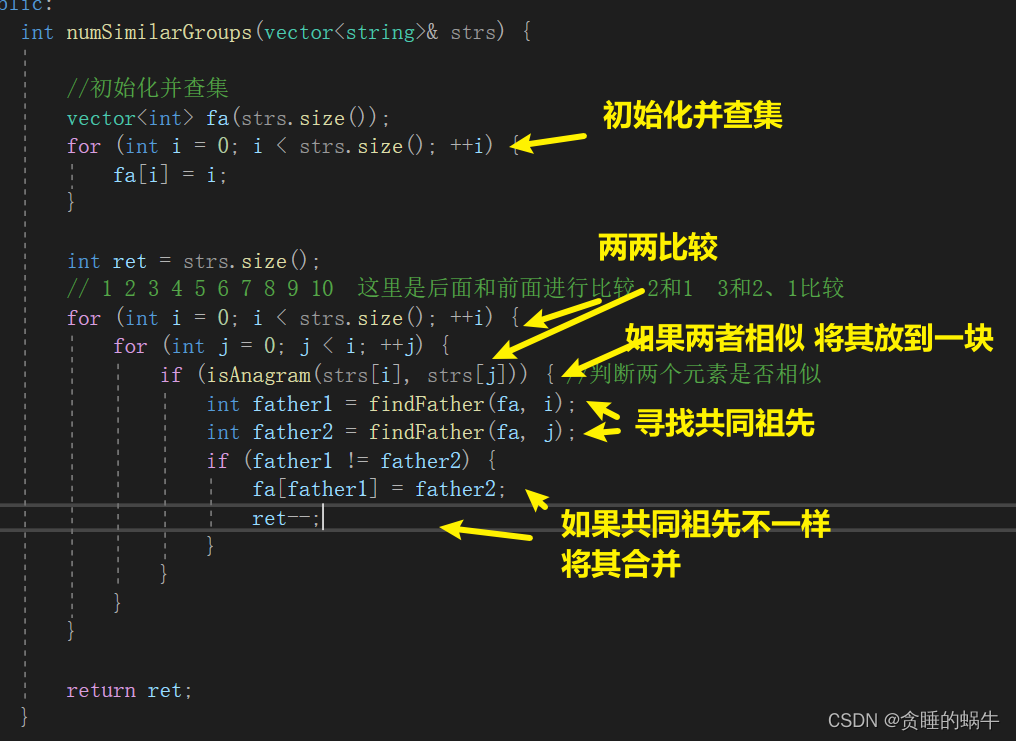

剑指 Offer II 118. 多余的边
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
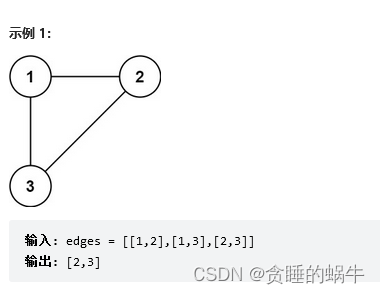
上面1 2表示1个2有一条边,1 3表示1和3有一条边,2,3表示2和3有一条边
要求删除一条边让其变成一个最简略的树
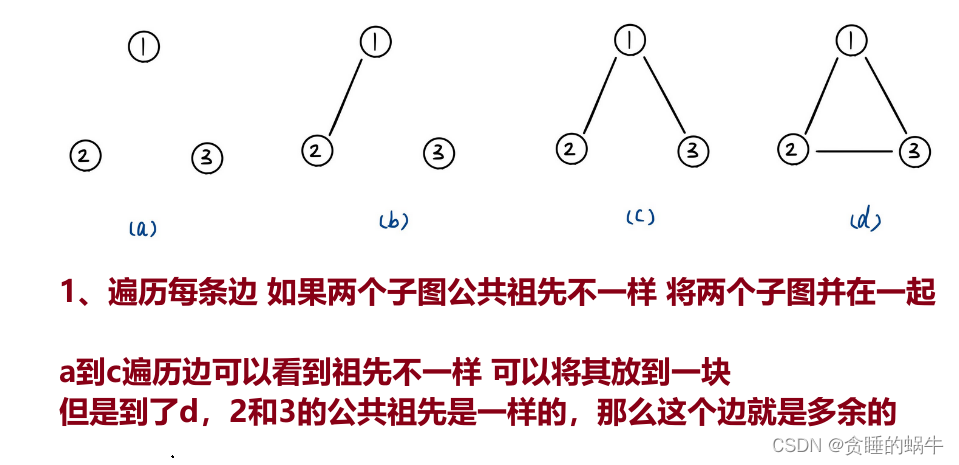
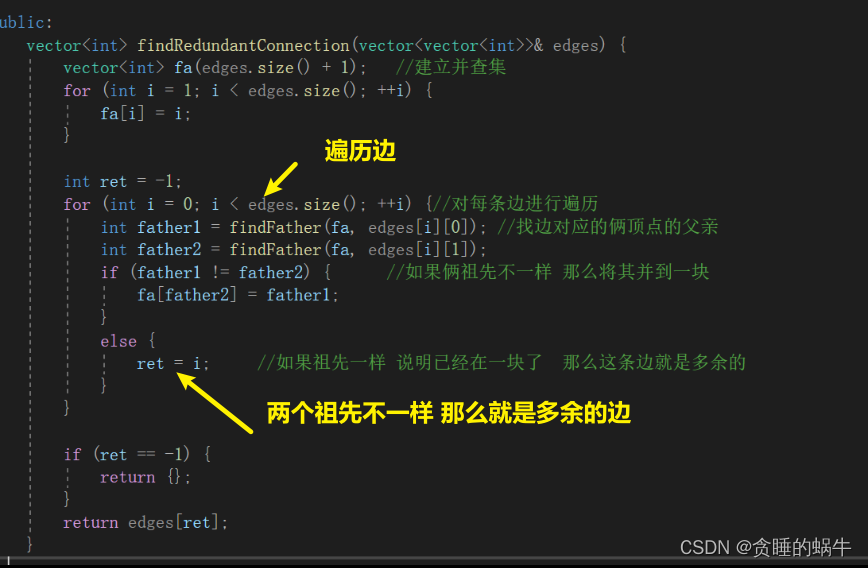
剑指 Offer II 119. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。

输入数字有1 2 3 4 ,它是连续的 所以最长连续数字序列是4相差为1的两个数有一条边,这样就分成了若干子图,然后去求最大的子图
方法一:图的广度优先搜索

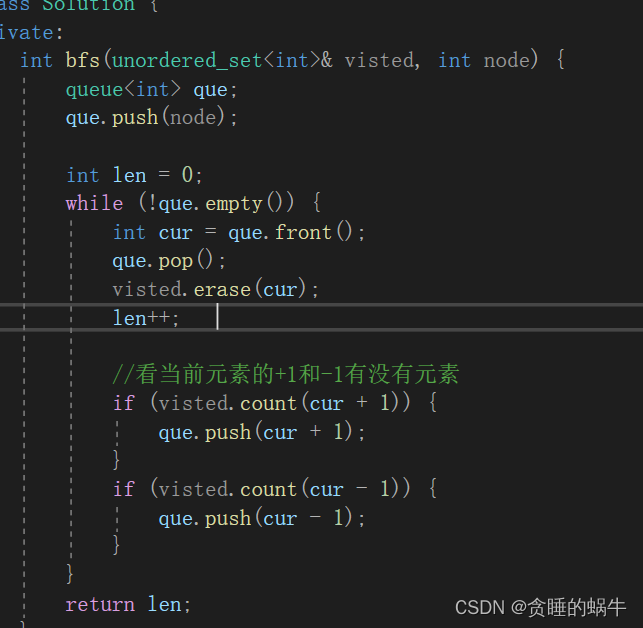
方法二:并查集
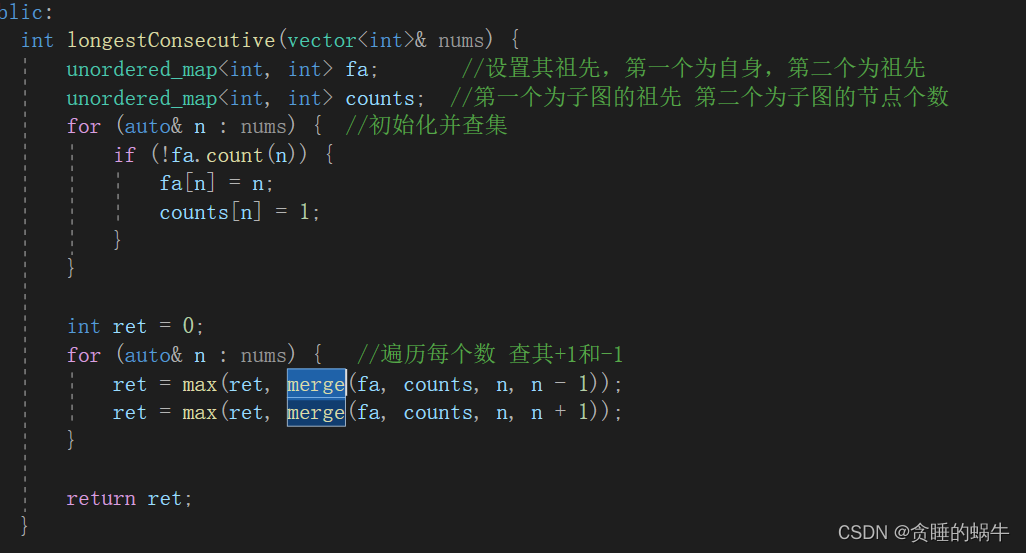

-
相关阅读:
算法进修Day-34
《30天吃掉那只 TensorFlow2.0》五、TensorFlow的中阶API
Hadoop启动后jps发现没有DateNode解决办法
谷粒商城1.项目简介和项目环境预搭建(项目概述和环境搭建代码)
c++ STL:关于 std::vector 的移除删除函数remove()和erase()的使用
Linux下Clock skew detected的解决办法 && Linux时间戳和标准时间的互转
CF 1708A/数学思维
十分钟带你入门向量检索技术
model字体图标
docker 下安装mysql8.0
- 原文地址:https://blog.csdn.net/baidu_41553551/article/details/126596293
