-
因果系列文章(5)——干预
本节我们一起学习有关干预(intervention)的概念。首先,我们介绍一种更加完善而正规的因果图模型——结构因果模型(Structural Causal Model, SCM),然后引入干预的概念,介绍do运算的操作。最后,我们用干预的方式来解释一个非常令人困惑的混杂现象——辛普森悖论。
结构因果模型
首先,我们给出结构因果模型的定义:结构因果模型包含两个变量集合 U 和 V ,以及一组函数 f ,该函数对变量集 V 中的每一个变量进行赋值。
进一步地,因果关系也可以更加正式的被定义:变量 X 是变量 Y 的直接原因(direct cause),如果 X 出现在对 Y 进行赋值的函数中。如果,X 是 Y 的直接原因,或者是 Y 的任何一个原因的原因,那么 X 就是 Y 的原因(cause)。
集合 U 中的变量被称为外生变量(exogenous variables),意思是这些变量是在模型外部存在的,我们不关心它们的因是什么。集合 V 中的变量被称为内生变量(endogenous variables)。模型中的每一个内生变量都是至少一个外生变量的后代。外生变量不能是其他变量的后代,特别是不能是内生变量的后代,它们没有祖先,在图中外生变量就是根节点。如果我们知道每一个外生变量的值,那么利用 f 中的函数,我们就可以完全确定每一个内生变量的值。
每一个SCM都有一个图模型与之对应。图模型中的节点就代表SCM的集合 U 和 V 中的变量,图模型中的边就代表SCM中的函数 f 。一个SCM M 的图模型 G 中每一个节点表示 M 中的每一个变量,如果 M 中有关变量 X 的函数 fX 包含了变量 Y (也即 X 依赖于 Y 的值),那么在图模型 G 中 Y 与 X 之间就有一条边。在一个图形模型中,如果一个变量 X 是另一个变量 Y 的子节点,那么 Y 就是 X 的一个直接原因;如果 X 是 Y 的后代节点,那么 Y 就是 X 的潜在原因。
【例1】图1所示的SCM模型反应了“工资”Z 与“教育背景”X 和“工作经验”Y 的关系。
U={X,Y},V={Z},F={fZ}
fZ:Z=2X+3Y
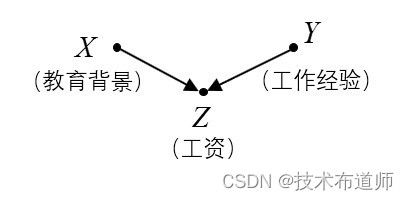
图1:例1
与之前几节的例子不同,我们假设这里的三个变量都是连续变量。例如这个模型中, Z 代表了雇主付给一个员工的工资, X 代表这个人接受教育的年限, Y 代表这个人的工作年限。 X 和 Y 都出现在 fZ 中,所以 X 和 Y 都是 Z 的直接原因。如果 X 和 Y 有祖先,那么这些祖先就是 Z 的潜在原因。
由于 Z 和 X 、 Z 和 Y 之间有边连接,所以我们仅通过观察图模型就可以得出结论:有某个函数 fZ 基于 X 和 Y 来对 Z 进行赋值。因此&
-
相关阅读:
Markdown数学公式大全
高级IO-epoll
关于产品和消费的思考
lua-web-utils和proxy程序示例
强化学习 (三) 动态规划
论企业数字化和IT组织思考
Java—Map
ubuntu22.04.1 新装后的常用设置
Linux shell printf命令小例子
基于 ResNet18 架构使用 deformable convolution的车道线检测
- 原文地址:https://blog.csdn.net/jiey0407/article/details/126642207