计算机视觉入门-最小二乘法、随机取样法、鲁棒估计、霍夫变换

第三章 拟合(Fitting)

就是为了给定数学公式生成线来描述图像

首先我们对图片处理可能会受到三个方面的影响：

1.噪声 偏离正确位置

2.无关数据 就是不属于检测物体的轮廓线

3.遗漏数据 因为遮挡等原因 无法检测到

问题：

1.如果某点属于某条线，如何找出

最小二乘法

2.如果有噪声点

噪声点少：Robust fitting

噪声点多：RANSAC

3.很多条线

RANSAC， Hough transform(一次性把噪声线提出)

最小二乘(Least squares) & RANSAC(随机采样一致性)

最小二乘(Least squares)：

问题就是所有的点都处于线上

公式

描述点到线Y轴的距离。E越小表示点距离线越近。使其达到最小，也就是需要m,b两个值

那就可以设

Y = XB（线性代数矩阵乘法）

对B求导

若B可逆则可以得到B的表达式，再利用矩阵乘法可以得到B的矩阵

问题：

1.不能描述垂直线

2.不能旋转

全最小二乘(Total least squares)

计算的是点到直线的距离（从几何上来建模）

对d求导可以得到

再代入原式中可得：

也就是求最小特征值所对应的特征向量

也就是某点至设置点在法向量上的投影最短

最小二乘以极大似然估计来表示(Least squares as likelihood maximization)

也就是从概率方面来建模看待问题

就是沿着真实点的法向量由噪声引起的偏差点，ε是为点在真实点附近的概率

二者关系为正比例

使用对数似然方程（由于独立同分布的样本的似然函数上具有连乘积，对似然方程取对数更方便计算）最终可得到：

因为为负，要使其达到最大，则分子要达到最小。又回到最小二乘的问题上。

鲁棒估计(Robust estimators)

通过控制ε来决定距离线多远的点不再考虑

ρ是对E进行处理，超过这个值就不再处理

r就是各个点到直线的距离 θ包含了a, b ,d， 而xi则是已知的

处理结果：

如果参数选择太小，最远的点与稍远的点相同，都不会

如果参数选择过大。点距离越大，贡献越大。

特性：

1.是一个非线性优化问题

2.自适应的方法（用最小二乘求出基础的a,b,d）

Random sample consensus(RANSAC)(随机采样一致性)方法

1.如果得到的点大多数点都属于外点

2.一种很通用的方法

步骤：

1.选择一个最小的集合（两个点确定一条直线）

2.得出一个数学模型（直线方程）

3.剩下的点对直线的距离如果都近，则为所求

4.重复以上三步（看哪个直线距离的点最多）

举例：

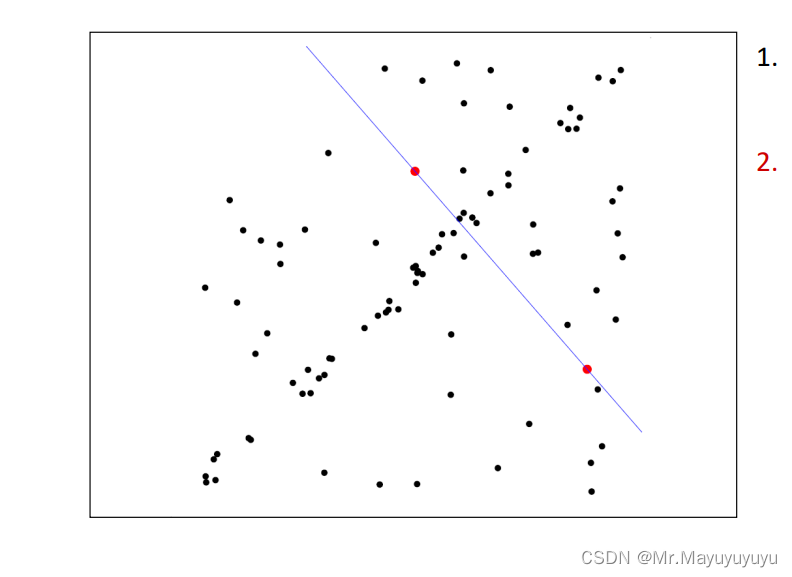
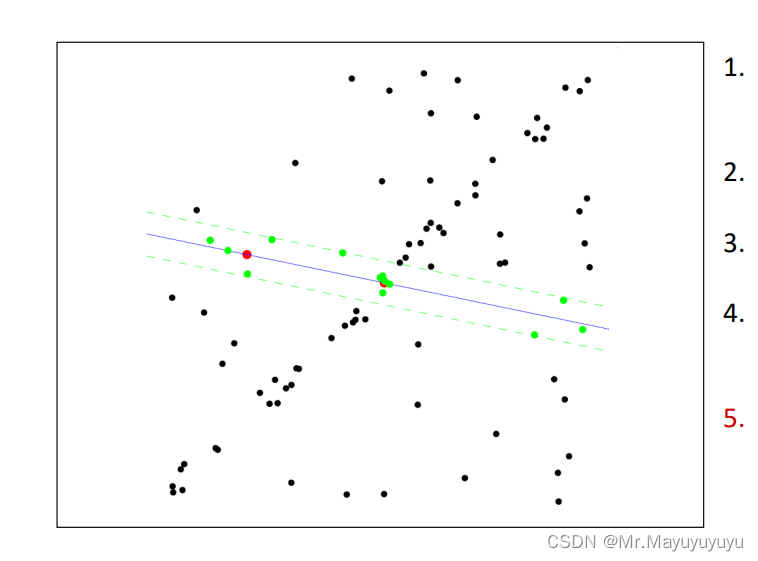
重复N次过程：

1.随机找出s点

2.用找出的s点来拟合直线

3.找到类点，就是设置点到直线的距离不超过t（门限值t）

4.如果找出距离点的个数d比之前的d多的话，取d

公式：

P为所需要数学模型的正确率

e是不属于这个线上的点的概率

而S次方表示这次采样正确的概率

N次方表示采样N次

则N就可以表示为

此表s表示确定几个点可以确定直线

概率表示有多少内点，所对应的数字表示需要迭代的次数

自适应算法的步骤：

1.首先设置迭代次数N为无穷

2.当迭代次数少于N时 选一个点计算内点率，通过类点率计算外点率。外点率肯定比无穷小，所以采样数+1

3.可以的得到一条直线l1,内点数d,所以可以得出N1，且迭代1次

其原理就是不断迭代，找到更好的线N的次数就会下降。如果找不到更好的就把当前的数学模型输出。一般N会设置固定值1000、10000等

拟合：霍夫变换(The Hough transform)

是一种投票的思想

首先图像空间中的直线对应参数空间的一个点

而图像空间中的一个点对应参数空间的一条线

因为我们对参数空间进行离散之后，就会出现N个m,b点决定了一条直线

但是存在问题

1.直线不好表达

2.参数空间存在边界

所以可以通过极坐标系来表达：

m,b不知道从哪开始，而根据ρθ坐标轴可以找到最小最大范围

找到最大的(ρ，θ)点之后，最终可以找到实现方程

问题：

噪声会引起偏差如：

解决噪声方法：
1.对空间区域进行离散

2.对点的邻居点进行投票

3.利用在边上的点(Canny算子把很多伪边剔除掉了)

改进方法：

也就是选择的θ的范围变小了。已知(x,y)，代入公式

由于不知道θ范围，我们可以进行投票得到参数图像：

由Canny算子可以得到梯度方向，所以可以得到θ点

圆的霍夫变换(Hough transform for circles)

流程：

当已知半径时，我们可以在图像空间中找到两个点

如果没有梯度方向那么在霍夫空间的面上就是一个圆面

位于图像空间中的外部与内部

通过从小到大变化r (x,y)所对应的(u,v)也会随之变化

通过不断变化，我们可以得到投票最高的(u,v,r)也是方程的解

实际运用：

每个图形代表着物体特征。可以比作车灯、车窗等

而这三类图像特征与中心点的关系可以看为：

三类图形依次进行拟合关系学习可以得到每个图形的

回到原图形，则可以得到给中心投票的结果：

霍夫变换

优势：

1.可以解决全局问题

2.可以解决多个实例

3.噪声点投票不会集中到几个格子上，使其随机的给多个离散区域投票

缺点：

1.最多应用于二维空间，三维空间做投影复杂

2.噪声造成的统一投票也会造成影响。很难避免

3.离散化（过大：损失精度 过小：投票值超不过门限）

解决离散化可以使用软投票法（把一个图像量化到另一图像，都可以使用此方法）

软投票：就是通过计算权重分散给临近区域，而非此点