数据挖掘学习笔记02——算法（分类、聚类、回归、关联）

前言

笔记来源于系统学习以下课程：
B站最完整系统的Python数据分析-数据挖掘教程，72小时带你快速入门，轻松转行（月入10W+数据分析师强烈推荐！）

分类算法

KNN算法

算法内容跳过~~

算法的优点：

1. 简单易实现
2. 对于边界不规则的数据效果较好

算法的缺点：

1. 只适合小数据集
2. 数据平衡效果不好
3. 必须要进行标准化
4. 不适合特征维数太多的数据
5. K值的选择会影响到模型的效果：K越小的时候容易过拟合；K越大的时候容易欠拟合

示例代码：

from sklearn import datasets  # sklearn的数据库
from sklearn.neighbors import KNeighborsClassifier  # sklearn模板的KNN类
import numpy as np  # 矩阵运算库

np.random.seed(0)
# 设置随机种子，不设置的话默认是按系统实践作为参数，设置后可以保证我们每次产生的随机数是一样的

iris = datasets.load_iris()  # 获取鸢尾花数据集
iris_x = iris.data  # 数据部分
iris_y = iris.target  # 类别部分
# 从150条数据中选140条作为训练集，10条作为测试集。permutation接收一个数作为参数（这里为数据集长度150），产生一个0-149乱序一维数组
randomarr = np.random.permutation(len(iris_x))
iris_x_train = iris_x[randomarr[:-10]]  # 训练集数据
iris_y_train = iris_y[randomarr[:-10]]  # 训练集数据
iris_x_test = iris_x[randomarr[-10:]]  # 测试集数据
iris_y_text = iris_y[randomarr[-10:]]  # 测试集数据

# 定义一个KNN分类器对象
knn = KNeighborsClassifier()
# 调用该对象的训练方法，主要接收两个参数：训练数据集及其类别标签
knn.fit(iris_x_train, iris_y_train)

# 调用预测方法，主要接收一个参数：测试数据集
iris_y_predict = knn.predict(iris_x_test)

# 计算各测试样本预测的概率值，这里我们没有使用概率值，但是在实际工作中可能会参考概率值来进行最后结果的筛选，而不是直接使用给出的标签数据集
probility = knn.predict_proba(iris_x_test)

# 计算与最后一个测试样本距离最近的5个点，返回的是这些样本的序号组成的数组
score = knn.score(iris_x_test, iris_y_text, sample_weight=None)

# 输出测试的结果
print('iris_y_predict=')
print(iris_y_predict)

# 输出原始测试数据集的正确标签，以方便对比
print('iris_y_text')
print(iris_y_text)

# 输出准确率结果
print('Accuracy:',score)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

代码运行结果：

iris_y_predict=
[1 2 1 0 0 0 2 1 2 0]
iris_y_text
[1 1 1 0 0 0 2 1 2 0]
Accuracy: 0.9
1
2
3
4
5

决策树

算法内容跳过~~

算法的优点：

1. 非常直观，可解释性极强
2. 预测速度比较快
3. 既可以处理离散值，也可以处理连续值，还可以处理缺失值

算法的缺点：

1. 容易过拟合（预剪枝、后剪枝）
2. 需要处理样本不均衡问题
3. 样本的变化会引发树结构的巨变
   

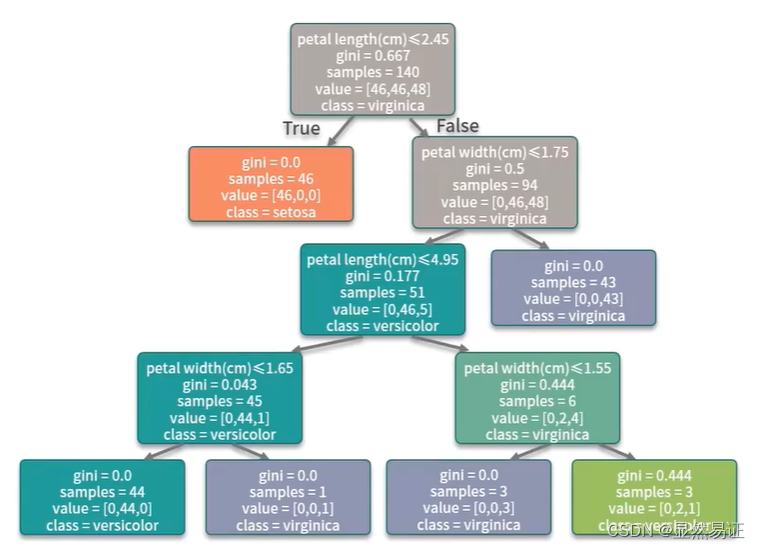
示例代码：

from sklearn import datasets  # sklearn的数据库
from sklearn.tree import DecisionTreeClassifier  # 引入决策树算法包
import numpy as np

# 引入相关画图的包
from IPython.display import Image
from sklearn import tree
# dot是一个程式化生成流程图的简单语言
import pydotplus


np.random.seed(0)
iris = datasets.load_iris()
iris_x = iris.data
iris_y = iris.target
indices = np.random.permutation(len(iris_x))
iris_x_train = iris_x[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_x_test = iris_x[indices[-10:]]
iris_y_text = iris_y[indices[-10:]]

# 设置树的最大深度为4
clf = DecisionTreeClassifier(max_depth=4)
clf.fit(iris_x_train, iris_y_train)

# 可视化
dot_data = tree.export_graphviz(clf, out_file=None, feature_names=iris.feature_names, class_names=iris.target_names,
                                filled=True, rounded=True, special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())

# 预测
iris_y_predict = clf.predict(iris_x_test)
score = clf.score(iris_x_test, iris_y_text, sample_weight=None)

print('iris_y_predict=')
print(iris_y_predict)
print('iris_y_test')
print(iris_y_text)
print('Accuracy:', score)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

这里代码有个坑：pydotplus.graphviz.InvocationException: GraphViz’s executables not found
可参考：可视化模块GraphViz’s executables not found报错解决

代码运行结果：

iris_y_predict=
[1 2 1 0 0 0 2 1 2 0]
iris_y_test
[1 1 1 0 0 0 2 1 2 0]
Accuracy: 0.9
1
2
3
4
5

扩展内容：

朴素贝叶斯

算法内容跳过~~

算法的优点：

1. 逻辑清晰简单、易于实现。适合大规模数据
2. 运算开销小
3. 预测过程快
4. 对于噪声点和无关属性比较健壮

算法的缺点：

1. 在具体应用的时候要考虑特征之间的相互独立性，再决定是否要用该算法

示例代码：

from sklearn import datasets  # sklearn的数据库
from sklearn.naive_bayes import GaussianNB  # 高斯分布型贝叶斯
import numpy as np
np.random.seed(0)
iris = datasets.load_iris()
iris_x = iris.data
iris_y = iris.target
indices = np.random.permutation(len(iris_x))
iris_x_train = iris_x[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_x_test = iris_x[indices[-10:]]
iris_y_text = iris_y[indices[-10:]]
clf = GaussianNB()  # 构造朴素贝叶斯分类器
clf.fit(iris_x_train, iris_y_train)  # 拟合

# 预测
iris_y_predict = clf.predict(iris_x_test)
score = clf.score(iris_x_test, iris_y_text, sample_weight=None)
print('iris_y_predict=')
print(iris_y_predict)
print('iris_y_test')
print(iris_y_text)
print('Accuracy:', score)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

代码运行结果：

iris_y_predict=
[1 2 1 0 0 0 2 1 2 0]
iris_y_test
[1 1 1 0 0 0 2 1 2 0]
Accuracy: 0.9
1
2
3
4
5

扩展内容：

支持向量机

算法内容跳过~~

算法的优点：

1. 有严格的数学理论支持，可解释性强
2. 算法的鲁棒性很好

算法的缺点：

1. 训练所需要的资源很大
2. 只能处理二分类问题
3. 模型预测时，预测时间与支持向量个数成正比

示例代码：

from sklearn import datasets
from sklearn import svm
import numpy as np

np.random.seed(0)
iris = datasets.load_iris()
iris_x = iris.data
iris_y = iris.target
indices = np.random.permutation(len(iris_x))
iris_x_train = iris_x[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_x_test = iris_x[indices[-10:]]
iris_y_text = iris_y[indices[-10:]]

# 模型
clf = svm.SVC(kernel='linear')
clf.fit(iris_x_train, iris_y_train)  # 拟合

# 预测
iris_y_predict = clf.predict(iris_x_test)
score = clf.score(iris_x_test, iris_y_text, sample_weight=None)
print('iris_y_predict=')
print(iris_y_predict)
print('iris_y_test')
print(iris_y_text)
print('Accuracy:', score)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

代码运行结果：

iris_y_predict=
[1 2 1 0 0 0 2 1 2 0]
iris_y_test
[1 1 1 0 0 0 2 1 2 0]
Accuracy: 0.9
1
2
3
4
5

人工神经网络

算法内容跳过~~

算法的优点：

1. 可以像搭积木一样不断地扩展模型的边界，而对于内部具体的运行不需要加以太多的干涉

算法的缺点：

1. 神经网络缺乏可解释性，它的内部纷繁复杂
2. 神经网络非常消耗资源

示例代码：

from sklearn import datasets
from sklearn.neural_network import MLPClassifier
import numpy as np

np.random.seed(0)
iris = datasets.load_iris()
iris_x = iris.data
iris_y = iris.target
indices = np.random.permutation(len(iris_x))
iris_x_train = iris_x[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_x_test = iris_x[indices[-10:]]
iris_y_text = iris_y[indices[-10:]]

# 模型
clf = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=(5, 2), random_state=1)
clf.fit(iris_x_train, iris_y_train)  # 拟合

# 预测
iris_y_predict = clf.predict(iris_x_test)
score = clf.score(iris_x_test, iris_y_text, sample_weight=None)
print('iris_y_predict=')
print(iris_y_predict)
print('iris_y_test')
print(iris_y_text)
print('Accuracy:', score)
print('layer nums:',clf.n_layers_)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

代码运行结果：

iris_y_predict=
[2 2 2 2 2 2 2 2 2 2]
iris_y_test
[1 1 1 0 0 0 2 1 2 0]
Accuracy: 0.2
layer nums: 4
1
2
3
4
5
6

扩展内容：

实践1：使用XGB是实现酒店信息消歧

XGB算法是由决策树衍生出来的一种算法。

要求：
酒店的业务人员希望我们能够提供一个算法服务去为酒店信息做一个自动化匹配，以通过算法的手段，找到那些确定相同的酒店和确定不同的酒店

下面按照完整的数据挖掘的步骤进行：
1. 理解业务



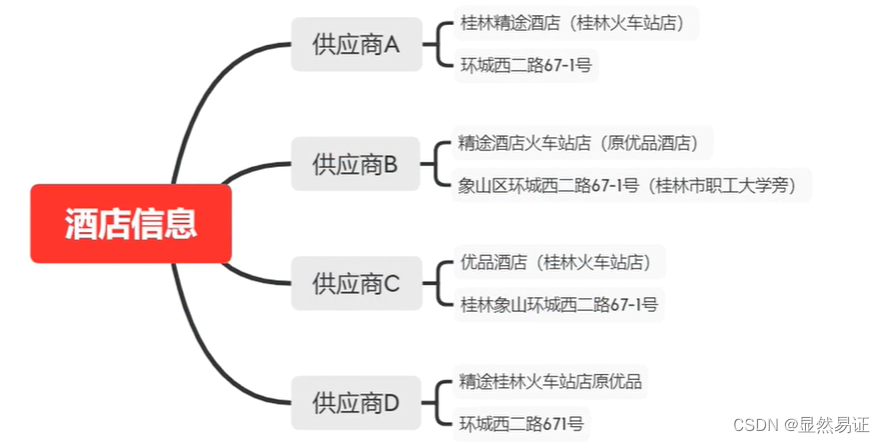
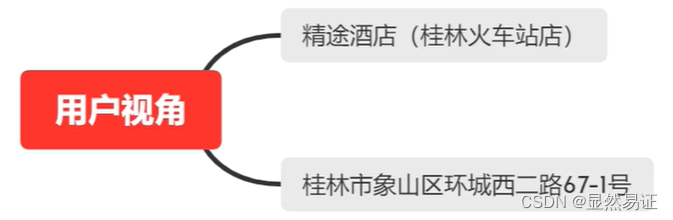
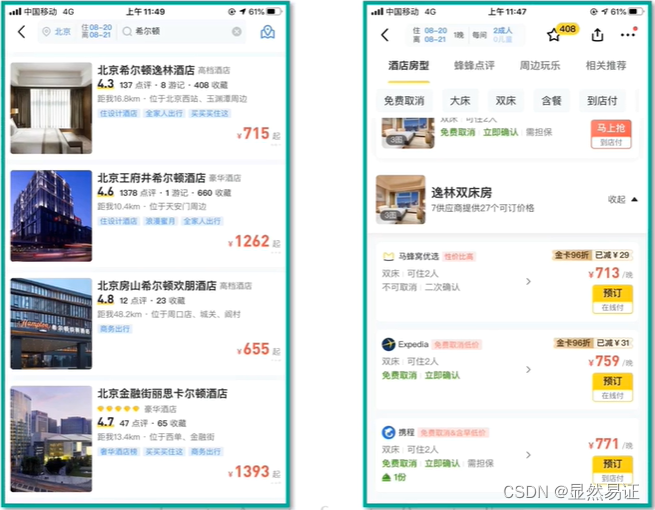
2. 理解数据

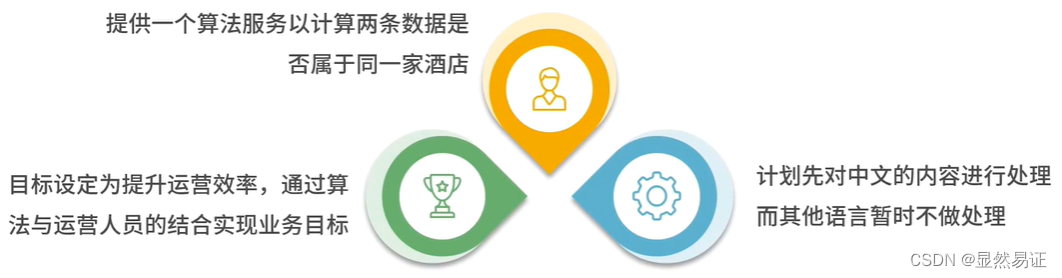
3. 准备数据与模型训练

、

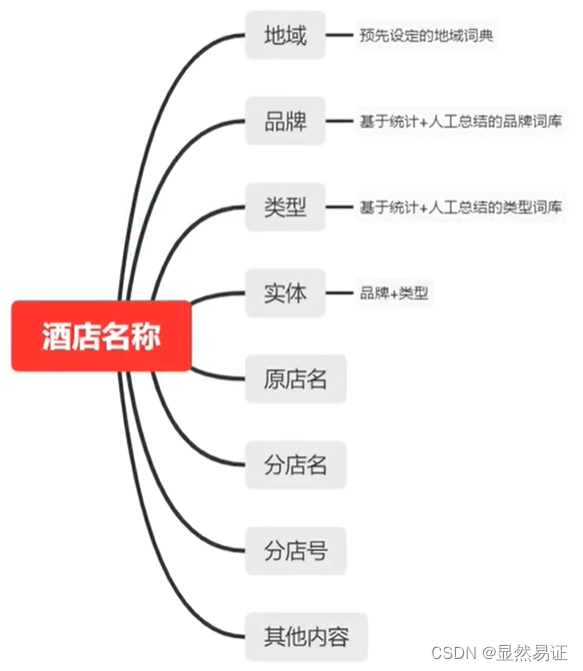
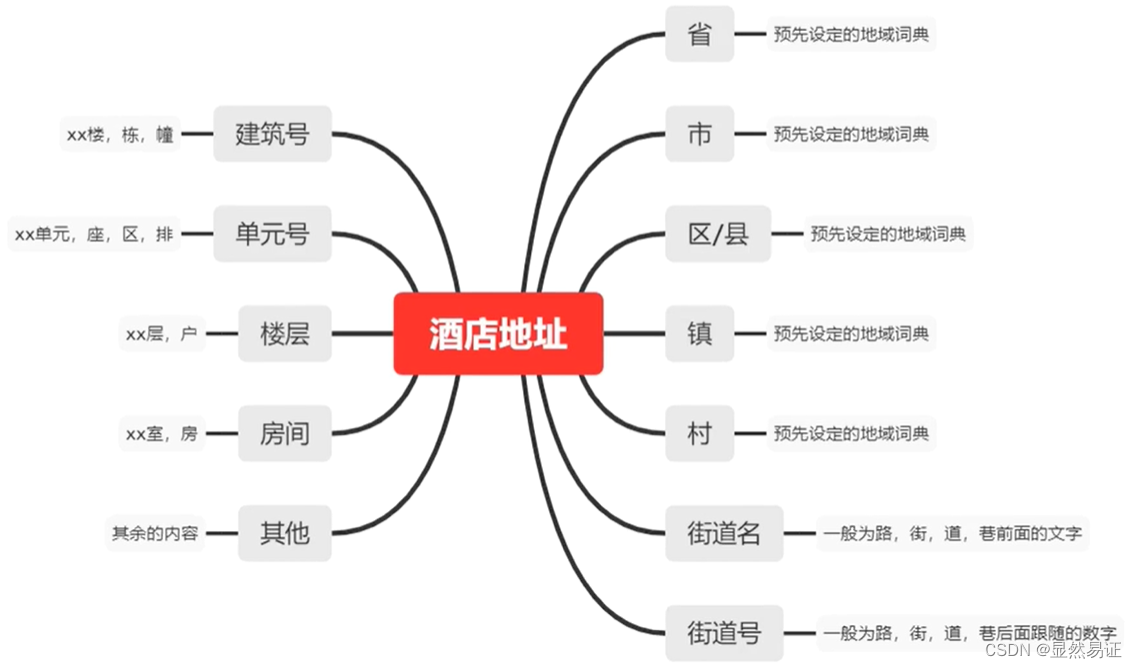
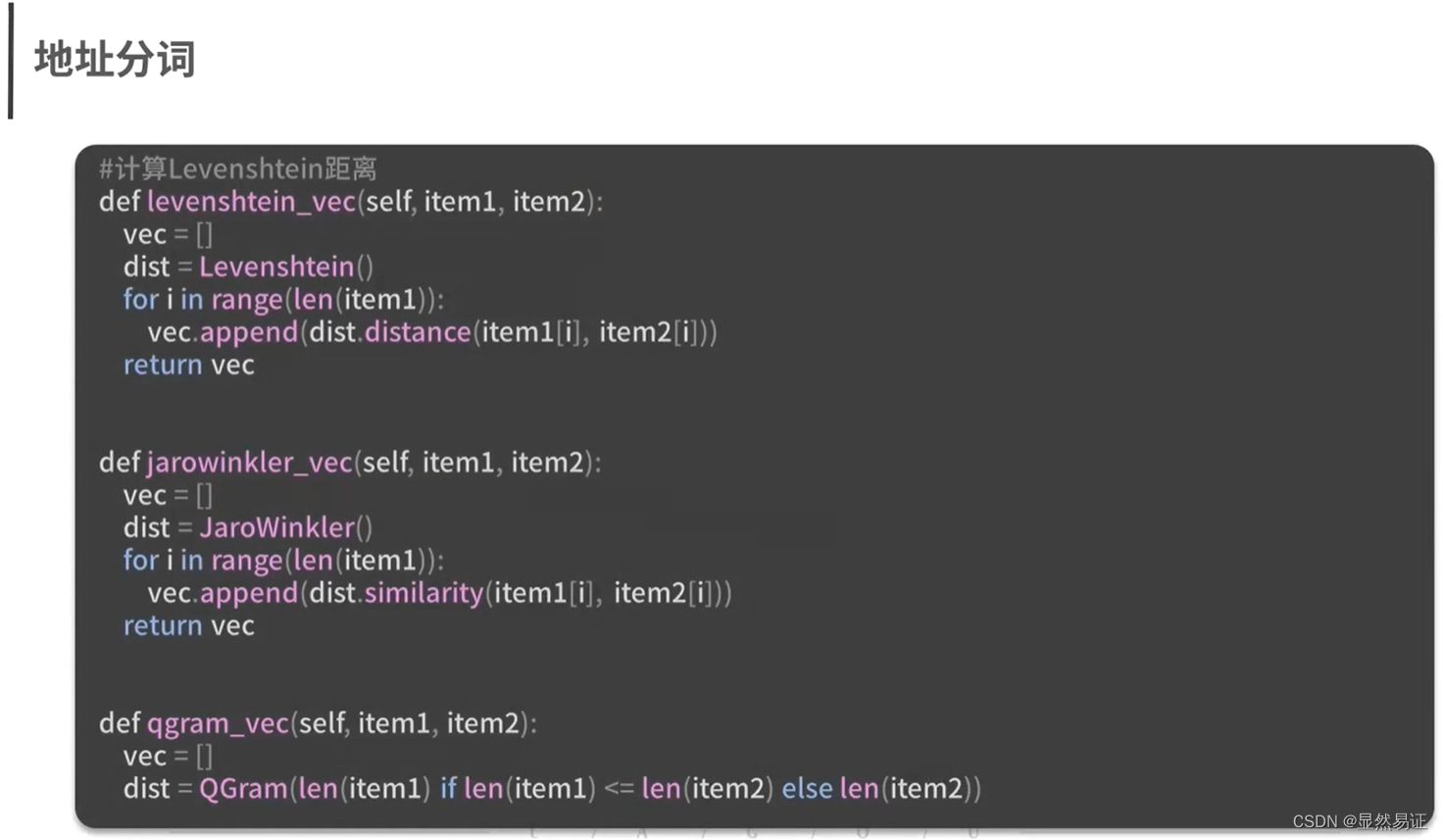
4. 模型训练与评估

聚类算法

K-means

算法内容跳过~~

算法的优点：

1. 简洁明了，计算复杂度低
2. 收敛速度较快

算法的缺点：

1. 结果不稳定
2. 无法解决样本不均衡问题
3. 容易收敛到局部最优解
4. 受噪声影响大

示例代码：

from sklearn import datasets
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np

"""
画出聚类后的图像
labels:聚类后的label，从0开始的数字
cents:质心坐标
n_cluster:聚类后簇的数量
color:每一簇的颜色
"""

def draw_result(train_x, labels, cents, title):
    n_cluster = np.unique(labels).shape[0]
    color = ["red", "orange", "yellow"]
    plt.figure()
    plt.title(title)
    for i in range(n_cluster):
        current_data = train_x[labels == i]
        plt.scatter(current_data[:, 0], current_data[:, 1], c=color[i])
        plt.scatter(cents[i, 0], cents[i, 1], c="blue", marker="*", s=100)
    return plt


if __name__ == '__main__':
    iris = datasets.load_iris()
    iris_x = iris.data
    clf = KMeans(n_clusters=3, max_iter=10, n_init=10, init="k-means++", algorithm="full", tol=1e-4, n_jobs=-1,
                 random_state=1)
    clf.fit(iris_x)
    print("SSE={0}".format(clf.inertia_))
    draw_result(iris_x, clf.labels_, clf.cluster_centers_, "kmeans").show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

代码运行结果：

SSE=78.851441426146
1

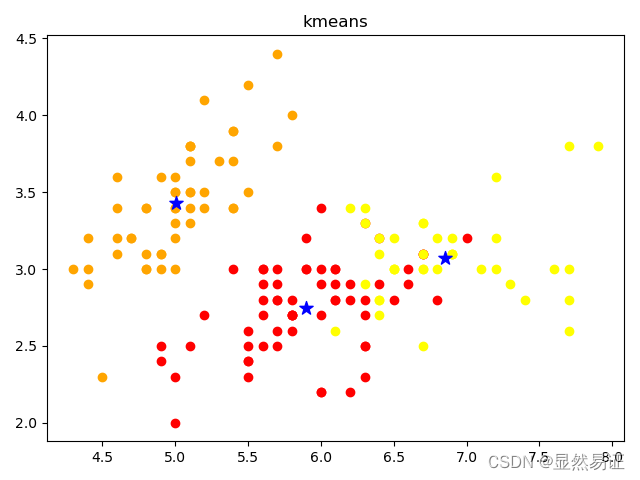
扩展内容：

DBScan

算法内容跳过~~

算法的优点：

1. 不需要划分个数
2. 可以处理噪声点
3. 可以处理任意形状的空间聚类问题

算法的缺点：

1. 需要指定最小样本量和半径两个参数
2. 数据量大时开销很大
3. 样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差

示例代码：

from sklearn import datasets
from sklearn.cluster import dbscan
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

# 生成500个噪声点 噪声为0.1
X, _ = datasets.make_moons(500, noise=0.1, random_state=1)

df = pd.DataFrame(X, columns=['x', 'y'])
df.plot.scatter('x', 'y', s=200, alpha=0.5, c="green", title='dataset by DBSCAN')
plt.show()

# eps为邻域半径，min_samples为最少样本量
core_samples, cluster_ids = dbscan(X, eps=0.2, min_samples=20)
# cluster_ids中-1表示对应的点为噪声
df = pd.DataFrame(np.c_[X, cluster_ids], columns=['x', 'y', 'cluster_id'])
df['cluster_id'] = df['cluster_id'].astype('i2')

# 绘制结果图像
df.plot.scatter('x', 'y', s=200, c=list(df['cluster_id']), cmap='Reds', colorbar=False, alpha=0.6,
                title='DBSCAN cluster result')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

代码运行结果：

扩展内容：

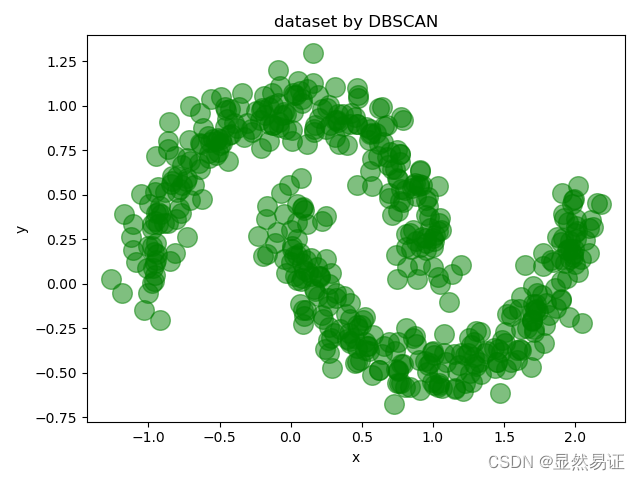
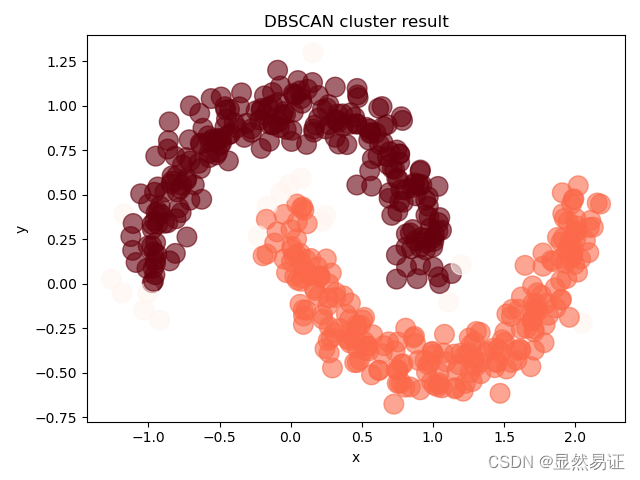
实践2：使用word2vec和k-means聚类

Word2Vec算法：可以学习输入的文本，并输出一个词向量模型

下面按照完整的数据挖掘的步骤进行：
1. 理解业务

2. 理解数据

3.准备数据

4.训练Word2Vec模型

回归算法

线性回归和逻辑回归

算法内容跳过~~

算法的优点：

1. 运算速度快
2. 可解释性强
3. 对线性关系拟合效果好

算法的缺点：

1. 预测的精确度较低
2. 不相关的特征会影响结果
3. 容易出现过拟合

示例代码：

import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import numpy as np


def generateData():
    X = []
    y = []
    for i in range(0, 100):
        tem_x = []
        tem_x.append(i)
        X.append(tem_x)
        tem_y = []
        tem_y.append(i + 2.128 + np.random.uniform(-15, 15))
        y.append(tem_y)
    plt.scatter(X, y, alpha=0.6)
    plt.show()
    return X, y


if __name__ == '__main__':
    np.random.seed(0)
    X, y = generateData()
    print(len(X))
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

    regressor = LinearRegression()
    regressor.fit(X_train, y_train)
    y_result = regressor.predict(X_test)
    plt.plot(X_test, y_result, color='red', alpha=0.6, linewidth=3, label='Predicted Line')
    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

代码运行结果：

100
1

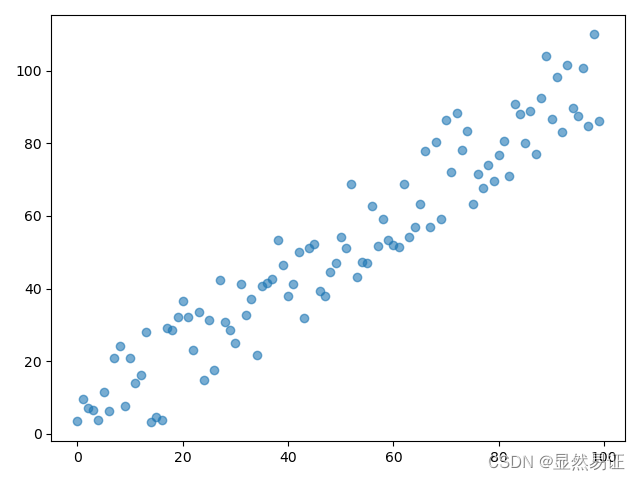
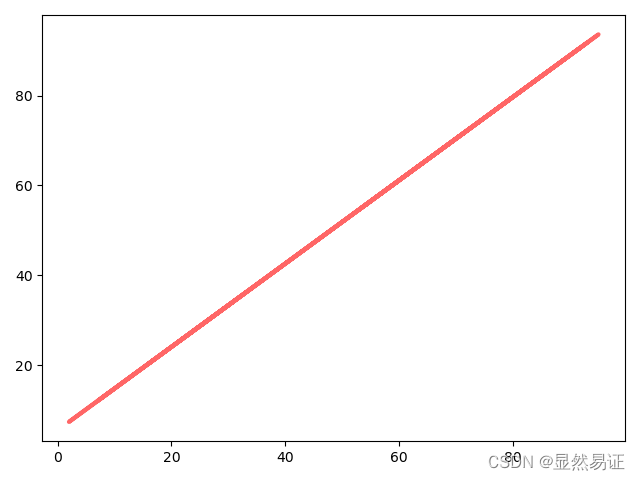
实践3：线性回归预测房价

1. 需求理解、数据理解、数据获取、模型训练
波士顿房价数据集是一个非常常用的公开数据集。
下载两个文件：housing.data是所有的数据、housing.name记录了对数据的介绍


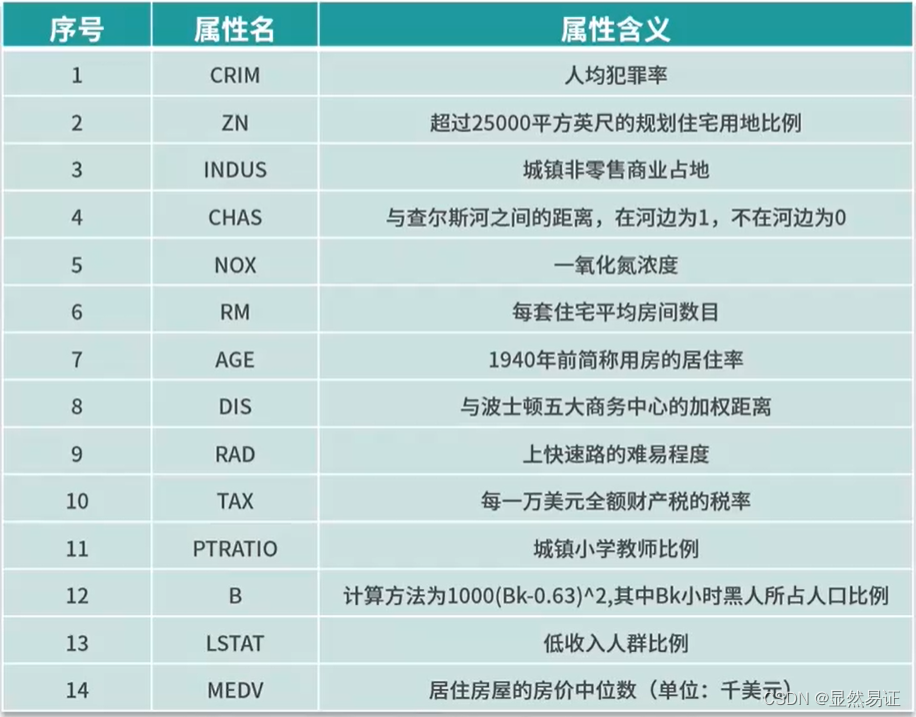
示例代码：

from sklearn.datasets import load_boston
import pandas as pd
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn import metrics
import numpy as np

from sklearn.linear_model import LinearRegression

boston = load_boston()
X = boston.data
y = boston.target
df = pd.DataFrame(X, columns=boston.feature_names)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# 模型训练
regressor = LinearRegression()
regressor.fit(X_train, y_train)

# 查看截距
print(regressor.intercept_)

# 查看斜率
coeff_df = pd.DataFrame(regressor.coef_, df.columns, columns=['Coefficient'])
print(coeff_df)

y_pred = regressor.predict(X_test)
test_df = pd.DataFrame({'Actual': y_test.flatten(), 'Predicted': y_pred.flatten()})
print(test_df)

test_df1 = test_df.head(25)
test_df1.plot(kind='bar', figsize=(16, 10))
plt.grid(which='major', linestyle='-', linewidth=0.5, color='green')
plt.grid(which='minor', linestyle=':', linewidth=0.5, color='black')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

代码运行结果：

38.091694926302125
         Coefficient
CRIM       -0.119443
ZN          0.044780
INDUS       0.005485
CHAS        2.340804
NOX       -16.123604
RM          3.708709
AGE        -0.003121
DIS        -1.386397
RAD         0.244178
TAX        -0.010990
PTRATIO    -1.045921
B           0.008110
LSTAT      -0.492793
     Actual  Predicted
0      22.6  24.889638
1      50.0  23.721411
2      23.0  29.364999
3       8.3  12.122386
4      21.2  21.443823
..      ...        ...
97     24.7  25.442171
98     14.1  15.571783
99     18.7  17.937195
100    28.1  25.305888
101    19.8  22.373233

[102 rows x 2 columns]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

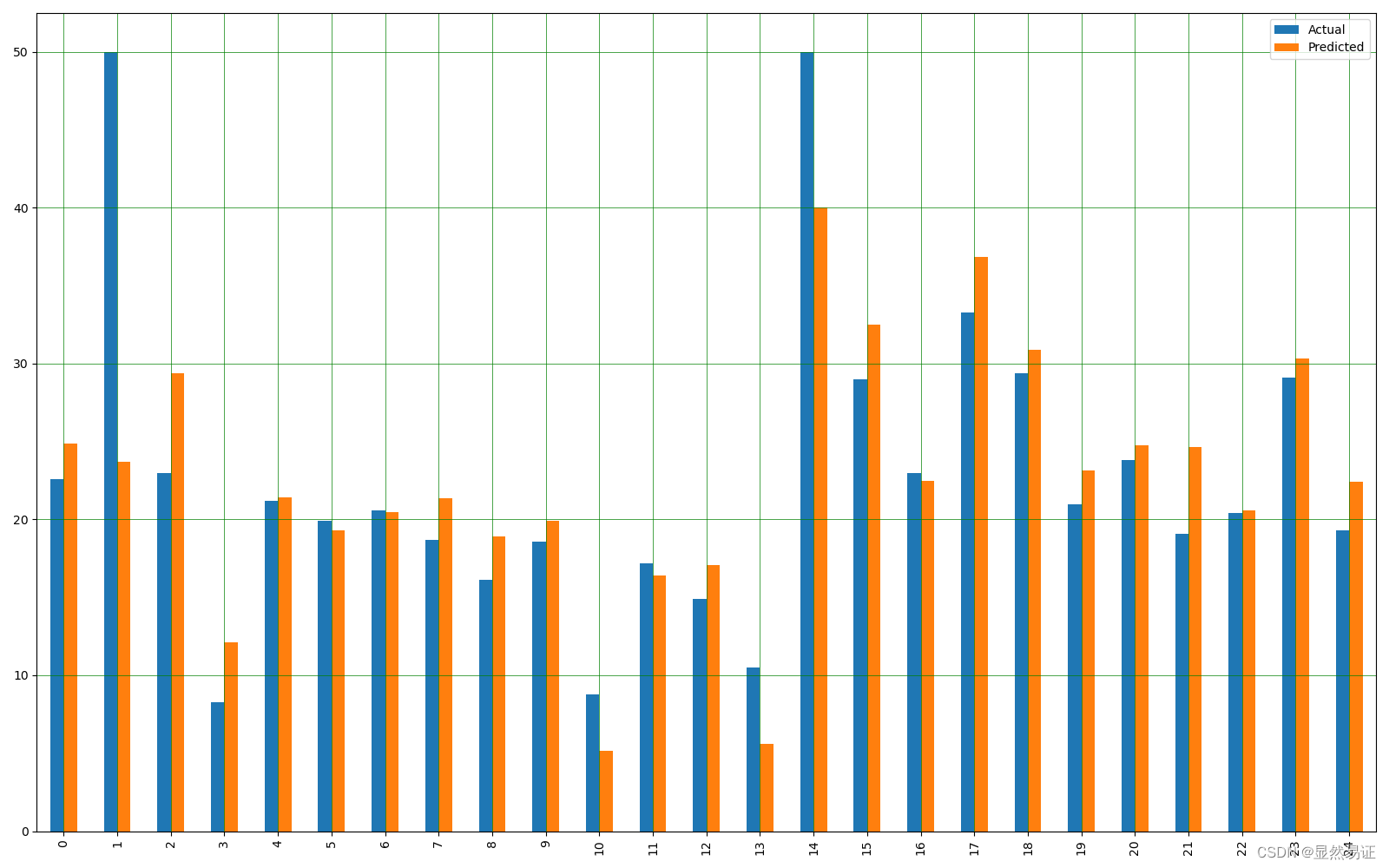
评估：
示例代码：

print('MeanAbsolute Error:', metrics.mean_absolute_error(y_test, y_pred))
print('Mean_squared Error:', metrics.mean_squared_error(y_test, y_pred))
print('RootMean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
1
2
3

评估结果：

MeanAbsolute Error: 3.842909220444496
Mean_squared Error: 33.448979997676474
RootMean Squared Error: 5.78350931508513
1
2
3

关联分析

关联分析是一种无监督学习，目标是从大数据中找出那些经常一起出现的东西。

Apriori与FP-Growth

Apriori算法的核心：如果某个项集是频繁项集，那么其全部子集也都是频繁项集。

算法原理：

1. 找出频繁项集
2. 频繁项集中提取规则

方法论：

1. 假定设定的最小支持度阈值为0.5，那么高于0.5的就认为是频繁项集。
   
   
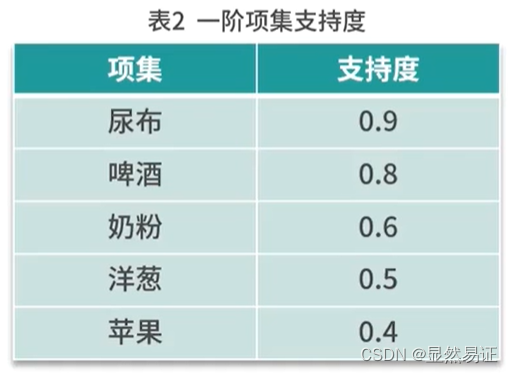
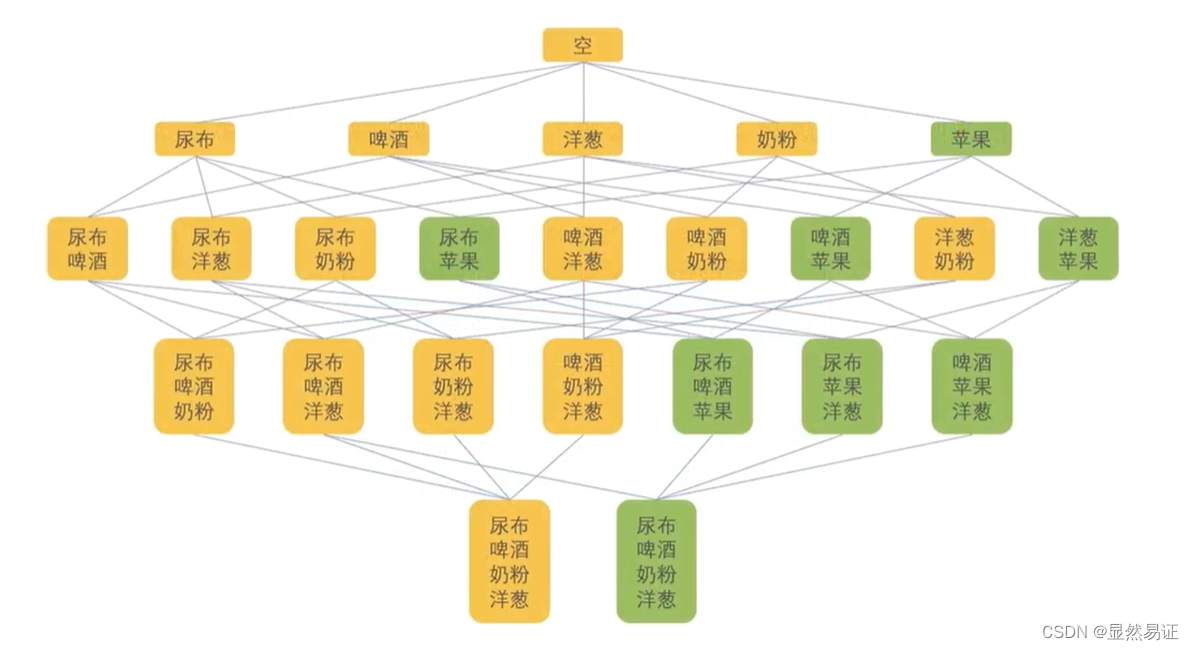
2. 再去计算二阶、三阶…支持度
   
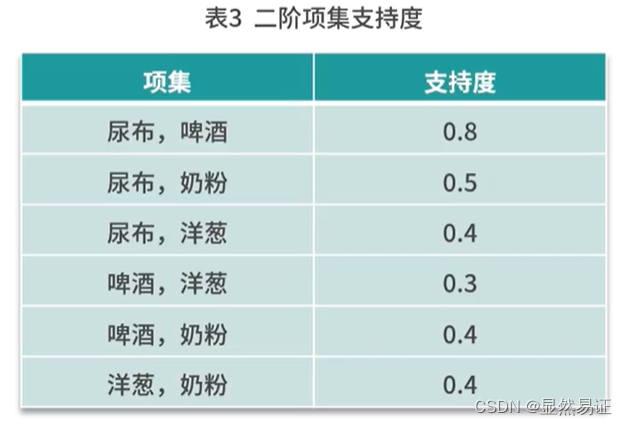
3. 计算三个关联关系的置信度、提升度和确信度
   
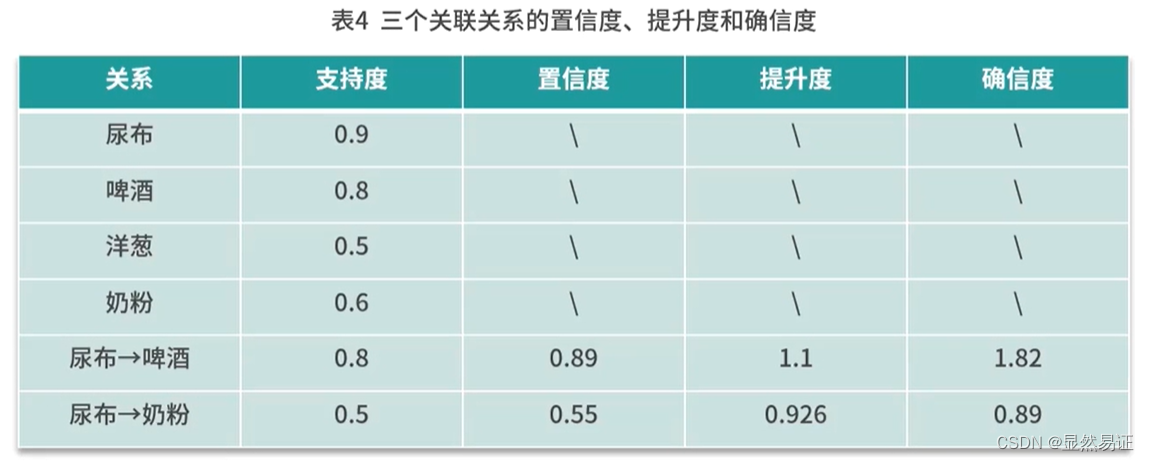
4. FP-Growth(Frequent Pattern Growth)
   
   

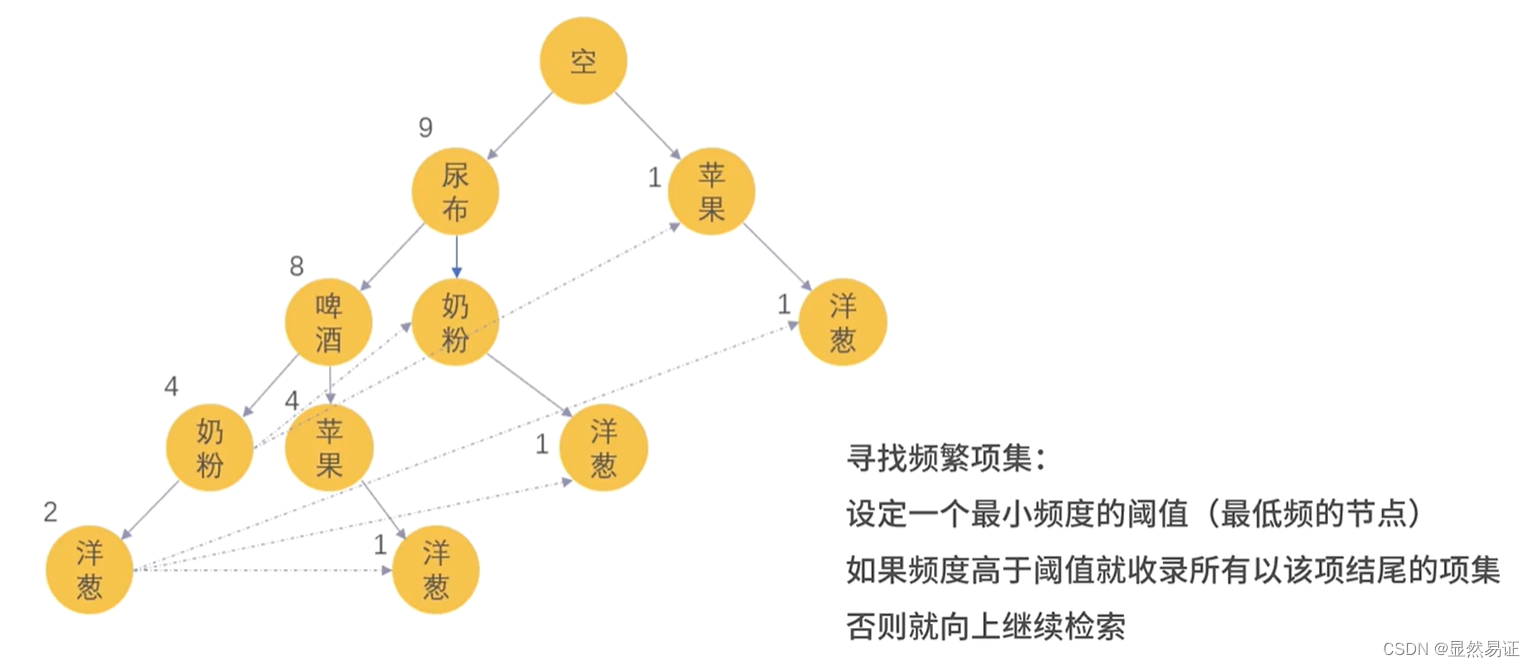
示例代码：

from efficient_apriori import apriori

data = [('尿布', '啤酒', '奶粉', '洋葱'),
        ('尿布', '啤酒', '奶粉', '洋葱'),
        ('尿布', '啤酒', '苹果', '洋葱'),
        ('尿布', '啤酒', '苹果'),
        ('尿布', '啤酒', '奶粉'),
        ('尿布', '啤酒', '奶粉'),
        ('尿布', '啤酒', '苹果'),
        ('尿布', '啤酒', '苹果'),
        ('尿布', '奶粉', '洋葱'),
        ('奶粉', '洋葱')]

itemsets,rules = apriori(data,min_support=0.4,min_confidence=1)
print(itemsets)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

代码运行结果：

{1: {('尿布',): 9, ('啤酒',): 8, ('奶粉',): 6, ('洋葱',): 5, ('苹果',): 4}, 2: {('啤酒', '奶粉'): 4, ('啤酒', '尿布'): 8, ('啤酒', '苹果'): 4, ('奶粉', '尿布'): 5, ('奶粉', '洋葱'): 4, ('尿布', '洋葱'): 4, ('尿布', '苹果'): 4}, 3: {('啤酒', '奶粉', '尿布'): 4, ('啤酒', '尿布', '苹果'): 4}}
1

总结：
Apriori算法：使用的穷举的当时
FP-Growth算法：使用了树形结构来提高速度

不管是使用什么算法来挖掘的关联关系，都可以使用关联关系的评估指标来进行评估