Machine learning week 10(Andrew Ng)

Reinforcement learning

1. Reinforcement learning introduction

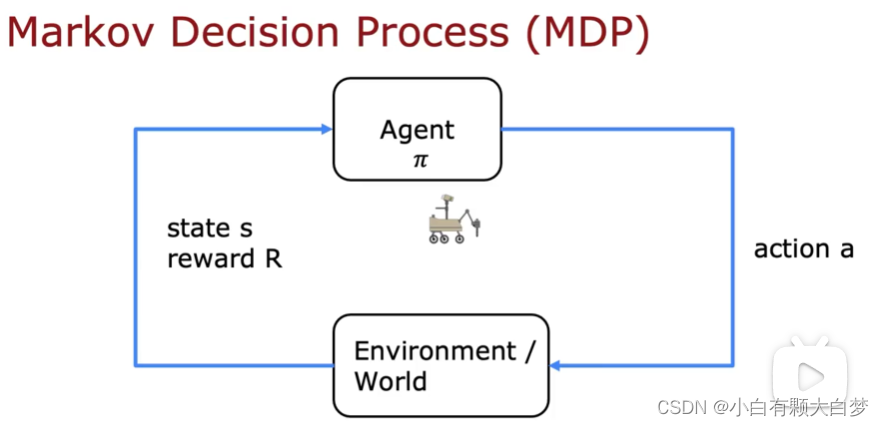
1.1. What is Reinforcement Learning?

The key idea is rather than you need to tell the algorithm what the right output y for every single input is, all you have to do instead is specify a reward function that tells it when it’s doing well and when it’s doing poorly.

1.2. Mars rover example

1.3. The return in Reinforcement learning

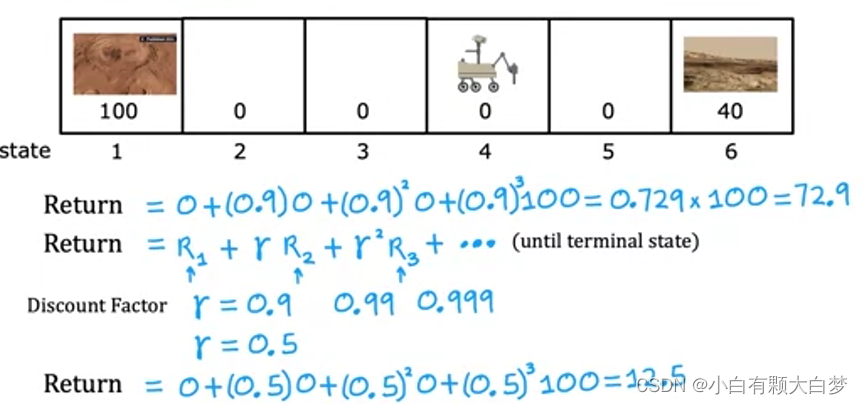
The first step is $r^0$.

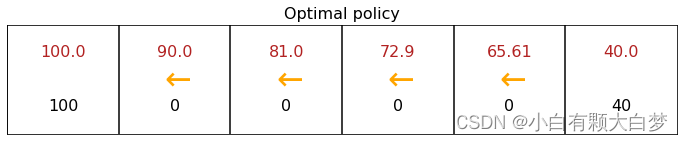
Select the orientation according to the first two tables

1.4. Making decisions: Policies in reinforcement learning

For example, $\pi (2)$ is left while $\pi (5)$ is right. The number expresses state.

1.5. Review of key concepts

2. State-action value function

2.1. State-action value function definition

The iteration will be used.

2.2. State-action value function example

2.3. Bellman Equation

$$Q(s,a)=R(s)+r\ast maxQ(s^{{}^{\prime }},a^{{}^{\prime }})$$

2.4. Random (stochastic) environment

Sometimes it actually ends up accidentally slipping and going in the opposite direction.

3. Continuous state spaces

3.1. Example of continuous state space applications

Every variable is continuous.

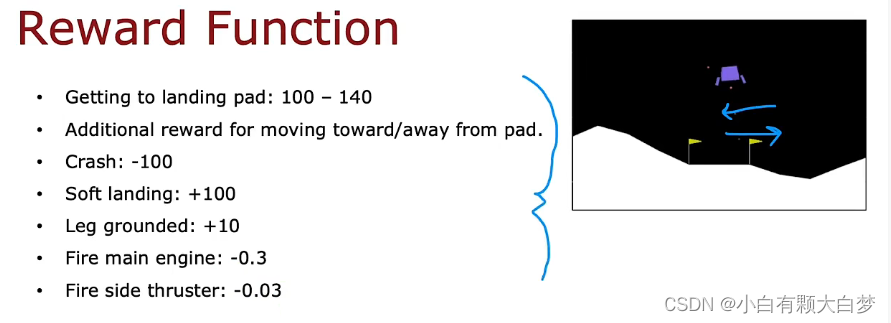
3.2. Lunar lander

3.3. Learning the state-value function

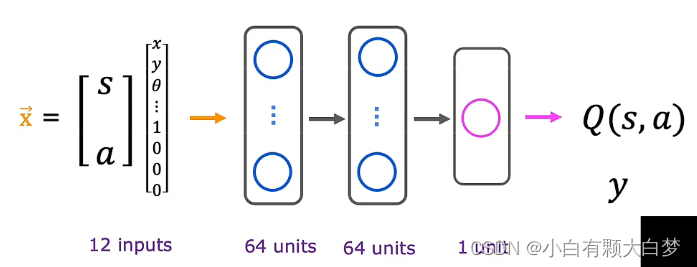
Q is a random value at first. We will train the model to find a better Q.

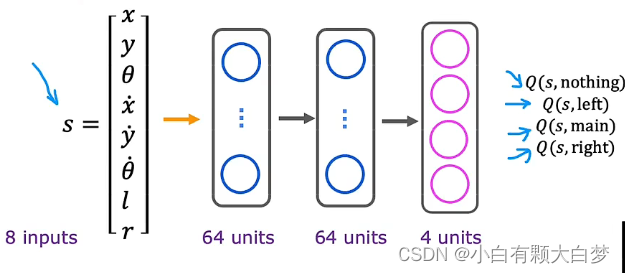
3.4. Algorithm refinement: Improved neural network architecture

3.5. Algorithm refinement: ε-greedy policy

ε = 0.05

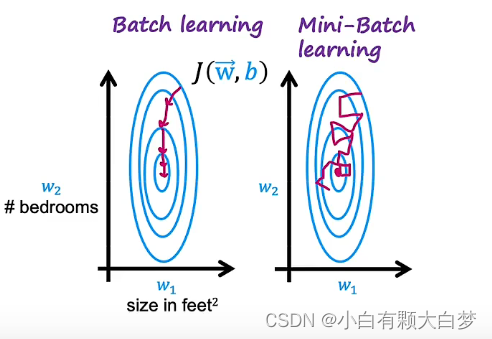
If we choose a bad ε, we may take 100 times as long.

3.6. Algorithm refinement: Mini-batch and soft update

The idea of mini-batch gradient descent is to not use all 100 million training examples on every single iteration through this loop. Instead, we may pick a smaller number, let me call it m prime equals say, 1,000. On every step, instead of using all 100 million examples, we would pick some subset of 1,000 or m prime examples.

• Soft update
  When we set Q equals to $Q_{new}$, it can make a very abrupt change to Q.So we will adjust the parameters in Q.
  $W=0.01\ast W_{new}+0.99W$
  $B=0.01\ast B_{new}+0.99B$

3.7. The state of reinforcement learning

Summary