基于贝塞尔曲线（Bézier Curve）与硬约束的轨迹优化方法

0 思想

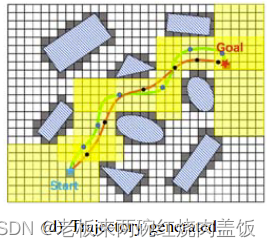
这个方法参考的是高老师的一篇论文，注意下方图片的黄色区域，这个方法的思想就是，这个黄色区域是与障碍物没有碰撞的，假设我们能把我们的轨迹约束在这些区域里，那么我们肯定也能找到一条没有碰撞的曲线。

---

---

但是呢，之前我们选择的曲线表达式，也就是在$Minimum$ $Snap$当中使用的多项式曲线表达式，如下所示：

p μ ( t ) = { ∑ j = 0 N η 1 j ( t − T 0 ) j T 0 ≤ t ≤ T 1 ∑ j = 0 N η 2 j ( t − T 1 ) j T 1 ≤ t ≤ T 2 ⋮ ⋮ ∑ j = 0 N η M j ( t − T M − 1 ) j T M − 1 ≤ t ≤ T M p_{\mu}(t)=\left\{

\right. pμ​(t)=⎩ ⎨ ⎧​∑j=0N​η1j​(t−T0​)j∑j=0N​η2j​(t−T1​)j⋮∑j=0N​ηMj​(t−TM−1​)j​T0​≤t≤T1​T1​≤t≤T2​⋮TM−1​≤t≤TM​​

将这种多项式的曲线约束在黄色的约束里面是非常麻烦的，所以想到了用另外一种曲线来代替，这边使用的是贝塞尔曲线。

1 贝塞尔曲线（Bézier Curve）

---

---

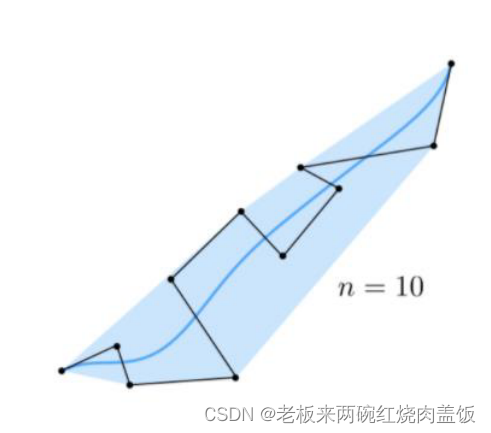
这条贝塞尔曲线是在蓝色的凸多边形里面，贝塞尔曲线有一个凸包特性，这个曲线会在一个凸包里面，假设这个凸包是在上方黄色的安全区域里面，那么就可以把轨迹约束在安全区域里面了。

1.1 贝塞尔曲线的构造

$${\mathbf{b}}^n(t)={\mathbf{b}}_0^n(t)=\sum _{j=0}^n{\mathbf{b}}_j{B}_j^n(t)$$

可以看出，这个$b_j$就是控制点，对应的是上图当中的小黑点，$n=10$表示贝塞尔曲线的阶数，$10$阶是最高的阶数了，$10$阶的贝塞尔曲线是有$11$个控制点的，假设有$m$个控制点，其阶数就是$n-1$的。$b_j$即为控制点，$B_j$即为伯恩斯坦多项式（$n$次的标量多项式）

构造步骤：可以看看大佬的Blog

---

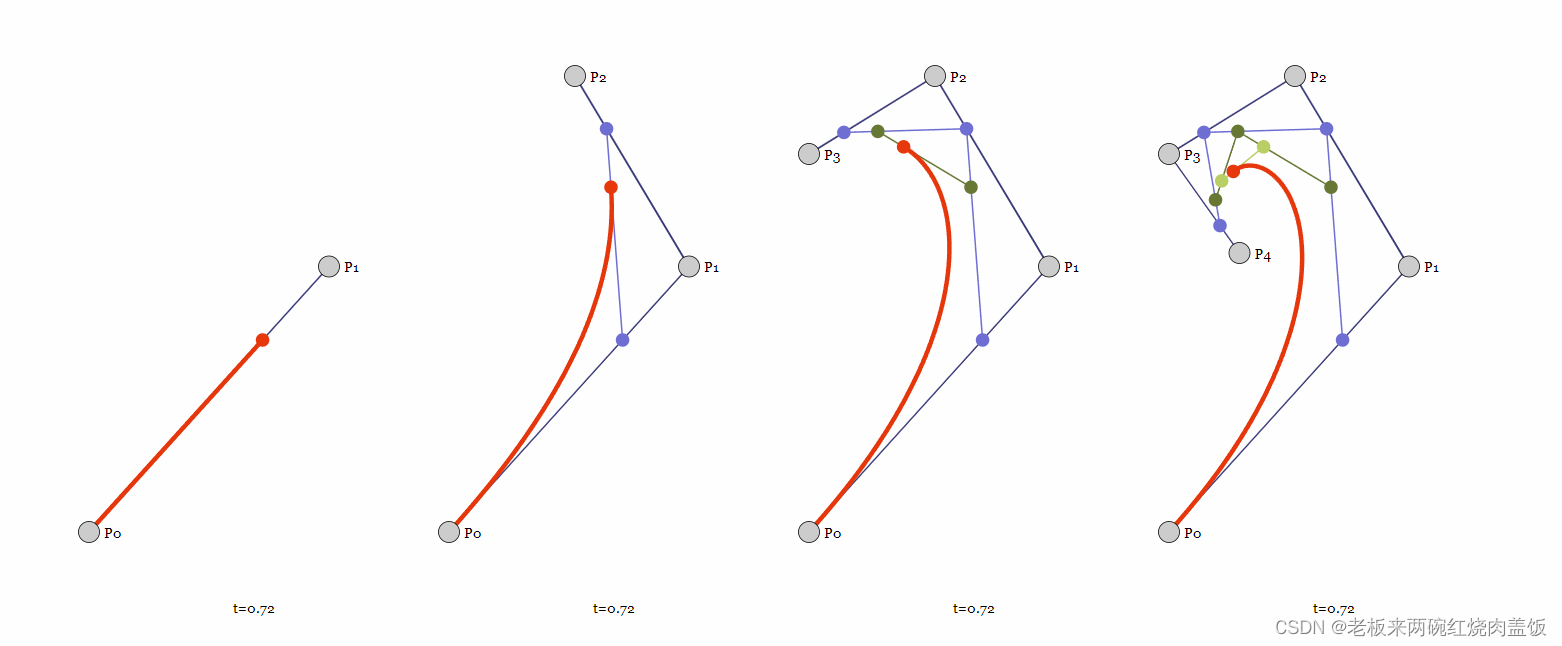
可以看出贝塞尔曲线的凸包特性。

---

贝塞尔曲线方程完全展开：
B i n ( t ) = ( n i ) t i ( 1 − t ) n − i B_i^n(t)=\left(

\right) t^i(1-t)^{n-i} Bin​(t)=(ni​)ti(1−t)n−i
$n、i$就是组合的表达形式，二次项的形式。

1.2 贝塞尔曲线的转化

上述已经说了，又变成了二次项的形式，
b 0 1 ( t ) = ( 1 − t ) b 0 + t b 1 b 1 1 ( t ) = ( 1 − t ) b 1 + t b 2 b 0 2 ( t ) = ( 1 − t ) b 0 1 + t b 1 1 b 0 2 ( t ) = ( 1 − t ) 2 b 0 + 2 t ( 1 − t ) b 1 + t 2 b 2

b01​(t)b11​(t)b02​(t)b02​(t)=(1−t)2b0​+2t(1−t)b1​+t2b2​​=(1−t)b0​+tb1​=(1−t)b1​+tb2​=(1−t)b01​+tb11​​

所以，就可以将原先的多项式曲线表达形式，进行贝塞尔曲线的转化，就是把多项式曲线，重新展开，再进行排列，又回到了多项式的形式，所以，贝塞尔曲线就是一种特殊的多项式曲线。

所以，成为多项式曲线，之前在$Minimum$ $Snap$中的方法又可以拿起来使用了。优化过程就可以转变成$Minimum$ $Snap$那种形式。

---

这是一个6阶的贝塞尔曲线转换的情况，以上为转换的映射矩阵。

---

1.3 飞行走廊（黄色安全区域的构建）

---

每一个栅格保存了距离最近的障碍物，红线的路径假设是A*算法求出来的，红色虚线路径上的小点，地图上保存了距离这个点最近的障碍物的距离，这样在二维上可以画出圆，表示安全的范围，这个球还是可以扩展，形成一个大范围的安全区域，可以在圆里找到内接的矩阵/正方形，这些还是可以扩展一些。

---

如下是扩展完成的图。

---

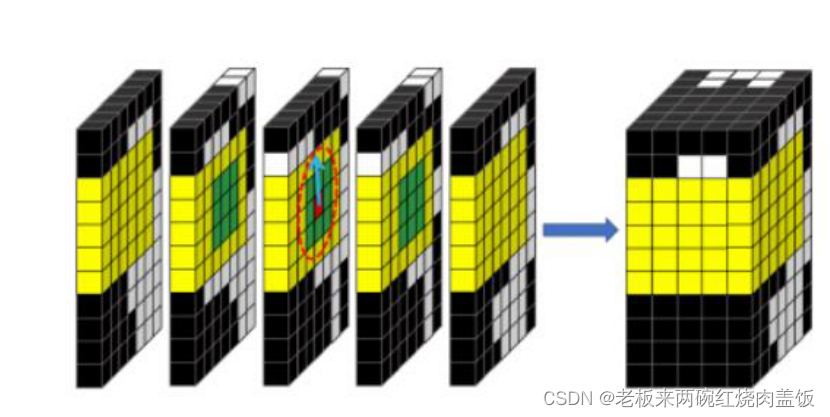
这样就是有很多长方体（三维），贝塞尔曲线就约束在长方体里面，就肯定是安全区域。
一个性质，贝塞尔曲线的导数仍然是贝塞尔曲线。

2 总结

一个多项式，转换为贝塞尔曲线，然后继续使用$Minimum$ $Snap$的方法去优化。