【软考学习6】计算机存储结构——局部性原理、Cache、主存地址单元、磁盘存取、总线和可靠性

---

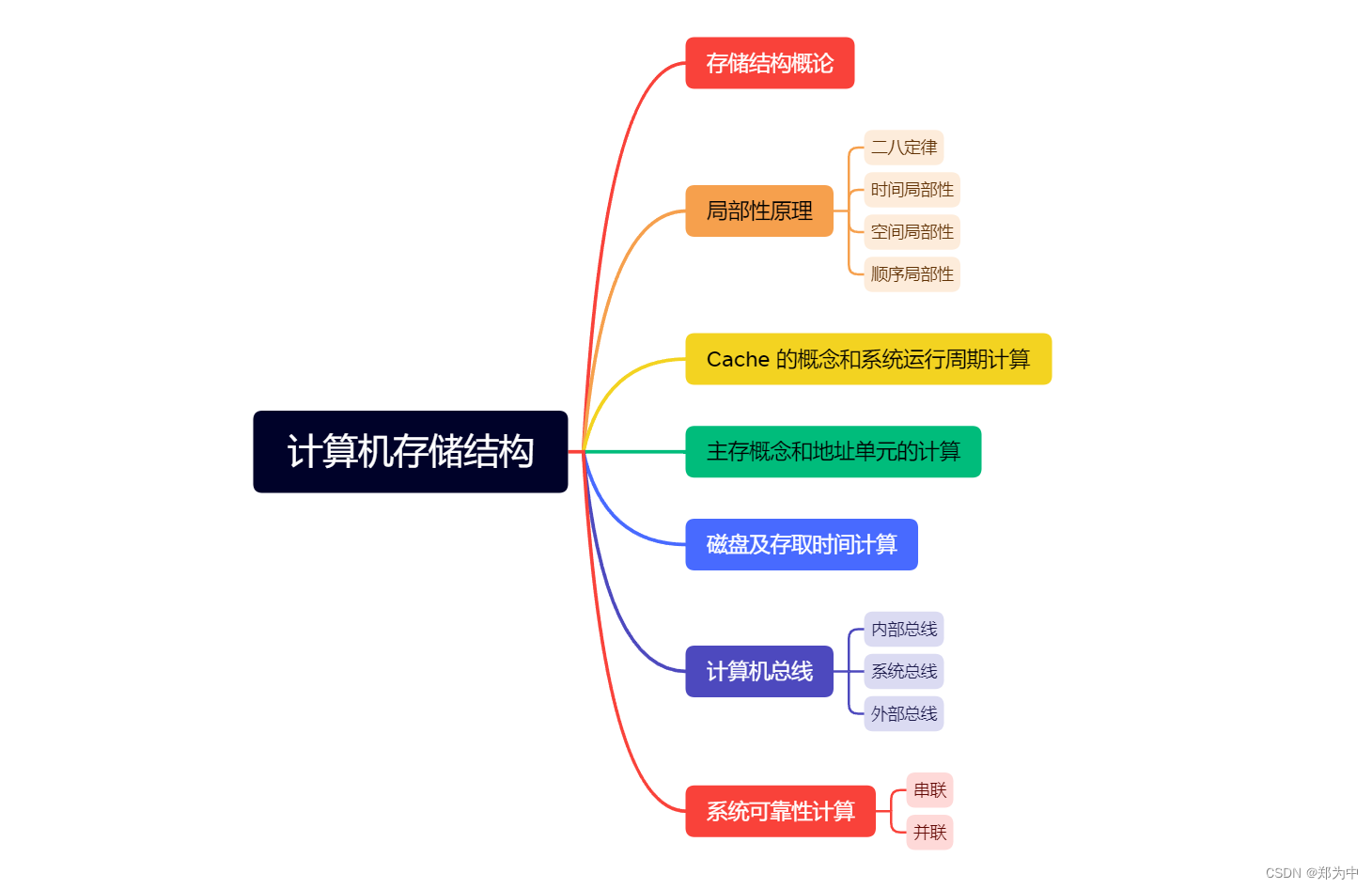
一、存储结构概论

计算机的存储机构包括了 CPU 的 寄存器，用于临时缓存指令数据，还有 高速缓存 Cache、内存 和 外存，如下图所示。

---

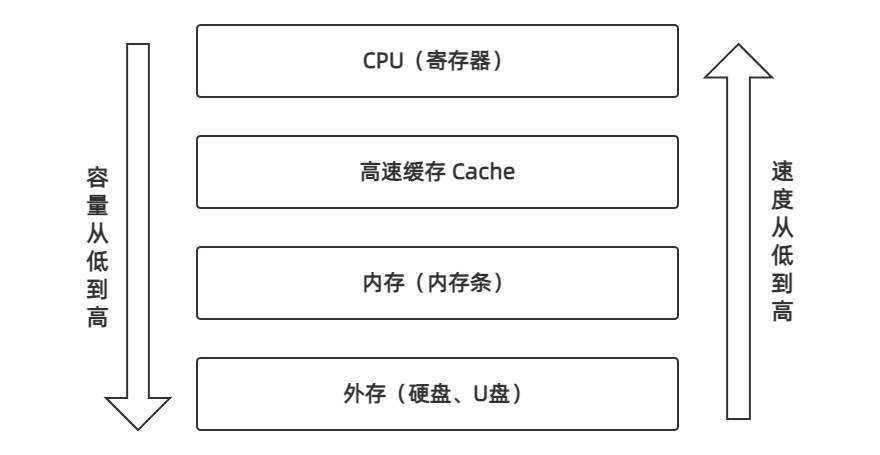
• 寄存器：CPU 的寄存器一般在运算器和控制器中，作为一个临时缓存，一般的寄存器存储容量只有 1 - 64 KB 个大小。
• 高速缓存：又称 Cache，速度位于寄存器和内存之间，CPU 的寄存器在取指令操作时，先到 Cache 中查询，若有则直接返回，若没有才会到内存中读取，Cache 的存在可以加快 CPU 的执行效率，一般以 MB 作为计量单位。
• 内存：是计算机的运行内存，现代计算机的内存容量一般在 4G - 32G 范围内。
• 外存：是计算机系统的外部存储设备，如硬盘、U 盘等，现代外存的容量一般以 TB 作为计算单位。

---

二、局部性原理（Cache 的使用场景）

首先我们了解一下 二八定律，和我们即将学习的局部性原理很类似。

帕累托法则又称二八定律，是一种量化的实证法，用以计量投入和产出之间可能存在的关系。
该定律的内容指出：20％的人口掌握了80％的社会财富，这个结论对大多数国家的社会财富分配情况都成立。因此，该法则又被称为80/20法则。

举个例子：

假如20%购车的人买掉了80%的汽车，那么这部分人应该是汽车厂商注意的对象。

尽可能争取这20%的人来买，最好能进一步增加他们的购车消费。

汽车制造商出于实际理由，可能会忽视其余80%购车的人，因为他们的消费量只占20%。

---

2.1 时间局部性

对于计算机编程来说，循环执行 是再也正常不过的事情了，如下面的代码所示。

public static void main(String[] args) {
    Integer sum = 0;
    for(int i = 1; i <= 100; i ++) {
        sum += i;
    }
    System.out.println(sum);
}
1
2
3
4
5
6
7

要计算 1 到 100 的累加和，如果不用高斯定理，就只能这么循环去累加计算。

对于代码来讲，其实也就 7 行代码，但是对于计算机来说，sum += i; 这行程序要执行 100 次，而 Integer sum = 0; 这一初始化程序只会被执行一次，这就是 时间局部性 。

时间局部性：如果一个信息项正在被访问，那么在近期它很可能还会被再次访问。

不仅仅是对于循环语句，对于堆栈类的程序也一样适用，比如 DFS 深搜。

---

2.2 空间局部性

空间局部性一般存在于 数组 之上，比如我们需要对一个数组进行初始化，代码如下所示。

public static void main(String[] args) {
    Integer[] array = new Integer[100];
    for(int i = 0; i < 100; i ++) {
        array[i] = i;
    }
    System.out.println("Init Finish!");
}
1
2
3
4
5
6
7

首先创建 array 数组对象后，拿到了对象的首地址。

接着对 array[0]赋值的时候，就是对 array对象的首地址赋值。

接着对 array[1]赋值的时候，就是对 array对象后的 4 个地址（Integer的占位大小）赋值。

接着对 array[2]赋值的时候，就是对 array对象后的 8 个地址（Integer的占位大小 * 2）赋值。

以此类推，每给 array[n] 赋值。就要进行 4 * n 顺序遍历，才能成功赋值。

如果有一个缓存去临时存储当前的地址，是不是可以解决重复遍历的问题？

---

2.3 顺序局部性

当然还有一个 顺序局部性 的概念，在典型程序中，除转移类指令外，大部分指令是顺序进行的。顺序执行和非顺序执行的比例大致是5:1。此外，对大型数组访问也是顺序的。

指令的顺序执行、数组的连续存放等是产生顺序局部性的原因。

---

三、Cache 的概念和系统运行周期计算

Cache 存在的意义，就是提高 CPU 输入输出的速度，突破 CPU 和内存之间的存储上限。

因为计算机 局部性原理 的存在，所以 Cache 的投入使用可以大大提高计算机的运行速度。

简单来说，根据 局部性原理 和 二八定律，将 20% 常用的指令放在 Cache 中，可以达到加速 80%的效果。

软考中对于 Cache 的考察有一类计算题，就是根据 Cache 的命中率，计算系统运行周期。

假设 Cache 的命中率为 X，不用 Cache （没有命中）的周期时间为 A，用了 Cache（命中）的周期时间为 B，那么使用 Cache + 内存模式 的系统平均周期为多少？

计算公式： 系统平均周期 = X * A + （1 - X）* B。

如：假设 Cache 的命中率为 95%，不用 Cache （没有命中）的周期时间为 50 纳秒，用了 Cache（命中）的周期时间为 9 纳秒，那么使用 Cache + 内存模式 的系统平均周期为多少？

系统平均周期 = 95% * 9 + （1- 95%） * 50 = 8.55 + 2.5 = 11.05（纳秒）。

---

四、主存概念和地址单元的计算

主存可分为两类，分别是 随机存取存储器 和 只读存储器。

随机存取存储器 还可以分为静态和动态，静态的是 SRAM，动态的是 DRAM。

只读存储器 包括磁盘，但不包括固态硬盘。

---

在主存模块中，会考察到地址单元的计算，公式如下。

地址单元 = 尾地址 - 首地址 + 1

比如内存首地址为 2，尾地址为 18，那么这块内存包含了 18 - 2 + 1 = 17个地址单元。

但题目一般都是十六进制，比如 内存地址从 BA235H 到 BC954H，求共有多少个地址单元。

首先对首位地址进行十六进制减法。

 BC954H
-BA235H
-------
=02719H
1
2
3
4

再将 02719H 转为十进制。

(9 x 16^0) + (1 x 16^ 1) + (7 x 16^ 2) + (2 x 16^3) = 9 + 16 + 1792 + 8192 = 10009
1

答案就是一共有 10009 个地址单元。

第二问，如果该内存一共有 1000K 个地址单元，按字节编址（16位），由 28 片存储器芯片构成，已知每片芯片有 36K 个，则每块芯片的每个存储单元存储几位？

计算公式如下：

1000K * 16 = 28 * 36K * 存储单元位数
即 存储单元位数 = 28 * 36K / 16 / 1000K
1
2

---

五、磁盘及存取时间计算

磁盘的物理构成如下图所示。

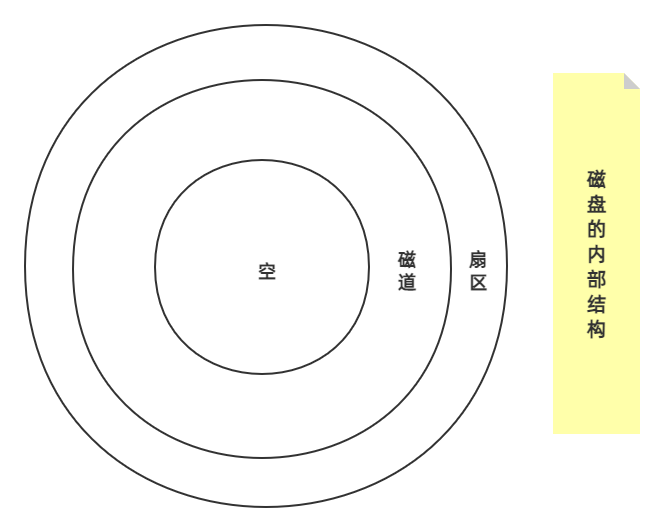
在对磁盘的数据进行一次存储时，需要消耗一定的时间，我们称为 磁盘存取时间。

这个 磁盘存取时间 可分为两部分，一个是 寻道时间，还有一个是 等待时间。

在 360° 的磁道上，必定有一个 磁头，可以理解为一个数组的首元素指针。

寻道时间 指的是磁头移动到磁道所需的时间，我们设为 X。

等待时间 指的是等待扇区转到磁道所用的时间，我们设为 Y。

接下来以一个实际例题来演示。

---

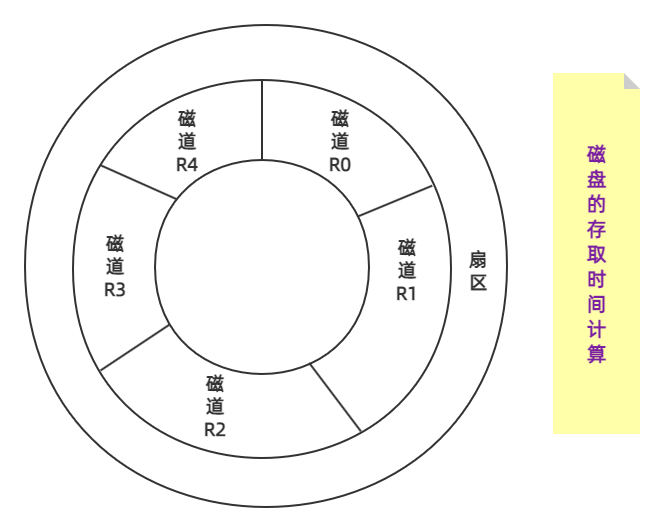
题目：
如果磁盘的旋转周期为 25 毫秒，磁头处于 R0 的开始处。若系统采用单缓冲区处理这些记录，每个记录的处理时间为 6 毫秒，则处理这
5 个记录的最长时间为多少毫秒？

---

磁盘的旋转周期为 25 毫秒，磁道一共分为 5 块，所以得出每个单位的磁道旋转读取需要消耗 5 毫秒时间。

首先 磁头从 R0 开始，读取 R0 的数据需要 5 毫秒，接着磁头移动到 R1 的开始处，如下图所示。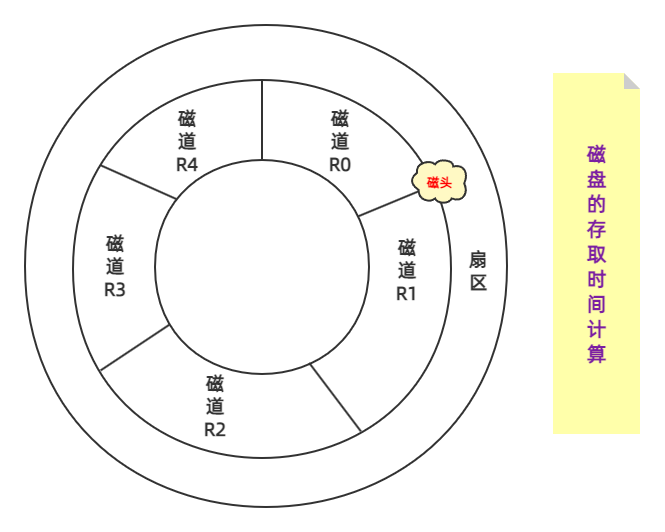

此时需要处理磁道 R0 的数据，处理的时间为 6 毫秒，磁盘开始处理 R0 的数据，但磁头继续移动（不会停），等磁盘处理好 R0 的数据后，磁头移动情况如下图所示。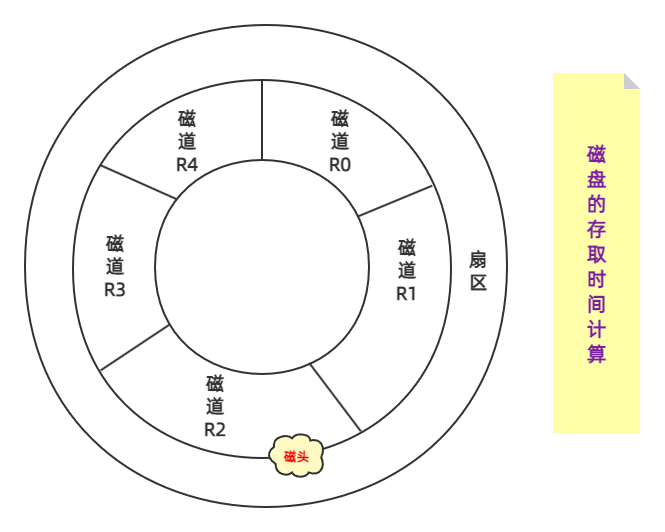

磁盘接着要处理 R1 的数据，但磁头已经超过了 R1，无法读取，只能等磁头再转一圈，这就叫“过犹不及”！

等磁头再次转到 R1 起始位置时，消耗的时间为读取 R0 的 5 毫秒 + 处理 R0 的 6 毫秒 + 磁头从上图到 R1 起始处的时间，即 5 + 6 + 19，等于30 毫秒，接着磁头又到了如下图所示的位置。

接着对于 R1 以此类推，读取需要 5 毫秒（25 的旋转周期分 5 份），处理需要 6 毫秒，处理后磁头位置如下图所示。

同理可得完成 R1 处理的时间同 R0，也是 30 纳秒， R0 到 R4 都是这样。

所以最终的存取时间等于 30 x 5 = 150 毫秒。

---

六、计算机总线

计算机总线的分类，如下图所示。

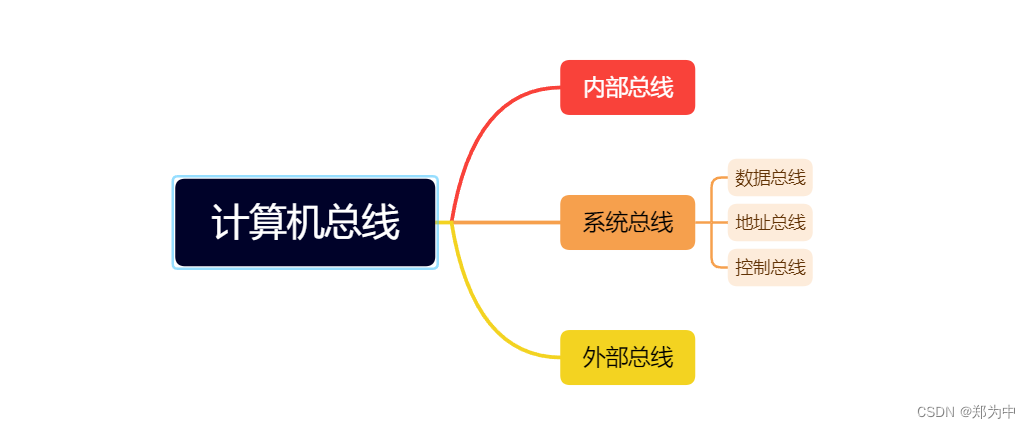
• 内部总线：寄存器和寄存器之间的连接、芯片内部的连接、寄存器和运算器 / 控制器之间的连接。
• 系统总线：CPU、内存之间的连接。
• 外部总线：主机和鼠标、键盘、麦克风等外部设备的连接。

---

其中系统总线中的分为数据总线、地址总线和控制总线，它们的功能分别如下所示。

数据总线：双向传输，和机器字长、存储字长有关。
地址总线：单向传输，和存储地址、I/O地址有关。
控制总线：用于发出信号（存储器读、存储器写、总线允许、中断确认等操作）；接收信号（中断请求、总线请求等操作）

---

七、系统可靠性计算

系统可靠性需要区分 串联 和 并联，对于两者有不同的计算公式。

串联

串联 的情况如下图所示，分系统 R1、R2、R3 和 R4 用串联的方式连接。

假设系统 R1 的可靠性为 A1，设系统 R2 的可靠性为 A2，设系统 R3 的可靠性为 A3，设系统 R4 的可靠性为 A4。

这个串联系统的可靠性为 R1 x R2 x R3 x R4。

计算公式为： R1 x R2 x … x Rn。

误差率计算公式为：（1 - R1）x（1 - R2）x … x（1 - Rn），仅供参考，误差率较大。

---

并联

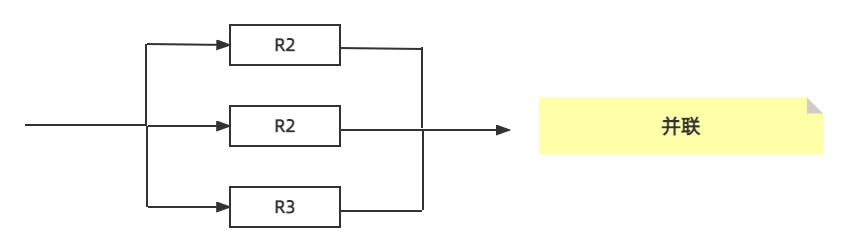
假设系统 R1 的可靠性为 A1，设系统 R2 的可靠性为 A2，设系统 R3 的可靠性为 A3。

那么这个并联系统的可靠性 R = 1 - （1 - R1）x （1 - R2）x （1 - R3）x … x （1 - Rn）。

---

八、总结

本文对软考计算机存储结构进行了复习，包括存储结构概论、局部性原理、Cache 高速缓存、主存地址单元、磁盘存取、计算机总线和串并联的系统可靠性。