#每日一题合集#牛客JZ23-JZ33

为了督促自己每天练一练编程
时间：2022年8月21日-2022年8月31日
网站：https://www.nowcoder.com/exam/oj/ta?tpId=13

8.21-JZ23. 链表中环的入口结点

这个题，找环很容易，快慢指针是否相遇即可；主要是找环的入口结点，这个解释可以参考官方题解：

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};
*/
class Solution {
public:
    ListNode* is_cycle(ListNode* head){
        if(head == NULL)
            return NULL;
        ListNode* slow = head;
        ListNode* fast = head;
        
        while(fast != NULL && fast->next != NULL){
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow)
                return slow;
        }
        return NULL;
    }
    
    ListNode* EntryNodeOfLoop(ListNode* pHead) {
        ListNode* slow = is_cycle(pHead);
        if(slow == NULL)
            return NULL;
        ListNode* fast = pHead;
        while(fast != slow){
            fast = fast->next;
            slow = slow->next;
        }
        return slow;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

8.22-JZ24. 反转链表

很简单的链表内部反转，用个tmp指针记录一下下一个即可

class Solution {
public:
    ListNode* ReverseList(ListNode* pHead) {
        ListNode* cur = pHead;
        ListNode* pre = NULL;
        ListNode* tmp = pHead;
        while(cur != NULL){
            tmp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

8.23-JZ25. 合并两个排序的链表

/*
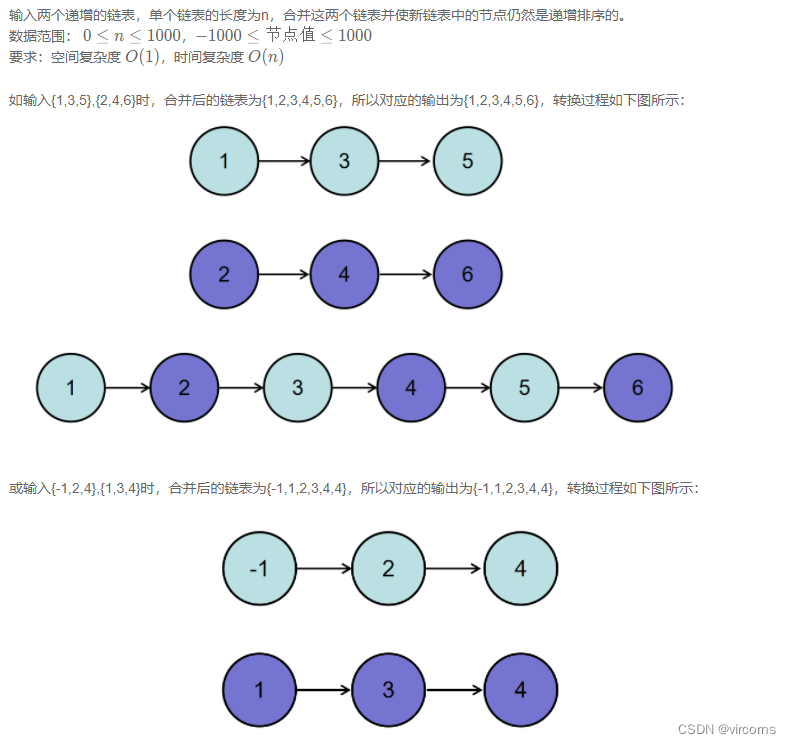
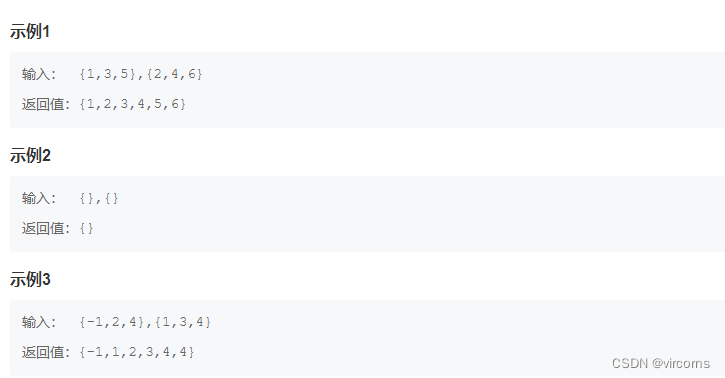
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
        if(pHead1 == NULL)
            return pHead2;
        if(pHead2 == NULL)
            return pHead1;
        ListNode* res = new ListNode(0);
        ListNode* cur = res;
        
        while(pHead1 != NULL && pHead2 != NULL){
            if(pHead1->val < pHead2->val){
                cur->next = pHead1;
                pHead1 = pHead1->next;
            }
            else{
                cur->next = pHead2;
                pHead2 = pHead2->next;
            }
            cur = cur->next;
        }
        if(pHead1 != NULL)
            cur->next = pHead1;
        if(pHead2 != NULL)
            cur->next = pHead2;
        return res->next;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

8.24-JZ26. 树的子结构

        因为空树不是任何树的子树，所以要先判断B树是否为空树。
        当A树为空，但是B树还有节点的时候，不为子树；但是B树到空节点时可以是子树。
        双重遍历：A遍历自己所有的节点当做子树的起点，每次再递归比较是否与B树完全一致

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    bool Judge(TreeNode* root1, TreeNode* root2) {
        if(root1 == NULL && root2 != NULL)
            return false;
        if(root1 == NULL || root2 == NULL)
            return true;
        if(root1->val != root2->val)
            return false;
        return Judge(root1->left, root2->left) && Judge(root1->right, root2->right);
    }
    
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2) {
        if(pRoot2 == NULL)
           return false;
        if(pRoot1 == NULL && pRoot2 != NULL)
            return false;
        if(pRoot1 == NULL || pRoot2 == NULL)
            return true;
        bool flag1 = Judge(pRoot1, pRoot2);
        bool flag2 = HasSubtree(pRoot1->left, pRoot2);
        bool flag3 = HasSubtree(pRoot1->right, pRoot2);  
        return flag1 || flag2 || flag3;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

8.25-JZ27. 二叉树的镜像

非常简单的递归交换

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pRoot TreeNode类 
     * @return TreeNode类
     */
    TreeNode* Mirror(TreeNode* pRoot) {
        // write code here
        if(pRoot == NULL)
            return NULL;
        TreeNode* left = Mirror(pRoot->left);
        TreeNode* right = Mirror(pRoot->right);
        
        pRoot->left = right;
        pRoot->right = left;
        
        return pRoot;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

8.26-JZ28.对称的二叉树

和上一个题思路很像，也是递归判断左右是否一样。

class Solution {
public:
    bool Judge(TreeNode* r1, TreeNode* r2){
        if(r1 == NULL && r2 == NULL)
            return true;
        if(r1 == NULL || r2 == NULL || r1->val != r2->val)
            return false;
        return Judge(r1->left, r2->right) && Judge(r1->right, r2->left);
    }
    
    bool isSymmetrical(TreeNode* pRoot) {
        return Judge(pRoot, pRoot);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

8.27-JZ29. 顺时针打印矩阵

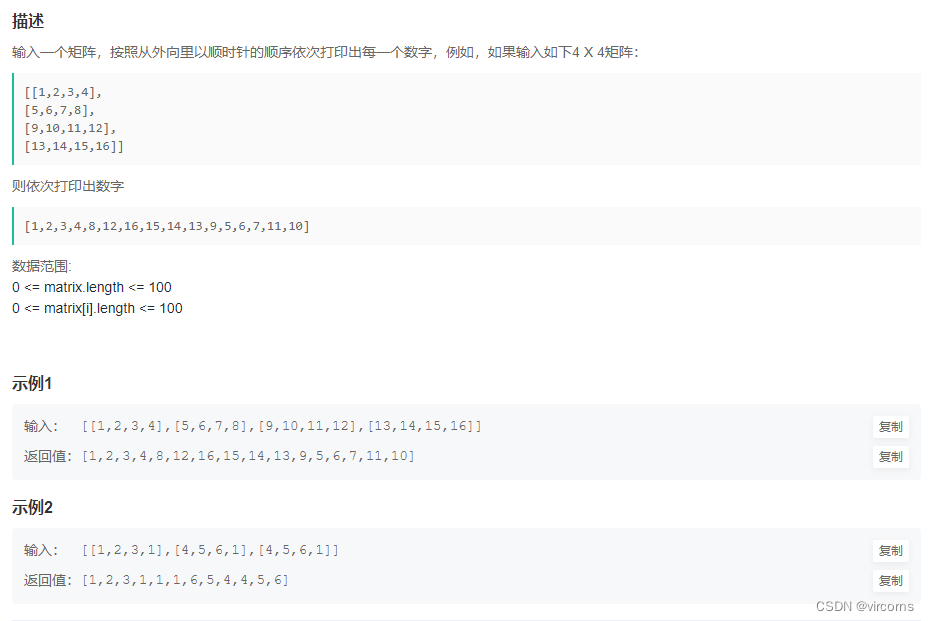
这是一个纯思维题，只要能想到用上下左右来标记判断，上下或左右重合为结束标志。分别对上行、右列、下行、左列进行遍历即可。

class Solution {
public:
    vector<int> printMatrix(vector<vector<int> > matrix) {
        vector<int> res;
        int n = matrix.size();
        if(n == 0)
            return res;
        int left = 0, right = matrix[0].size() - 1;
        int up = 0, down = n - 1;
        int i;
        
        while(left <= right && up <= down){
            for(i = left; i <= right; i++)
                res.push_back(matrix[up][i]);
            up++;
            if(up > down)
                break;
            
            for(i = up; i <= down; i++)
                res.push_back(matrix[i][right]);
            right--;
            if(left > right)
                break;
            
            for(i = right; i >= left; i--)
                res.push_back(matrix[down][i]);
            down--;
            if(up > down)
                break;
            
            for(i = down; i >= up; i--)
                res.push_back(matrix[i][left]);
            left++;
            if(left > right)
                break;
        }
        return res;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

8.28-JZ30. 包含min函数的栈

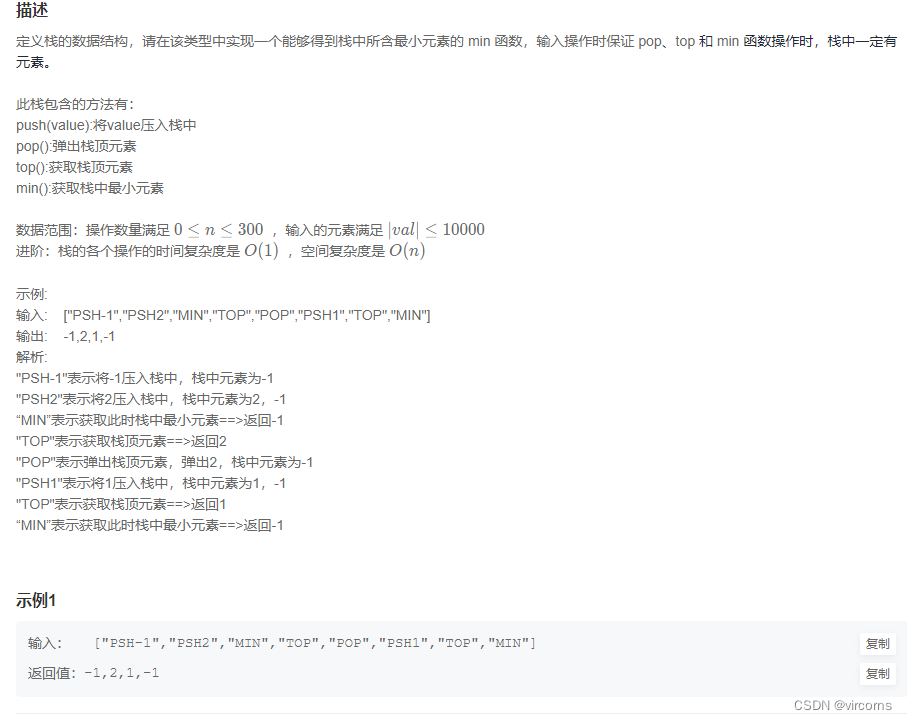
也是比较简单的栈操作，就是用一个栈，每次判断，最小值就存，不是最小值就重复，这样每次栈顶都是现在这个栈的最小值。

class Solution {
public:
    stack<int> s;
    stack<int> m;
    void push(int value) {
        s.push(value);
        if(m.empty() || m.top() > value)
            m.push(value);
        else 
            m.push(m.top());
    }
    void pop() {
        s.pop();
        m.pop();
    }
    int top() {
        return s.top();
    }
    int min() {
        return m.top();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

8.29-JZ31. 栈的压入、弹出序列

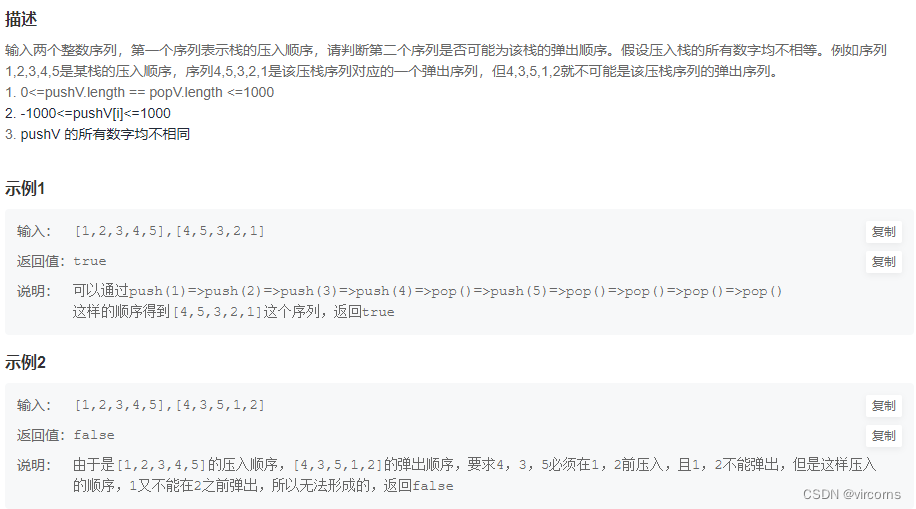
class Solution {
public:
    bool IsPopOrder(vector<int> pushV,vector<int> popV) {
        stack<int> s;
        int n = pushV.size();
        int i = 0;
        for(int j = 0; j < n; j++){
            while(i < n && (s.empty() || s.top() != popV[j])){
                s.push(pushV[i]);
                i++;
            }
            if(s.top() == popV[j])
                s.pop();
            else
                return false;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

8.30-JZ32.从上往下打印二叉树

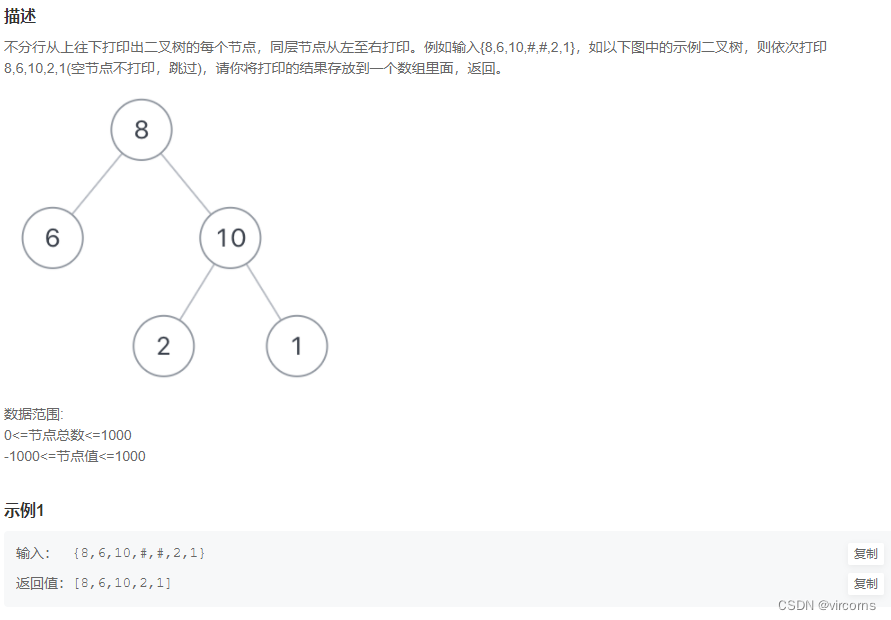
二叉树的层次遍历基础写法了。利用队列遍历节点，如果有左右子节点，就依次放队伍后面；

class Solution {
public:
    vector<int> PrintFromTopToBottom(TreeNode* root) {
        vector<int> res;
        if(root == NULL)
            return res;
        queue<TreeNode*> q;
        q.push(root);
        TreeNode* cur;
        
        while(!q.empty()){
            cur = q.front();
            q.pop();
            res.push_back(cur->val);
            
            if(cur->left)
                q.push(cur->left);
            if(cur->right)
                q.push(cur->right);
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

8.31-JZ33. 二叉搜索树的后序遍历序列

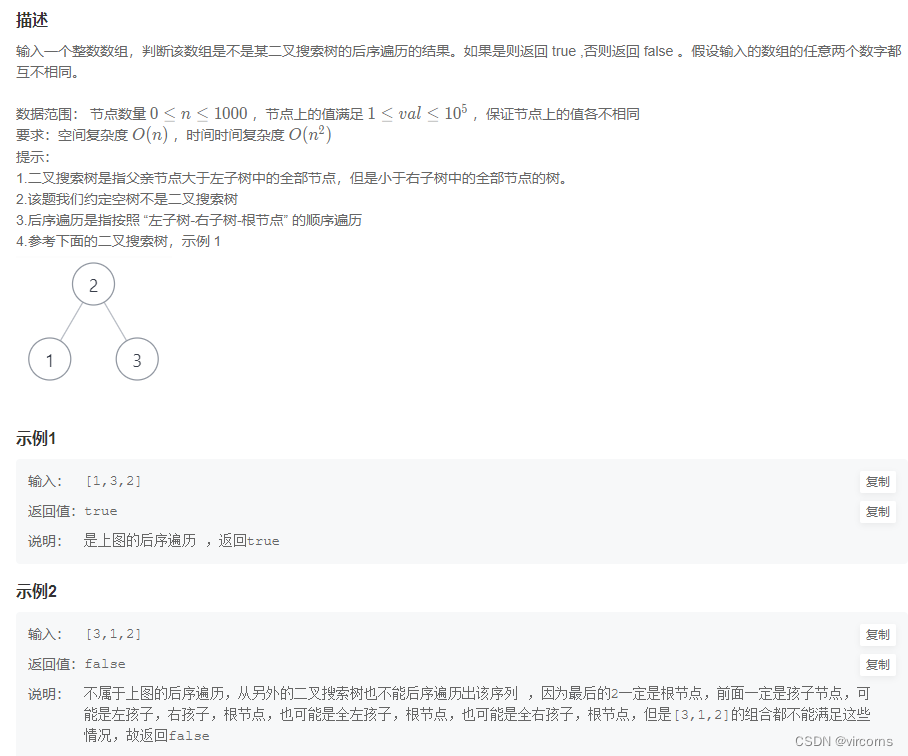
递归最重要的是找到左右子树的分界点，如果他是一个二叉搜索树，那么他的左边一定都比根节点小，那么从0到最后一个比根节点小的都是左子树；同理，从第一个比根节点大的位置到根节点前一个，都是右子树。如果能一直这样划分，说明是二叉搜索树，否则不是。
注意：递归的边界一定要写对，否则会超时

class Solution {
public:
    bool Judge(vector<int> sequence,int begin, int end){
        int flag = 1;
        if(begin > end)
           return true;
        int left = -1, right = end, root = sequence[end];
        for(int i = begin; i <= end; i++){
            if(sequence[i] < root){
                left = i;
            }
            if(flag && sequence[i] > root){
                right = i;
                flag = 0;
            }
        }
//         for(int i = begin; i <= end; i++){
//             if(sequence[i] > root){
//                 right = i;
//                 break;
//             }
//         }
        if(left > right)
            return false;
        
        return Judge(sequence, begin, left) && Judge(sequence, right, end-1);
    }
    bool VerifySquenceOfBST(vector<int> sequence) {
        int n = sequence.size();
        if(n == 0)
            return false;
        return Judge(sequence, 0, n-1);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34