贪心算法题

贪心算法

1. 455. 分发饼干

问题

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。
1
2
3
4
5
6

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
1
2
3
4
5
6

提示：

• 1 <= g.length <= 3 * 104
• 0 <= s.length <= 3 * 104
• 1 <= g[i], s[j] <= 231 - 1

代码

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int index = 0;
        int result = 0;
        for(int i = 0; i < g.length && index < s.length; i++){
            if(g[i] <= s[index]) {
                // 吃掉
                result++;
            } else {
                i--;
            }
            index++;
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

2. 376. 摆动序列

问题

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。
1
2
3

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
1
2
3
4

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2
1
2

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000

代码

• 贪心法

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int curDiff = 0;
        int preDiff = 0;
        int result = 1; // 考虑 右 边界值 特殊情况
        for(int i = 0; i < nums.length - 1; i++) {
            // 考虑了 左边界值 特殊情况
            curDiff = nums[i] - nums[i + 1];
            if(curDiff < 0 && preDiff >= 0 || curDiff > 0 && preDiff <= 0) {
                result++;
                preDiff = curDiff;
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

• 动态规划

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int n = nums.length;
        if(n < 2) return n;
        int up = 1;
        int down = 1;
        for(int i = 1; i < n; i++) {
            if(nums[i] < nums[i - 1]) {
                down = up + 1;
            }
            if(nums[i] > nums[i - 1]) {
                up = down + 1;
            }
        }
        return Math.max(up, down);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

3. 53. 最大子数组和

问题

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

1
2
3
4

示例 2：

输入：nums = [1]
输出：1
1
2

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23
1
2

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104

代码

class Solution {
    public int maxSubArray(int[] nums) {
        int res = - 10000;
        int sum = 0;
        for(int i = 0; i < nums.length; i++) {
            sum += nums[i];
            if(sum > res) {
                res = sum;
            }
            if(sum < 0) {
                sum = 0;
            }      
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

4. 122. 买卖股票的最佳时机 II

问题

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
     总利润为 4 + 3 = 7 。
1
2
3
4
5

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     总利润为 4 。
1
2
3
4

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。
1
2
3

提示：

• 1 <= prices.length <= 3 * 104
• 0 <= prices[i] <= 104

代码

• 直接写法

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length < 2) {
            return 0;
        }
        int res = 0;
        for(int i = 0; i < prices.length - 1; i++) {
            int pricesDiff = prices[i + 1] - prices[i];
            if(pricesDiff > 0) {
                res += pricesDiff;
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• 贪心写法

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length < 2) {
            return 0;
        }
        int res = 0;
        for(int i = 0; i < prices.length - 1; i++) {
            res += Math.max(prices[i + 1] - prices[i], 0);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

• 动态规划

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        if(n < 2) {
            return 0;
        }
        int[][] dp = new int[n][2];
        // 表示 买进第 0 天的股
        dp[0][0] -= prices[0];
        //默认初始：dp[0][1] = 0; 表示初始收益为 0 
        for(int i = 1; i < n; i++) {
            // 股票下跌，买进
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            // 股票上涨，卖出
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return Math.max(dp[n - 1][0], dp[n - 1][1]);
    }
} 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

5. 55. 跳跃游戏

问题

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
1
2
3

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。
1
2
3

提示：

• 1 <= nums.length <= 3 * 104
• 0 <= nums[i] <= 105

代码

class Solution {
    public boolean canJump(int[] nums) {
        if(nums.length == 1) return true;
        // 可到达的 最长下标
        int cover = 0;
        for(int i = 0; i <= cover; i++) {
            cover = Math.max(cover, i + nums[i]);
            if(cover >= nums.length - 1) return true;
        }
        return false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

6. 45. 跳跃游戏 II

问题

给你一个非负整数数组 nums ，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

假设你总是可以到达数组的最后一个位置。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。
1
2
3
4

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2
1
2

提示:

• 1 <= nums.length <= 104
• 0 <= nums[i] <= 1000

代码

• 版本一

class Solution {
    public int jump(int[] nums) {
        if(nums.length == 1) {
            return 0;
        }
        int curDistance = nums[0];
        int nextDistance = 0;
        int ans = 0;;
        int n = nums.length;
        for(int i = 0; i < n; i++) {
            nextDistance = Math.max(nextDistance, nums[i] + i);
            // 如果当前 最远步长 已经达到终点下标了，
            if(curDistance >= n - 1) {
                ans++;
                break;
            }
            //否则 看是否已经 满足 当前下标是 最远步长
            // 主要是为了更新 nextDistance 为 在当前下标到 最远步长中 找到 下一个最远步长下标最远的
            if(i == curDistance) {
                ans++;          
                curDistance = nextDistance;            
            }
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

• 版本二

class Solution {
    public int jump(int[] nums) {
        if(nums.length == 1) {
            return 0;
        }
        int curDistance = 0;
        int nextDistance = 0;
        int ans = 0;;
        int n = nums.length;
        for(int i = 0; i < n - 1; i++) {
            nextDistance = Math.max(nextDistance, nums[i] + i);
            //否则 看是否已经 满足 当前下标是 最远步长
            // 主要是为了更新 nextDistance 为 在当前下标到 最远步长中 找到 下一个最远步长下标最远的
            if(i == curDistance) {
                ans++;          
                curDistance = nextDistance;            
            }
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

7. 1005. K 次取反后最大化的数组和

问题

给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

以这种方式修改数组后，返回数组 可能的最大和 。

示例 1：

输入：nums = [4,2,3], k = 1
输出：5
解释：选择下标 1 ，nums 变为 [4,-2,3] 。

1
2
3
4

示例 2：

输入：nums = [3,-1,0,2], k = 3
输出：6
解释：选择下标 (1, 2, 2) ，nums 变为 [3,1,0,2] 。
1
2
3

示例 3：

输入：nums = [2,-3,-1,5,-4], k = 2
输出：13
解释：选择下标 (1, 4) ，nums 变为 [2,3,-1,5,4] 。
1
2
3

提示：

• 1 <= nums.length <= 104
• -100 <= nums[i] <= 100
• 1 <= k <= 104

代码

• 绝对值排序

class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        nums = IntStream.of(nums).boxed().sorted((t1, t2) -> Math.abs(t2) - Math.abs(t1)).mapToInt(Integer::intValue).toArray();
        for(int i = 0; i < nums.length; i++) {
            if(nums[i] < 0 && k > 0) {
                nums[i] = - nums[i];
                k--;
            }
        }
        if(k % 2 == 1) {
            nums[nums.length - 1] = - nums[nums.length - 1];
        }
        return Arrays.stream(nums).sum();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• 从小到大排序

class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        int n = nums.length;
        if(n == 1) return k % 2 == 0 ? nums[0] : -nums[0];
        int sum = 0;
        int index = 0;
        Arrays.sort(nums);
        for(int i = 0; i < k; i++) {
            if(i < nums.length - 1 && nums[i] < 0) {
                nums[i] = -nums[i];
                if(nums[i] >= Math.abs(nums[i + 1])) index++;
                continue;
            }
            nums[index] = -nums[index];
        }

        for(int i = 0; i < nums.length; i++) {
            sum += nums[i];
        }
        return sum;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

8. 134. 加油站

问题

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

示例 1:

输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。
1
2
3
4
5
6
7
8
9
10

示例 2:

输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。
1
2
3
4
5
6
7
8
9

提示:

• gas.length == n
• cost.length == n
• 1 <= n <= 105
• 0 <= gas[i], cost[i] <= 104

代码

• 暴力法

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int curGas = 0;
        for(int i = 0; i < gas.length; i++) {
            curGas = gas[i] - cost[i];
            int index = (i + 1) % gas.length;
            while(curGas >= 0 && index != i) {
                curGas += gas[index] - cost[index];
                index = (index + 1) % gas.length;
            }
            if(curGas >= 0) {
                return i;
            }
        }
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

• 贪心算法1

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int curSum = 0;
        int min = Integer.MAX_VALUE;
        for(int i = 0; i < gas.length; i++) {
            int res = gas[i] - cost[i];
            curSum += res;
            if(curSum < min) {
                min = curSum;
            }
        }
        if(curSum < 0) return -1;
        if(min >= 0) return 0;
        for(int i = gas.length - 1; i >= 0; i--) {
            int res = gas[i] - cost[i];
            min += res;
            if(min >= 0) return i;
        }
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

• 贪心算法2

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int curSum = 0;
        int totalSum = 0;
        int startIndex = 0;
        for(int i = 0; i < gas.length; i++) {
            int res = gas[i] - cost[i];
            curSum += res;
            totalSum += res;
            if(curSum < 0) {
                startIndex = i + 1;
                curSum = 0;
            }     
        }
        if(totalSum < 0) return -1;
        return startIndex;

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

9. 135. 分发糖果

问题

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例 1：

输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
1
2
3

示例 2：

输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。
1
2
3
4

提示：

• n == ratings.length
• 1 <= n <= 2 * 104
• 0 <= ratings[i] <= 2 * 104

代码

class Solution {
    public int candy(int[] ratings) {
        if(ratings.length == 1) {
            return 1;
        }
        int n = ratings.length;
        int[] candyArg = new int[n];
        for(int i = 0; i < n; i++) {
            candyArg[i] = 1;
        }
        for(int i = 0; i < n - 1; i++) {
            if(ratings[i + 1] > ratings[i]) candyArg[i + 1] = candyArg[i] + 1;
        }
        for(int i = n - 2; i >= 0; i--) {
            if(ratings[i] > ratings[i + 1]) candyArg[i] = Math.max(candyArg[i], candyArg[i + 1] + 1);
        }
        int sum = 0;
        for(int i = 0;  i < n; i++) {
            sum += candyArg[i];
        }
        return sum;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

10. 860. 柠檬水找零

问题

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例1：

输入：bills = [5,5,5,10,20]
输出：true
解释：
前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零，所以我们输出 true。
1
2
3
4
5
6
7

示例2：

输入：bills = [5,5,10,10,20]
输出：false
解释：
前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。
对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零，所以答案是 false。
1
2
3
4
5
6
7

提示：

• 1 <= bills.length <= 105
• bills[i] 不是 5 就是 10 或是 20

代码

class Solution {
    public boolean lemonadeChange(int[] bills) {
        int five = 0, ten = 0, twenty = 0;
        for(int i = 0; i < bills.length; i++) {
            if(bills[i] == 5) {
                five++;
            }
            if(bills[i] == 10) {
                if(five <= 0) return false;
                ten++;
                five--;
            }
            if(bills[i] == 20) {
                if(five > 0 && ten > 0) {
                    five--;
                    ten--;
                    twenty++;
                } else if(five >= 3) {
                    five -= 3;
                    twenty++;
                } else {
                    return false;
                }
            }
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

11. 406. 根据身高重建队列

问题

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

示例 1：

输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
1
2
3
4
5
6
7
8
9
10

示例 2：

输入：people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出：[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
1
2

提示：

• 1 <= people.length <= 2000
• 0 <= hi <= 106
• 0 <= ki < people.length
• 题目数据确保队列可以被重建

代码

class Solution {
    public int[][] reconstructQueue(int[][] people) {
        int length = people.length;
        Arrays.sort(people, new Comparator<int[]>(){
            public int compare(int[] people1, int[] people2) {
                // 从大到小 排序
                if(people2[0] == people1[0]) {
                    return people1[1] - people2[1];
                }else {
                    return people2[0] - people1[0];
                }
            }
        });
        for(int i = 0; i < length; i++) {
            inset(people, i, people[i][1]);
        }
        return people;
    }

    private void inset(int[][] people, int sourceIndex,  int destIndex) {
        int[] temp = people[sourceIndex];
        if(sourceIndex <= destIndex) {
            for(int i = sourceIndex; i < destIndex; i++) {
                people[i] = people[i + 1];
            }
            people[destIndex] = temp;
        } else {
            for(int i = sourceIndex; i > destIndex; i--) {
                people[i] = people[i - 1];
            }
            people[destIndex] = temp;
        }
    }
}	
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

12. 452. 用最少数量的箭引爆气球

问题

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。
1
2
3
4
5

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。
1
2
3

示例 3：

输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：气球可以用2支箭来爆破:
- 在x = 2处发射箭，击破气球[1,2]和[2,3]。
- 在x = 4处射出箭，击破气球[3,4]和[4,5]。
1
2
3
4
5

提示:

• 1 <= points.length <= 105
• points[i].length == 2
• -231 <= xstart < xend <= 231 - 1

代码

class Solution {
    public int findMinArrowShots(int[][] points) {
        Arrays.sort(points, (a,b) -> {
            if(a[0] != b[0]) {
                return (long)a[0] - (long)b[0] > 0 ? 1 : -1;
            }
            return  (long)a[0] - (long)b[0] > 0 ? 1 : -1;
        });
        int count = 0;
        for(int i = 1; i < points.length; i++) {
            if(points[i][0] > points[i - 1][1]) {
                count++;
            } else {
                points[i][1] = Math.min(points[i][1], points[i - 1][1]);
            }
        }
        return count + 1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

先排序（按元素0号下标升序）后贪左边，因为排完后，前面的肯定包含后面的元素，再去贪右边边界，贪最小边界。

13. 435. 无重叠区间

问题

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

示例 1:

输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。
1
2
3

示例 2:

输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
1
2
3

示例 3:

输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。
1
2
3

提示:

• 1 <= intervals.length <= 105
• intervals[i].length == 2
• -5 * 104 <= starti < endi <= 5 * 104

代码

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        // 对右区间升序，
        Arrays.sort(intervals, (a,b) -> {
            return a[1] - b[1];
        });
        int removeCount = 0;
        for(int i = 1; i < intervals.length; i++) {
            if(intervals[i][0] < intervals[i - 1][1]) {
                removeCount++;
                // 更新当前状态下不重叠右区间上限
                // 不用理会两个区间中间可能留下的空白区域，因为已经排序
                // 所以后面的区间不会重叠中间那块空白区域
                intervals[i][1] = intervals[i - 1][1];
            }
        }
        return removeCount;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

14. 714. 买卖股票的最佳时机含手续费

问题

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1：

输入：prices = [1, 3, 2, 8, 4, 9], fee = 2
输出：8
解释：能够达到的最大利润:  
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8
1
2
3
4
5
6
7
8

示例 2：

输入：prices = [1,3,7,5,10,3], fee = 3
输出：6
1
2

提示：

• 1 <= prices.length <= 5 * 104
• 1 <= prices[i] < 5 * 104
• 0 <= fee < 5 * 104

代码

class Solution {
    public int maxProfit(int[] prices, int fee) {
        // 买入是先 算手续费，buy 是买入+手续费
        int buy = prices[0] + fee;
        int result = 0;
        for(int i = 1; i < prices.length; i++) {
            // buy 已经更新为能否继续收益的更高水准
            // 如果不能继续收益了，也就是跌股了，那就卖掉上一股，重新买入新股
            // 因为相比 同一股 会有更大的收益
            if(prices[i] + fee < buy) {
                buy = prices[i] + fee;
            }
            if(prices[i] > buy) {
                result += prices[i] - buy;
                // 连续涨股就持股
                buy = prices[i];
            }
        }
        return result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

15. 968. 监控二叉树

问题

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

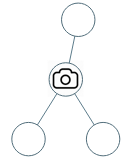
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。
1
2
3

示例 2：

输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
1
2
3

提示：

• 给定树的节点数的范围是 [1, 1000]。
• 每个节点的值都是 0。

代码

class Solution {
    int res = 0;
    public int minCameraCover(TreeNode root) {
        if(traversal(root) == 0) return ++res;
        return res;
    }
    // 0 - 无覆盖 1 - 有摄像头 2 - 有覆盖
    private int traversal(TreeNode node) {
        // 终止条件
        if(node == null) return 2;

        // 后序递归遍历
        int left = traversal(node.left);
        int right = traversal(node.right);
        // 设置叶子节点为 未覆盖，或者是 两个子节点均已覆盖。那么设置该节点为未覆盖
        if(left == 2 && right == 2) {
            return 0;
        }
        // 存在子节点还未覆盖，该节点设置摄像头
        if(left == 0 || right == 0) {
            res++;
            return 1;
        }
        // 子节点有摄像头，该节点设置为覆盖
        if(left == 1 || right == 1) {
            return 2;
        }
        // 因为逻辑返回需要，虽然不会到这一步但还是要写
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

结束语

评论区可留言，可私信，可互相交流学习，共同进步，欢迎各位给出意见或评价，本人致力于做到优质文章，希望能有幸拜读各位的建议！

专注品质，热爱生活。
交流技术，寻求同志。

—— 嗝屁小孩纸 QQ：1160886967

—— 其他平台：CSDN、51CTO、博客园

—— 转发于个人博客对应 贪心算法 题型

—— GitHub 专栏：Fyupeng