-
自己动手写编译器:词法解析的系统化研究
在前面章节中,我们千辛万苦的做了一个可以将部分c语言代码进行解析并编译成中间语言的微型编译器,通过实践我们对编译技术的整体架构和实现原理有了一定的感性认识,实现了“没吃过猪肉但见过猪跑”,从本节开始,我们正式进入“吃猪肉”的过程,我们将非常系统的去研究编译原理各部分理论和算法,从这节开始,我们系统化的去剖析词法解析的算法流程。
前面我们实现过词法解析,他的大概流程是,将文本读入,然后从文本中取出一个单位字符串,分析它的成分,到底是变量,数字,还是关键字,然后给他创建一个抽象描述对象叫token,于是源码字符串文本就变成了token的集合,而语法分析的主要任务是通过分析token集合所描述的含义来建立抽象语法树,并最终将代码转义成机器码或是中间代码。
但是我们以前实现的词法解析比较“低层次”,也就是我们写死了词法解析的规则。也就是我们的词法解析只能识别特定语言的字符串,例如我们原来实现的词法解析只能识别部分c语言代码。事实上词法解析还有更高层次,那就是它识别的不是具体的语言,而是给定的“规则”,这种词法解析能力也叫词法解析生成器。如今编译器开发早已经形成了一个完善的工具链,词法解析器不仅能用于解析c语言代码,也能用来解析python, java等,只要你给他既定的词法规则,他就能生成我们前面实现的,能执行针对特定语言的词法解析代码,因此它也成为词法解析引擎。
下面我们需要了解三个比较抽象的概念:
token: 他是程序意义上的一个抽象对象,他包含一个数值,用来描述一个字符串单元所属类别,同时还包含他所针对的字符串,同时还包含一些其他信息,例如它所描述字符串所在的行号,文件等,这个概念我们在前面实践中早有体会。pattern: 他用来描述特定token类别所要求的字符组合规律,例如ID,他对应的pattern就是“由字符和数字组成,同时字符作为开头的字符集合",pattern是词法解析的核心,后面我们会看到有很多复杂且精妙的算法和数据结构来实现pattern对应的识别能力。显然所有能满足一个给定组合规律的字符串都属于一个token类别
lexeme,这个概念我们前面也了解过,他就是一系列字符组成的字符串,而且这些字符的组合满足pattern描述的要求。我们看一个具体例子:
print("Total = ", score)- 1
在这条语句中 print, score 属于lexeme,他们对应的token是ID, 同时Total= 对应的token是literal,也就是字符串。当特定字符组成的字符串满足特定pattern,或者说是组合规律时,词法解析器就会创建一个对应的token对象来对这些字符串集合进行抽象意义上的描述。但是token不仅仅要描述抽象上的性质,还要包含具体的属性,例如数字0,1都属于类别NUM,但是对编译器而言,知道类别NUM对应的数值至关重要,因此token除了描述类别外,还需要描述类别的具体对象,如果了解面向对象的编程,那么token就包含了类的定义和类的具体实例。
在进行词法解析时,我们还需要执行一定的缓存。前面实践我们也看到,在识别字符串属于那种类别时,我们通常需要读取下一个字符来决定,例如当前读到的符号是"=“那么我们需要看下一个符号,如果下一个符号是”=",那意味着两个‘=’符号必须合并在一起解读。通常我们会把一个磁盘区块的内容读入内存,通常是4096个字节,然后用两个指针来读取字符,第一个指针叫lexmeBegin,指向当前字符串的开头,另一个指针forward从lexemeBegin位置开始不断后移,直到两个指针中间字符组合满足给定匹配规则,也就是patter为止,然后下一次读取时lexemeBegin指向当前forward所在位置的下一个字符:
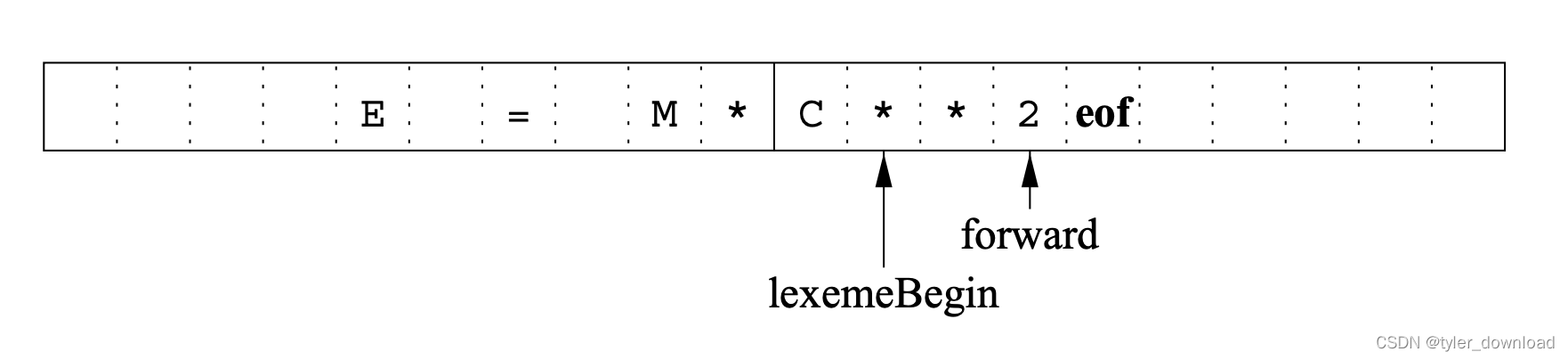
其中eof是一个特定符号,它表示文本结束,后面不再存有有效字符。这点我们在前面实现中也体会过。下面我们要探寻一些较为抽象的概念,例如”字符“,”字符串“ 和 ”语言“。首先”语言“是对满足特定条件元素集合的描述,例如所有满足c语言语法规则的字符串文本都叫c“语言”,显然这个集合的元素个数为无限,因为我们可以用c语言写出不同样的程序。对于二进制数而言,它的字符只有两个,分别为0和1,那么由0和1排列组合而成的所有字符串所形成的集合也是一种“语言”。而一个特定的字符集合就叫”字符串“。
这里有一个递进的层次关系,最底层的就是”字符“,例如英语中的26个字母。接着是字符串,也就是字符按照某种规则组成的集合,例如"hello",在英语中就是单词。最后就是语言,也就是字符串按照某种指定规则形成的集合,例如英语。我们这里谈到“某种规则”,我们需要使用一些特定的数学符号来对其进行描述,对人类语言而言,目前我们找不到数学或逻辑的方式来描述其组成规则,但对编程语言而言,我们不难找到。
首先我们规定字符集合的几种运算,假设我们有两个字符集合L={a,b…,z, A,B…Z}, D={0,1,2…9},针对这两个字符集合,我们定义如下运算或操作:
1, L ∪ D 表示在两个集合的并,于是结果就是{a, … z, A…Z, 0… 9},
2,LD,表示在L中选择一个字符,然后D中选择一个字符,两者前后连接,由于L中有52个字符,D中有10个字符,因此这种连接结果总共有520种,于是LD集合包含520个元素
3, L 4 L^4 L4 表示从L中任意选择4个字符形成字符串,因此该集合的元素个数就是 2 6 4 26^4 264
4, L ∗ L^* L∗ 表示从L中选取0个或任意多个字符进行组合,如果是0个的话,对应的结果就是空集。
5, L + L^+ L+表示从L中选择1个或任意多个字符进行组合,因此它是情况4中排除掉空集的结果有了上面描述的运算后,我们就能描述字符的特定组合规则,而这种描述方式是所谓的“正则表达式”。 我们利用上面规则就能描述C语言中变量名的组合方式:
letter_ ( l e t t e r ∣ d i g i t ) ∗ (letter_|digit)^* (letter∣digit)∗
它表示以字符或下划线开始,后面跟着任意多个字符,下划线或数字的组合。其中“|”表示“或”,下面我们需要看看有点烧脑的逻辑描述,我们看到给定正则表达式,例如上面那个,那么他就定义了一种字符串集合,所有满足正则表达式规定的字符串的集合就叫做对应正则表达式的语言,如果我们用r来表示给定正则表达式,用L®表示所有满足r的字符串的集合,也就是L®表示表达式r生成的语言,其实我们也可以把L®看成一种函数映射,给定一个表达式后,它“映射”出一个字符串集合,这里我们给这个“映射”增加几个越苏条件:
1, ϵ \epsilon ϵ表示一个空表达式,那么L( ϵ \epsilon ϵ)映射出一个空的字符串集合
2,我们用 ∑ \sum ∑ 表示一个字符集合,例如26个字母的集合就是 ∑ \sum ∑={a,b…z},如果a是集合中的一个字符,那么它本身也自然是一个表达式,同时有L(a) = {a},也就是对于映射L,如果输入是单个字符,那么他生成的集合仅仅包含这个字符。
3,如果r 和 s 分别是两个正则表达式,®|(s)是两个表达式的“并”组合,那么由®|(s)表达式生成的语言对应r和s各自生成语言的并, 也就是L(®|(s)) = L ( r ) ∪ L ( s ) L(r) \cup L(s) L(r)∪L(s)
4, r 和 s是两个正则表达式,表达式®(s)对应的字符串集合或语言就是 L(®(s)) = L®L(s),L®L(s)它表示字符串的前缀部分来着L®,后缀部分来自L(s)。5, r是一个表达式, r ∗ r^* r∗也是一个表达式,他对应的语言或字符串集合就是 L ( r ) ∗ L(r)^* L(r)∗
6,r 是一个表达式, ( r )同样也是一个表达式,同时L( (r ) ) = L( r ) ,也就是我们给一个表达式加上括号后所得的新表达式,他所形成的语言给原来一样。
7,如同四折运算,括号的作用表示优先级,同时在运算中乘法和除法的优先级高于加法和减法,在正则表达式中不同操作符也一样有优先级,其中*操作的优先级最高,而且他总是作用于左边的表达式,例如r*s 等价于(r*)s
8,连接操作符具有第二优先级,| 具有最低优先级,也就是rs|z,表示(rs)|z上面这组规则比较抽象不好理解,应该是一个“劝退点”,不过后面我们通过代码实现就能比较容易的理解这些抽象规则。我们看一个例子:
假设字符集包含两个字符 ∑ \sum ∑={a,b}, 那么表达式 a | b = {a, b}, (a|b)(a|b)={aa, ab, ba, bb}, a ∗ a^* a∗ = { ϵ \epsilon ϵ, a, aa, aaa, …}。(a|b)* 表示所有包含0个或多个a或b组成的字符串,也就是{ ϵ \epsilon ϵ, a, b, ab, aab, aaab, ba, bba, bbba, …},a|a*b表示集合{a, b, ab, aab, aaab…}。如果给定两个正则表达式,r, s,倘若他们各自生成的字符串集合完全相同,那么我们就定义 r = s,例如(a|b) = (b|a),正则表达式在运算符 | , * 下有特定的代数性质:
1,交换律: r | s = s | r ,
2,结合律:r | (s | t) = (r | s) | t
3,分配律:r ( s | t) = rs | rt ,(r|s) | t = rt | st
4, ϵ \epsilon ϵr = r ϵ \epsilon ϵ = r , 这里 ϵ \epsilon ϵ,类似于乘法中的数字1
5, r ∗ r^* r∗ = ( r ∣ ϵ ) ∗ (r | \epsilon)^* (r∣ϵ)∗
6, r ∗ r^* r∗ ∗ ^* ∗ = r ∗ r^* r∗为了简化对正则表达式的描述,我们可以给表达式“起名字”,后面我们在描述中就可以使用名字来指代给定表达式,这种方法也叫正则定义,我们用 ∑ \sum ∑表示字符集,那么正则定义具有如下形式:
d 1 d_{1} d1 -> r 1 r_{1} r1
d 2 d_{2} d2 -> r 2 r_{2} r2
…
d n d_{n} dn -> r n r_{n} rn其中 d i d_{i} di 是不在集合 ∑ \sum ∑中的符号,同时 d i d_{i} di != d j d_{j} dj 如果i != j。并且 r 1 r_{1} r1是基于字符集合 ∑ \sum ∑上的正则表达式。通过这种定义方式,我们可以有效简化嵌套表达式的描述,例子如下:
letter_ -> A | B … | Z | a | b …|z _
digit -> 0 | 1 | 2 | …| 9
id -> letter_ (letter_ | digit) *对于整数,浮点数如:5280, 0.01234, 6.336E4, 1.89E-4,等,他们对应的表达式定义如下:
digit -> 0 | 1 … | 9
digits -> digit digit*
optionalFraction -> . digits | ϵ \epsilon ϵ
optionalExponent -> (E (+ | - | ϵ \epsilon ϵ) digits) | ϵ \epsilon ϵ
number -> digits optionalFraction optionalExponent正则表达式的操作符除了上面描述的*, |,之外,还有一些扩展,分别是 r + r^+ r+表示r至少要重复一次,同时有L( r + r^+ r+) = ( L ( r ) ) + (L( r ))^+ (L(r))+,还有操作符?,他表示给定表达式出现0次或1次,也就是r? = r | ϵ \epsilon ϵ, 同时有L(r?) = L ( r ) ∪ ϵ L(r) \cup \epsilon L(r)∪ϵ,同时操作符*, ?, + 拥有相同的优先级。同时我们还需要知道有一种表达式叫字符集类,也就是r = a 1 , ∣ a 2 , … , a n a_{1}, | a_{2}, \dots, a_{n} a1,∣a2,…,an,其中 a 1 a_{1} a1是属于集合 ∑ \sum ∑中的字符,这种表达式也可以写为[ a 1 a 2 … a n a_{1} a_{2}\dots a_{n} a1a2…an], 同时[a-z]表示[a|b|c|…|z],于是上面的例子我们又可以进一步简化:
letter_ -> [a-zA-z]
digit-> [0-9]
id ->letter_ ( l e t t e r ∣ d i g i t ) ∗ (letter | digit)^* (letter∣digit)∗本节我们描述的理论不好理解,也比较枯燥,因此我们大概了解一下就行,后面我们会通过代码以更加形象和具体的方式来体会这里描述的内容,更多内容请在B站搜索coding迪斯尼。
-
相关阅读:
基于区块链的去中心化数字身份研究及验证
ToPrimitive原理
口袋参谋:如何实时监控对手数据?
10个前端开发常用的速查网站
香港金融科技周VERTU CSO Sophie谈Web3.0的下一个风口 手机虚拟货币移动支付
http与https
代替虚拟化云安全工程师的解决方案
UTONMOS:布局的“元宇宙”未来产生哪些影响?
docker保存镜像出错
Linux 中如何安全地抹去磁盘数据?
- 原文地址:https://blog.csdn.net/tyler_download/article/details/126568638