C++ - 8月31日 - 约瑟夫环问题

目录

目录

问题描述：

举例分析：

代码实现： 

方法一：数组

方法二：递归

代码实现：

方法二：递归：

参考资料：

---

问题描述：

约瑟夫环（约瑟夫问题）是一个数学的应用问题：已知n个人（以编号1，2，3，...n分别表示）围坐在一张圆桌周围，从编号为k的人开始报数，数到m的那个人出圈，他的下一个人又从1开始报数，数到m的那个人又出圈；按照这个规律一直重复下去，最后一个出局的人为游戏的最终胜利者。

举例分析：

例如：我们现在假设有10个人围成一圈进行约瑟夫环游戏，每个人的编号为0-9，现在规定数到3的人出圈，我们在画板上分析此过程：

初始状态为：

我们从编号为0的人开始报数，编号0报数为1， 编号1报数为2，编号2报数为3，现在编号为2的人出局：

现在我们从编号为3的人开始重新报数，编号3报数为1，编号4报数为2，编号5报数为3，编号5出局：

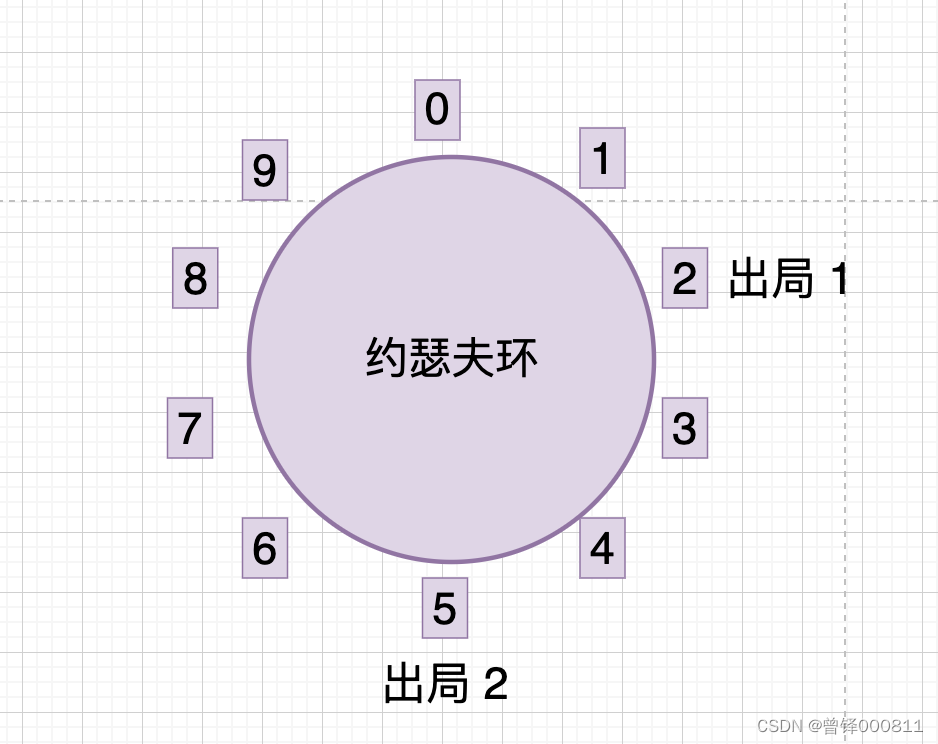
现在从编号为6的人开始报数，编号6的人报数为1 ，编号7的人报数为2，编号8的人报数为3，编号8的人出局：

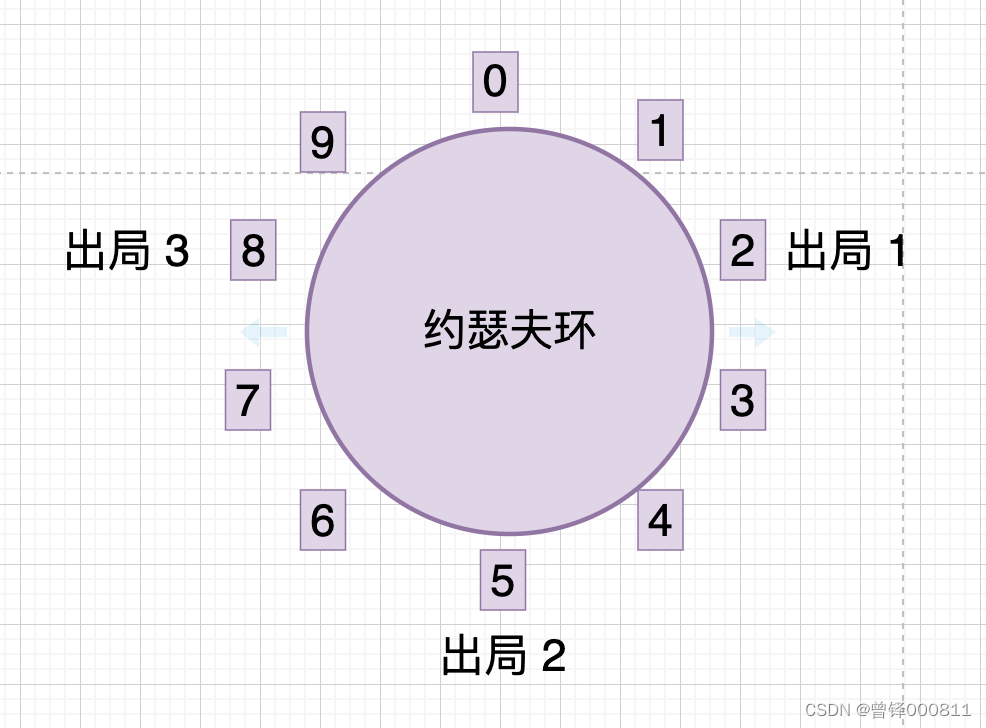
 现在从编号为9的人开始报数，编号9的人报数为1 ，编号0的人报数为2，编号1的人报数为3，编号1的人出局：

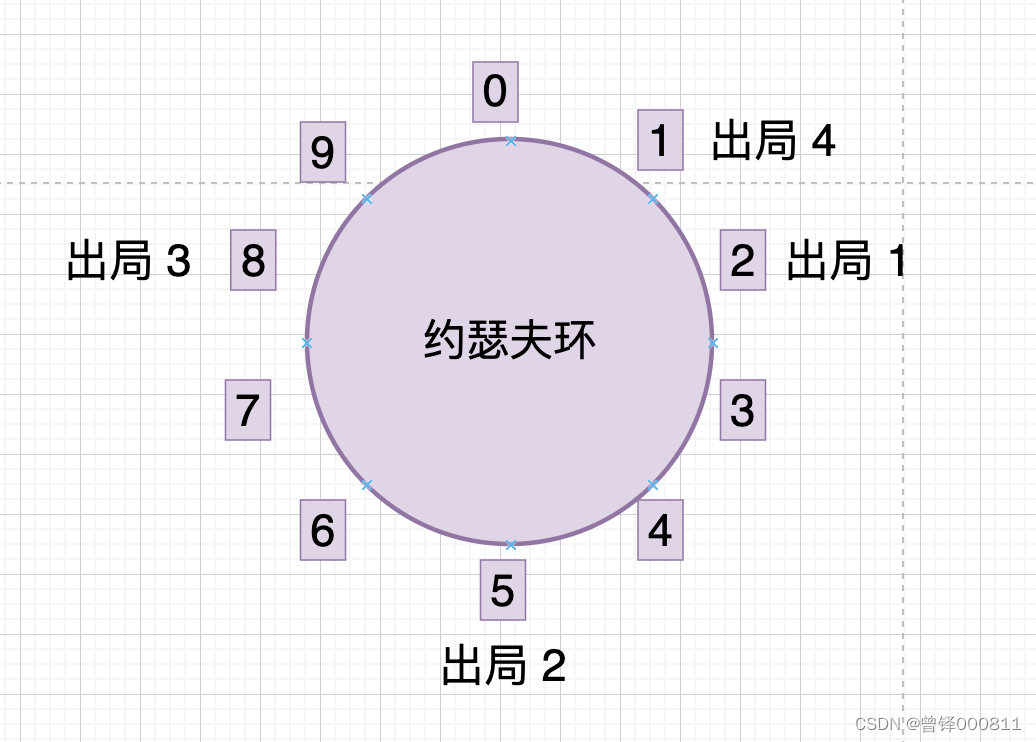
现在本来应该从编号1后面的那个人开始报数，但是编号2的人在第一轮已经出局，所以我们直接跳过编号为2的人，从编号为3的人开始报数，编号3的人报数为1 ，编号4的人报数为2，将第二轮出局的编号5跳过，编号6的人报数为3，编号6的人出局： 

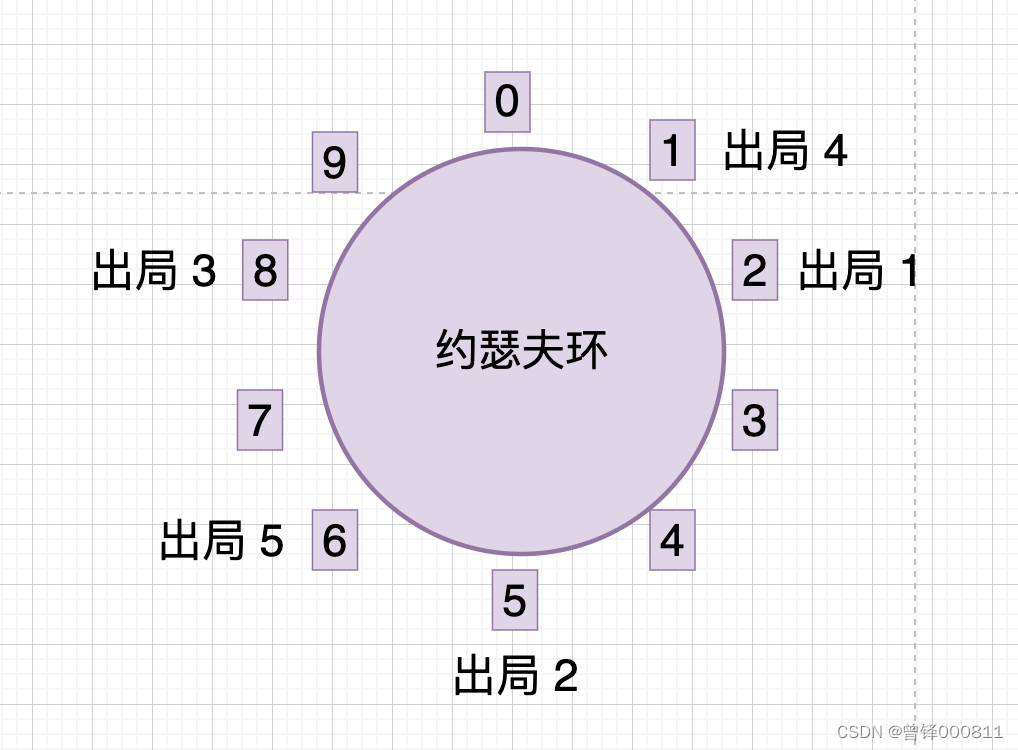
现在从编号为7的人开始报数，编号7的人报数为1 ，跳过已经出局的编号8，编号9的人报数为2，编号0的人报数为3，编号0的人出局： 

跳过已经出局的编号1和编号2， 现在从编号为3的人开始重新报数，编号3报数为1，编号4报数为2，跳过已经出局的编号5和编号6，编号7报数为3，编号7出局：

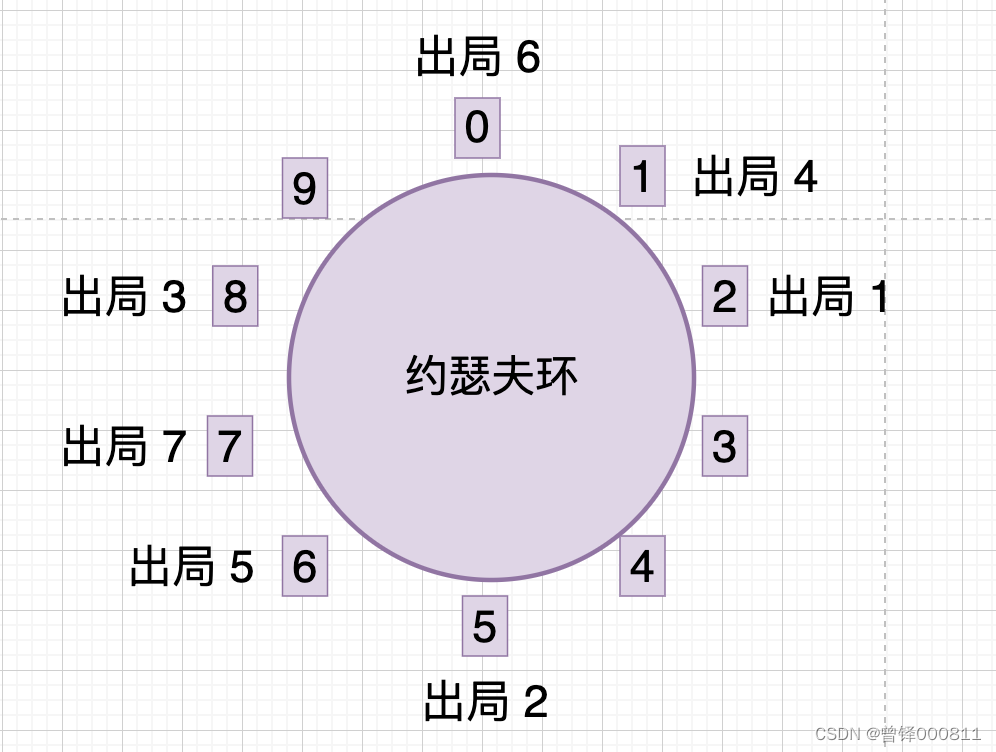
跳过已经出局的编号8， 从编号9开始报数，编号9报数为1，跳过已经出局的编号0、1、2， 编号3报数为2，编号4报数为3，现在编号为4的人出局：

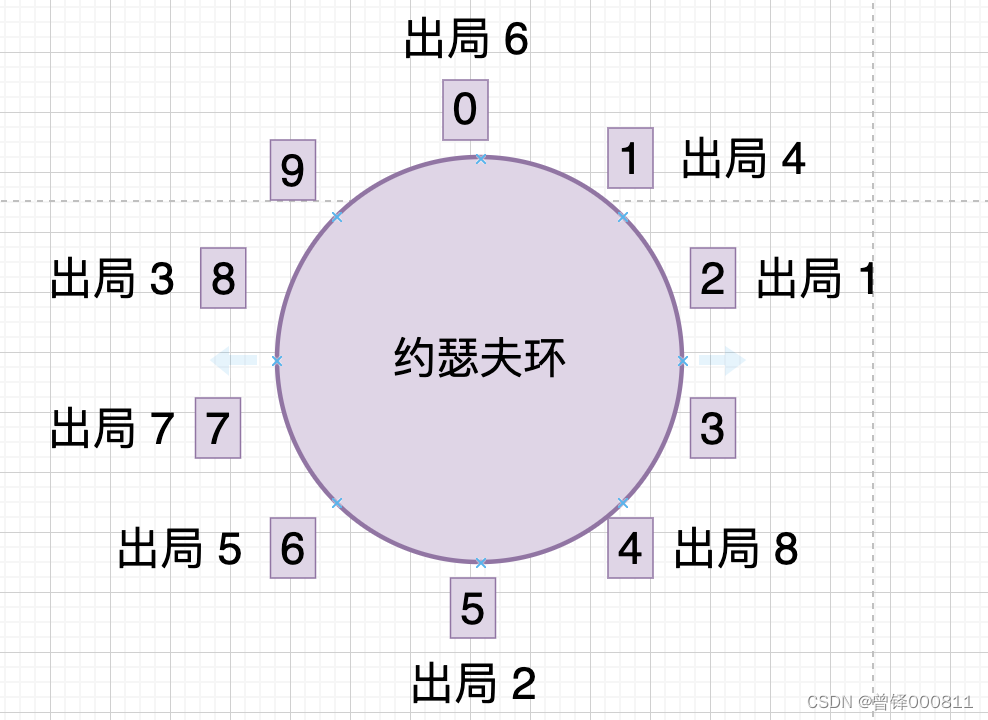
跳过已经出局的编号5、6、7、8，从编号9开始报数，编号9报数为1，跳过出局的编号0、1、2，编号3报数为2，跳过出局的编号4、5、6、7、8，编号9报数为3，编号9出局，此时约瑟夫环中只剩下编号为3的成员，所以最终的胜利者是编号为3的人：

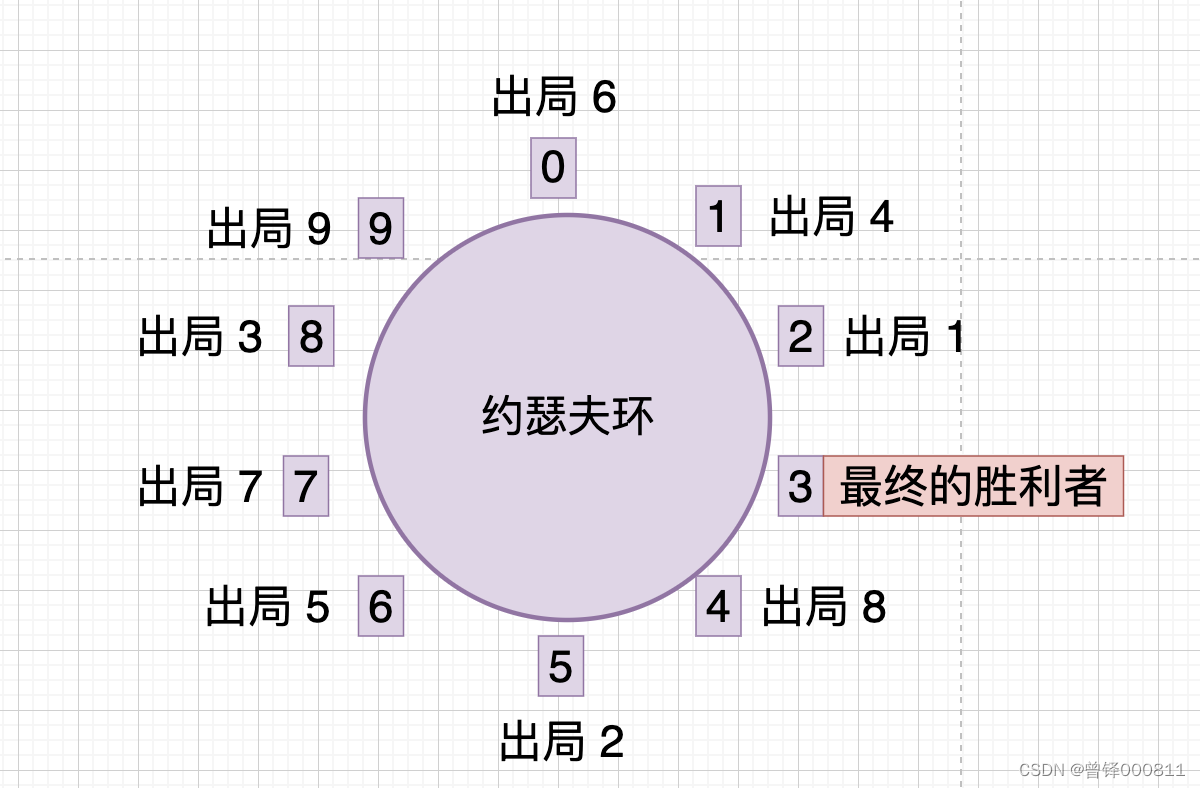
所以最终出局人编号的顺序为： 2，5，8，1，6，0，7，4，9，3，最后一个出局的人为最终的胜利者

约瑟夫环游戏的过程我们已经基本清楚，我们将思路代码化。

代码实现： 

方法一：数组

//利用数组来解决约瑟夫环
#include
#include
using namespace std;
int arr[100] = {0};//定义一个长度为100的数组且将数组内的元素全部初始化为0，0也表示一个人还在环中
int main()
{
    int n = 0,m = 0;//n表示总共的人数，m表示数到第m个人的时候出局
    int count = 0;//count用作记录出局人数的计数器
    int i = 0,k = 0;//定义两个下标，i用来表示目前报数的编号，k用来记录编号1到编号m的依次报数
    cin >> n >> m;//输入约瑟夫环内的总人数和需要出局的人的编号
    while(count != n){//循环跳出的条件为全部人数全部出局
        i++;//从第一个人往后走
        if(i > n){//如果超过总人数，重新从第一个人开始报数
            i = 1;
        }
        if(arr[i] == 0){//这个人还在环中的话
            k++;//报数操作，从1开始，k在下面归0
            if(k == m){//如果报数到了第m个数字
                arr[i] = 1;//重新将当前这个位置设置为1
                count++;//出局人数加1
                cout << i-1 << " ";//输出当前元素（下标形式）
                k = 0;//对k进行清空。重新从编号1开始报数
            }
        }
    }
    return 0;
}

我们利用程序对上面分析的过程以及结果进行验证：

如图， 我输入总人数为10，数到第3人时出局，出局顺序为：2，5，8，1，6，0，7，4，9，3，与上面分析的结果一样，结果正确。

方法二：递归

在我之前的这篇C语言-8月1日-递归与动态内存管理​​​​​​​文章中曾经说过，递归就是将大问题分解成逐层分解成能解决的小问题，然后再将能解决的小问题逐层进行合并，合并成原规模的问题。

在这里我们先对约瑟夫环问题进行分解，这里我采用直线线性表的方式，这样更加直观：

现在定义递归函数，Josephus(int n,int m,int i) 

递归函数形参：n表示约瑟夫环内的总人数，m表示报数报到第m个人出局，i表示第i个人出局的编号。

例如：n = 10 , 报数报到第3个人出列(m = 3)

第一次出局： Josephus(10,3,1)  = 2

第二次出局：Josephus(10,3,2)  = 5

 第三次出局：Josephus(10,3,3)  = 8

 我们这时将约瑟夫环内的元素缩减为9个，也就是最大编号为8，在保持m和i不变的情况下，Josephus(9,3,2)  = 5​​​​​​​，此时我们再将约瑟夫环内的元素缩减为8个，也就是最大编号为7，在保持m和i不变的情况下，Josephus(8,3,1)  = 2

此时不难得出规律：

Josephus(10,3,3)  = Josephus(9,3,2)  + 3

Josephus(9,3,2)  = Josephus(8,3,1)  +  3

所以我们可以得出规律：Josephus(n,m,i)  = Josephus(n - 1,m,i -1) + m 

我们画一个树状图来进行描述：

​​​​​​​

但是这是始终在旧环内的情况下我们找到的规律，如果我们将报数的值设置为6，情况又是如何呢？

第一次出局： Josephus(10,6,1)  = 5

第二次出局： Josephus(10,6,2)  = 1

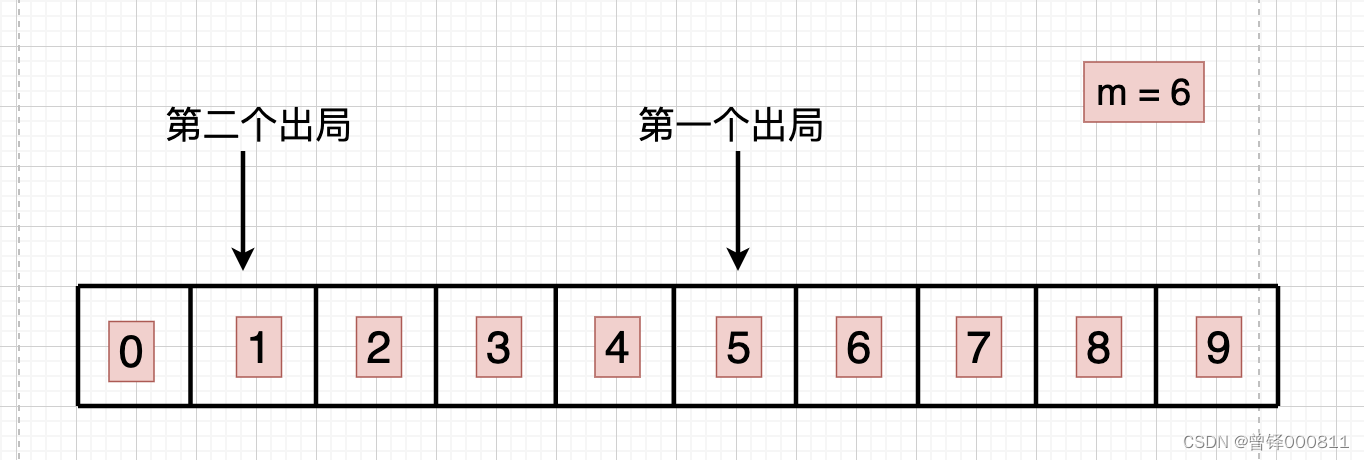
此时我们可以发现第一次出局的编号为5，第二次出局人的编号为1，1也就是(5 + 6) % 10，和上面的规律相似，我们可以得出以下规律：

Josephus(10,6,2) = [Josephus(9,6,1) + 6] % 10 = 1

所以我们可以得出规律：当不为第一个出局时（i != 1）：

[Josephus(n,m,i)  = Josephus(n - 1,m,i -1) + m] % n

当为第一个出局时（n = 1）:

 Josephus(n,m,i)  = (m - 1 + n) % n ,i = 1（递归出口）

规律我们已经清楚，现在将思路进行代码化。

代码实现：

方法二：递归：

#include
#include
using namespace std;
int Josephus(int n,int m,int i)
{
    if(i == 1){
        return (m - 1 + n) % n;
    }
    else{
        return (Josephus(n - 1 ,m,i - 1) + m) % n;
    }
}
int main()
{
    int n = 0,m = 0;
    cin >> n >> m;
    for(int i = 1;i <= n;i++){
        printf("第%d个出局: %d\n",i,Josephus(n,m,i));
    }
    return 0;
}

运行结果：

如图，出局的顺序依然是：2，5，8，1，6，0，7，4，9，3，编号为3的人是最终胜利者，结果正确。 

参考资料：

数组实现

递归实现