【计算机视觉】尺度不变特征变换(SIFT)

1. SIFT简介

• Sift（尺度不变特征变换Scale Invariant Feature Transform）：Sift提取图像的局部特征，在尺度空间寻找极值点，并提取出其位置、尺度、方向信息。

• Sfit的应用范围：物体辨别、机器人地图感知与导航、影像拼接、3D模型建立、手势识别、影像追踪等

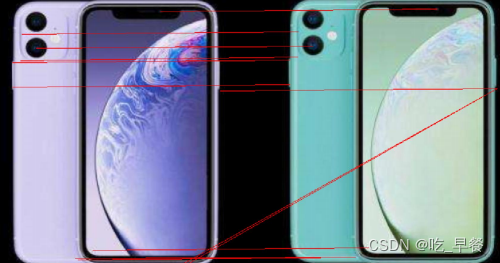
  分别提取待拼接图片的特征点、拟合透视矩阵得到不同场景下的同一物体

  

  将两个图片中的相似点进行连接

  

• Sift特征的特点

  • 对视角变化、噪声等也存在一定程度的稳定性；
  • 独特性，信息量丰富，适用于在海量特征数据中进行快速，准确的匹配；
  • 多量性，即使少数几个物体也可以产生大量的Sfit特征向量；

• Sfit算法实质：在不同的尺度空间上查找关键点（特征点），计算关键点的大小、方向、尺度信息，利用这些信息组成关键点对特征点进行描述的问题。Sift所查找的关键点都是一些十分突出，不会因光照，仿射变换和噪声等因素而变换的“稳定”特征点，如角点、边缘点、暗区的亮点以及亮区的暗点等。

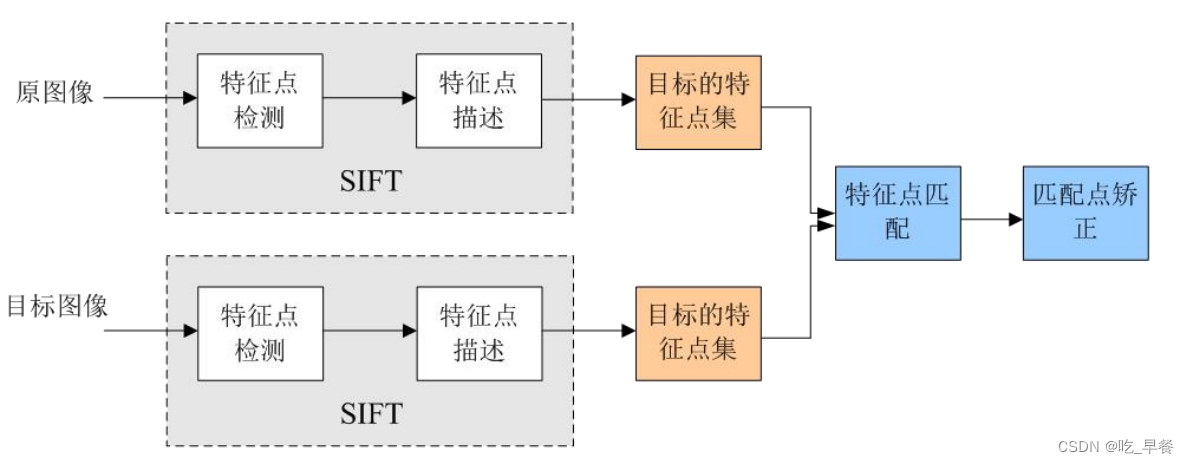
2. SIFT特征提取和匹配具体步骤

匹配的过程就是对比这些特征点的过程：

SIFT函数注册了专利，在商业用途上是收费的。将在opencv > 3.4.3中，不再提供。

解决办法： （先下载python3.6才能支持低版本的opencv）

conda create --name py3.6 python=3.6 #创建python3.6环境
conda activate py3.6 #进入该环境
pip install opencv-python==3.4.1.15 #安装opencv
pip install opencv-contrib-python==3.4.1.15 #安装opencv的其他包
1
2
3
4

SIFT特征提取和匹配具体步骤 如下6步

1. 生成高斯差分金字塔（DOG金字塔），尺度空间构建

2. 空间极值点检测（关键点的初步查探）

3. 稳定关键点的精确定位

4. 稳定关键点方向信息分配

5. 关键点描述

6. 特征点匹配

2.1 生成高斯差分金字塔 尺度空间构建

尺度空间与图像金字塔关系

• 尺度空间解释：试图在图像领域中模拟人眼观察物体的概念与方法。例如：观察一颗树，关键在于我们想要观察是树叶子还是整棵树：如果是一整棵树(相当于大尺度情况下观察)，那么就应该去除图像的细节部分。如果是树叶(小尺度情况下观察)，那么就该观察局部细节特征。
• 尺度空间：相当于一个图片需要获得多少分辨率的量级。
• 图像金字塔：如果把一个图片从原始分辨率不停的对其分辨率进行减少，然后将这些图片摞在一起，可以看成一个四棱锥的样式，这个东西就叫做图像金字塔。
• 图像金字塔解释：图像金字塔是一种以多分辨率来解释图像的结构，通过对原始图像进行多尺度像素采样的方式，生成N个不同分辨率的图像。把具有最高级别分辨率的图像放在底部，以金字塔形状排列，往上是一系列像素（尺寸）逐渐降低的图像，一直到金字塔的顶部只包含一个像素点的图像，这就构成了传统意义上的图像金字塔。
• 关系：尺度空间构建的基础是DOG金字塔，DOG金字塔构建的基础是高斯金字塔。

获得图像金字塔一般包括二个步骤：

1. 利用滤波器平滑图像 （高斯滤波） ——这一步主要是进行降噪

2. 对平滑图像进行抽样（采样）

有两种采样方式——上采样（分辨率逐级升高）和下采样（分辨率逐级降低）

2.1.1 高斯金字塔

• 主要思想：通过对原始图像进行尺度变换，获得图像多尺度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作为一种特征向量，实现边缘、角点检测不同分辨率上的关键点提取等。 各尺度下图像的模糊度逐渐变大，能够模拟人在距离目标由近到远时目标物体在视网膜上的形成过程。

• 注意：高斯金字塔是在SIFT中提出来的概念，首先高斯金字塔并不是一个金字塔，而是有很多组（Octave）金字塔构成，并且每组金字塔都包含若干层（Interval）。

• 高斯金字塔构建过程：

  1. 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层，将第1组第1层图像经高斯卷积（其实就是高斯平滑或称高斯滤波）之后作为第1组金字塔的第2层。

  2. 将σ乘以一个比例系数k，得到一个新的平滑因子σ=k*σ，用它来平滑第1组第2层图像，结果图像作为第3层。

  3. 如此这般重复，最后得到L层图像，在同一组中，每一层图像的尺寸都是一样的，只是平滑系数不一样。它们对应的平滑系数分别为：0，σ，kσ，k^2σ,k3σ……k^(L-2)σ。

  4. 将第1组倒数第三层图像作比例因子为2的降采样（比例因子为2也就是图片的尺寸减半），得到的图像作为第2组的第1层，然后对第2组的第1层图像做平滑因子为σ的高斯平滑，得到第2组的第2层，就像步骤2中一样，如此得到第2组的L层图像，同组内它们的尺寸是一样的，对应的平滑系数分别为：0，σ，kσ，k^2σ,k3σ……k^(L-2)σ。但是在尺寸方面第2组是第1组图像的一半。

  高斯卷积的公式如下：（其中σ一般取1.6为最佳）
  $$G(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{(x-x_0{)}^2+(y-y_0}{2{\sigma }^2}}$$