-
TinyRenderer学习笔记--Lesson 3、4
Lesson 3 zbuffer
无论怎样,生活中的显示器基本上都是平面,是一个2D的场景,而我们的模型却是3D的,是有深度的,实际上我们看见的都只是离我们的眼睛最近的那一个平面,一个不透明的3D物体的内部和背面是我们无法观测到的。对应到计算机里面,我们就需要知道一个物体哪个平面离我们的虚拟摄像机最近,但是这往往是很难办到的,如下:
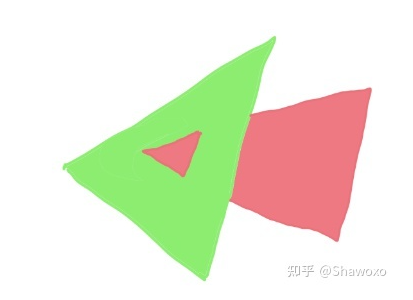
显然,我们无法判断绿色三角形和粉色三角形哪个离平面更近,这时就不能以三角形平面为单位来绘制,需要以像素为单位来绘制。
void triangle(Vec3f* pts, float* zbuffer, TGAImage& image, TGAColor color) { //定义包围盒 Vec2f bboxmin(std::numeric_limits::max(), std::numeric_limits ::max()); Vec2f bboxmax(-std::numeric_limits ::max(), -std::numeric_limits ::max()); Vec2f clamp(image.get_width() - 1, image.get_height() - 1); //找到包围盒 for (int i = 0; i < 3; ++i) { for (int j = 0; j < 2; ++j) { bboxmin[j] = std::max(0.f, std::min(bboxmin[j], pts[i][j])); bboxmax[j] = std::min(clamp[j], std::max(bboxmax[j],pts[i][j])); } } Vec3f p; for (p.x = bboxmin.x; p.x < bboxmax.x; p.x++) { for (p.y = bboxmin.y; p.y < bboxmax.y; p.y++) { //找到重心坐标并判断判断是否在三角形内 Vec3f bc_screen = barycentric(pts[0], pts[1], pts[2], p); if (bc_screen.x < 0 || bc_screen.y < 0 || bc_screen.z < 0) continue; p.z = 0; //通过重心坐标计算深度值 for (int i = 0; i < 3; i++) p.z += pts[i][2] * bc_screen[i]; if (zbuffer[int(p.x + p.y * width)] < p.z) { //更新深度值 zbuffer[int(p.x + p.y * width)] = p.z; image.set(p.x, p.y, color); } } } } ......... Vec3f light_dir(0, 0, -1); //深度缓冲区,并赋值 float* zbuffer = new float[width * height]; for (int i = width * height; i--; zbuffer[i] = -std::numeric_limits ::max()); for (int i = 0; i < model->nfaces(); i++) { std::vector face = model->face(i); Vec3f pts[3]; Vec3f world_coords[3]; for (int j = 0; j < 3; ++j) { Vec3f v = model->vert(face[j]); pts[j] = world2screen(model->vert(face[j])); world_coords[j] = v; } Vec3f n = cross((world_coords[2] - world_coords[0]),(world_coords[1] - world_coords[0])); n.normalize(); float intensity = n * light_dir;//光照强度=法向量*光照方向 即法向量和光照方向重合时,亮度最高 //强度小于0,说明平面朝向为内 即背面裁剪 if (intensity > 0) { triangle(pts,zbuffer, image, TGAColor(intensity * 255, intensity * 255, intensity * 255, 255)); } } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
在我们之前上一节实现的平面着色上增加深度值的检测,会让我们的图象看起来更加立体

下面将要给我们的模型加上贴图,让渲染的模型看起来更加真实。这里我们采用重心坐标插值的办法来进行纹理贴
图,首先我们需要知道某个三角形顶点上的UV值,然后通过插值的办法计算出三角形内部某个点的UV值,OBJ文
件里已经保存了顶点的纹理坐标和纹理信息,只需要进行一次插值计算即可。关键代码如下:
Vec3f p; for (p.x = bboxmin.x; p.x < bboxmax.x; p.x++) { for (p.y = bboxmin.y; p.y < bboxmax.y; p.y++) { //找到重心坐标并判断是否在三角形内 Vec3f bc_screen = barycentric(pts[0], pts[1], pts[2], p); if (bc_screen.x < 0 || bc_screen.y < 0 || bc_screen.z < 0) continue; p.z = 0; //重心坐标插值计算UV值 Vec2i uvp = uv[0] * bc_screen.x + uv[1] * bc_screen.y + uv[2] * bc_screen.z; //通过重心坐标计算深度值 for (int i = 0; i < 3; i++) p.z += pts[i][2] * bc_screen[i]; if (zbuffer[int(p.x + p.y * width)] < p.z) { //更新深度值 zbuffer[int(p.x + p.y * width)] = p.z; TGAColor color = model->diffuse(uvp); //找到对应纹理 image.set(p.x, p.y, TGAColor(color.r * intensity, color.g * intensity, color.b * intensity, 255)); } } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
if (intensity > 0) { Vec2i uv[3]; for (int k = 0; k < 3; k++) { uv[k] = model->uv(i, k);//获取三个顶点的UV值 } triangle(pts,zbuffer,uv, image,intensity); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
注意,这里要对model.h和geometry.h及.cpp文件进行修改,详情参考
效果如下:

Lesson 4 透视投影
投影大致可以分为透视投影和正交投影
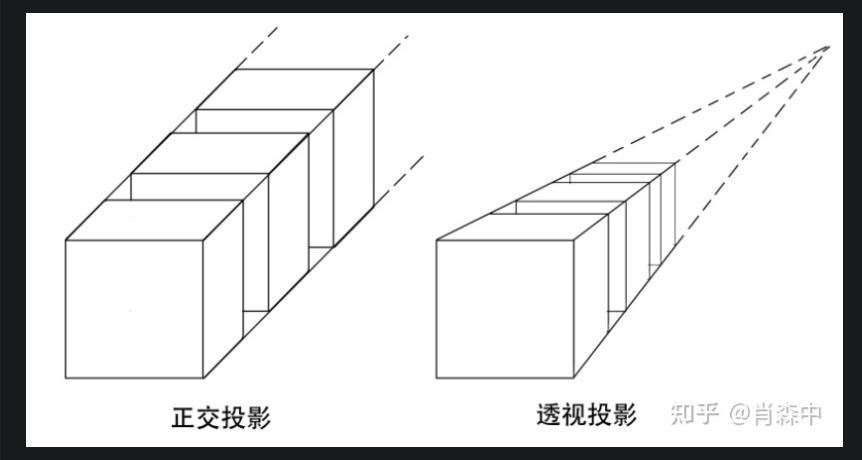
透视投影的最直观的效果就是近大远小。
对于透视投影的计算,我们需要进行简单的探讨,这里就不在讨论,强烈建议大家查看文章
文章中对缩放矩阵,平移矩阵等进行了详细的探讨。

其中 r = -1/c,
接下来就是进行编码了。代码大体上和上一节差不多,多的部分就是利用矩阵来实现透视投影。
两个功能函数,4D变3D和3D变4D,和一个视角转换函数,
Vec3f m2v(Matrix m) { return Vec3f(m[0][0] / m[3][0], m[1][0] / m[3][0], m[2][0] / m[3][0]); } Matrix v2m(Vec3f v) { Matrix m(4,1); m[0][0] = v.x; m[1][0] = v.y; m[2][0] = v.z; m[3][0] = 1.f;//添加一个1表示坐标 return m; } //视图矩阵,把模型坐标的(-1,1)转换成屏幕坐标的(100,700) //zbuffer从(-1,1)转换成0~255 Matrix viewport(int x, int y, int w, int h) { Matrix m = Matrix::identity(4); //平移 m[0][3] = x + w / 2.f; m[1][3] = y + h / 2.f; m[2][3] = depth / 2.f; //缩放 m[0][0] = w / 2.f; m[1][1] = h / 2.f; m[2][2] = depth / 2.f; return m; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
对投影矩阵和视角矩阵进行初始化,这里注意投影矩阵的[3] [2]坐标
//初始化透视投影矩阵 Matrix Projection = Matrix::identity(4); //初始化视角矩阵 Matrix ViewPort = viewport(width / 8, height / 8, width * 3 / 4, height * 3 / 4); //投影矩阵[3][2]=-1/c,c为相机z坐标 Projection[3][2] = -1.f / camera.z;- 1
- 2
- 3
- 4
- 5
- 6
有了这三个矩阵,在计算屏幕坐标的时候,直接进行乘就行,简称为MVP变换,M是模型矩阵,V是视角矩阵,P是投影矩阵。
for (int j = 0; j < 3; j++) { Vec3f v = model->vert(face[j]); //视角矩阵*投影矩阵*坐标 screen_coords[j] = m2v(ViewPort * Projection * v2m(v)); world_coords[j] = v; }- 1
- 2
- 3
- 4
- 5
- 6
就在这里应用,和原来的代码的主要不同之处也就在这。最后结果如下

下面是深度图:

现在通过学习,已经学会了
三角形的栅格化及背面剔除 (通过实现不同光照来实现背部剔除)
zbuffer深度缓冲区
纹理贴图 (利用重心坐标插值)
透视投影 (MVP变换)
之处也就在这。最后结果如下
-
相关阅读:
400Gbps 网络面临的挑战
Vue学习之--------绑定样式、条件渲染、v-show和v-if的区别(2022/7/12)
机试:成绩排名
稻米之缘农耕稻作文化 国稻种芯-万祥军:影响中国历史走向?
从零入门 Vite 与 Webpack 对比
c++ vector erase
【后端】HTTP3
实战Docker未授权访问提权
Excel·VBA单元格区域数据对比差异标记颜色
E.密码(算法选修)
- 原文地址:https://blog.csdn.net/qq_51599283/article/details/126604670
