国赛高教杯使用python/matlab必会基础数学建模-数据处理模块(课程4)

前言：我看有人的博客学习资料本就是基础知识然后还整个付费专栏博客，那我就直接打破这一垄断，直接上干货免费资料供大家学习。

国赛高教杯数据处理全过程总结

数据存在的问题

  ⚫ 数据预处理是数据挖掘中的重要一环，而且必不可少。要更有效地挖掘出知识，就必须为其提供干净，准确，简洁的数据。
  ⚫ 现实世界中数据常常是不完整，不一致的脏数据，无法直接进行数据挖掘，或挖掘结果差强人意。

原始数据存在的问题

  −数据的不一致：各系统间的数据存在较大的不一致性
如属性重量的单位：
  A数据库重量单位kg
  B数据库重量单位g
  −噪声数据：数据中存在着错误或异常（偏离期望值），如：血压和身高为0就是明显的错误。
  收集数据的时候难以得到精确的数据，主要原因：
  收集数据的设备可能出现故障；
  数据输入时可能出现错误；
  数据传输过程中可能出现错误；
  存储介质有可能出现损坏等。
  − 缺失值：由于实际系统设计时存在的缺陷以及使用过程中的一些人为因素，数据记录可能会出现数据值的丢失或不确定。
  − 原因可能有：
  ⚫ 有些属性的内容有时没有（家庭收入，参与销售事务数据中的顾客信息）；
  ⚫ 有些数据当时被认为是不必要的；
  ⚫ 由于误解或检测设备失灵导致相关数据没有记录下来；
  ⚫ 与其它记录内容不一致而被删除；
  ⚫ 忽略了历史数据或对数据的修改。
  数据质量要求
  ⚫ 准确性：数据记录的信息是否存在异常或错误。
  ⚫ 完整性：数据信息是否存在缺失。
  ⚫ 一致性：指数据是否遵循了统一的规范，数据集合是否  保持了统一的格式
  ⚫ 时效性：某些数据是否能及时更新
  ⚫ 可信性：用户信赖的数据的数量
  ⚫ 可解释性：指数据自身是否易于人们理解
  数据预处理的主要任务
  ⚫ 数据清理（清洗）：去掉数据中的噪声，纠正不一致。
  ⚫ 数据集成：将多个数据源合并成一致的数据存储，构成一个完整的数据集，如数据仓库。
  ⚫ 数据归约（消减）：通过聚集、删除冗余属性或聚类等方法来压缩数据。
  ⚫ 数据变换（转换）：将一种格式的数据转换为另一格式的数据(如规范化)。

数据清理

  数据清理就是对数据进行重新审查和校验的过程。其目的在于纠正存在的错误，并提供数据一致性。
  • 缺失值的处理；
  • 噪声数据；
  • 不一致数据。
  空缺值的处理
  – 引起空缺值的原因
  • 设备异常
  • 与其他已有数据不一致而被删除
  • 因为误解而没有被输入的数据
  • 在输入时，有些数据因为得不到重视而没有被输入
  • 对数据的改变没有进行日志记载
  – 空缺值要经过推断而补上
  如何处理空缺值？
  1）忽略元组：
  • 若一条记录中有属性值被遗漏了，则将该记录排除在数据挖掘之外
  • 但是，当某类属性的空缺值所占百分比很大时，直接忽略元组会使挖掘性能变得非常差
  2）忽略属性列：
  • 若某个属性的缺失值太多，则在整个数据集中可以忽略该属性
  3）人工填写空缺值：
  • 工作量大，可行性低
  4）使用属性的中心度量值填充空缺值：
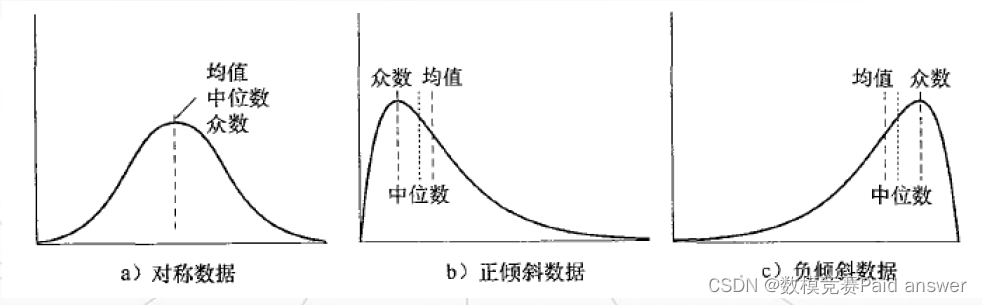
  • 如果数据的分布是正常的，就可以使用均值来填充缺失值
  • 如果数据的分布是倾斜的，可以使用中位数来填充缺失值。

  5）使用一个全局变量填充空缺值：
  • 对一个所有属性的所有缺失值都使用一个固定的值来填补（如“Not sure”或∞）。
  6）使用可能的特征值来替换空缺值（最常用）：
  • 生成一个预测模型，来预测每个丢失值
  • 如可以利用回归、贝叶斯计算公式或判定树归纳确定，推断出该条记录特定属性最大可能的取值

噪声的处理

  –噪声(noise) ：被测量的变量产生的随机错误或误差
  • 数据收集工具的问题
  • 数据输入错误
  • 数据传输错误
  • 技术限制
  • 命名规则的不一致
  如何检测噪声数据？
  1）基于统计的技术
  • 使用距离度量值（如马氏距离）来实现。
  • 给定p维数据集中的n个观察值𝑥𝑖（其中n>>p），用

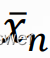
  表示样本平均向量，𝑉𝑛表示样本协方差矩阵，其中：

  2）基于距离的技术
  • 计算n维数据集中所有样本间的测量距离。
  • 如果样本S中至少有一部分数量为p的样本到𝑠𝑖的距离比d大，那么
样本𝑠𝑖就是数据集S中的一个噪声数据。
  例：基于距离的噪声检测方法

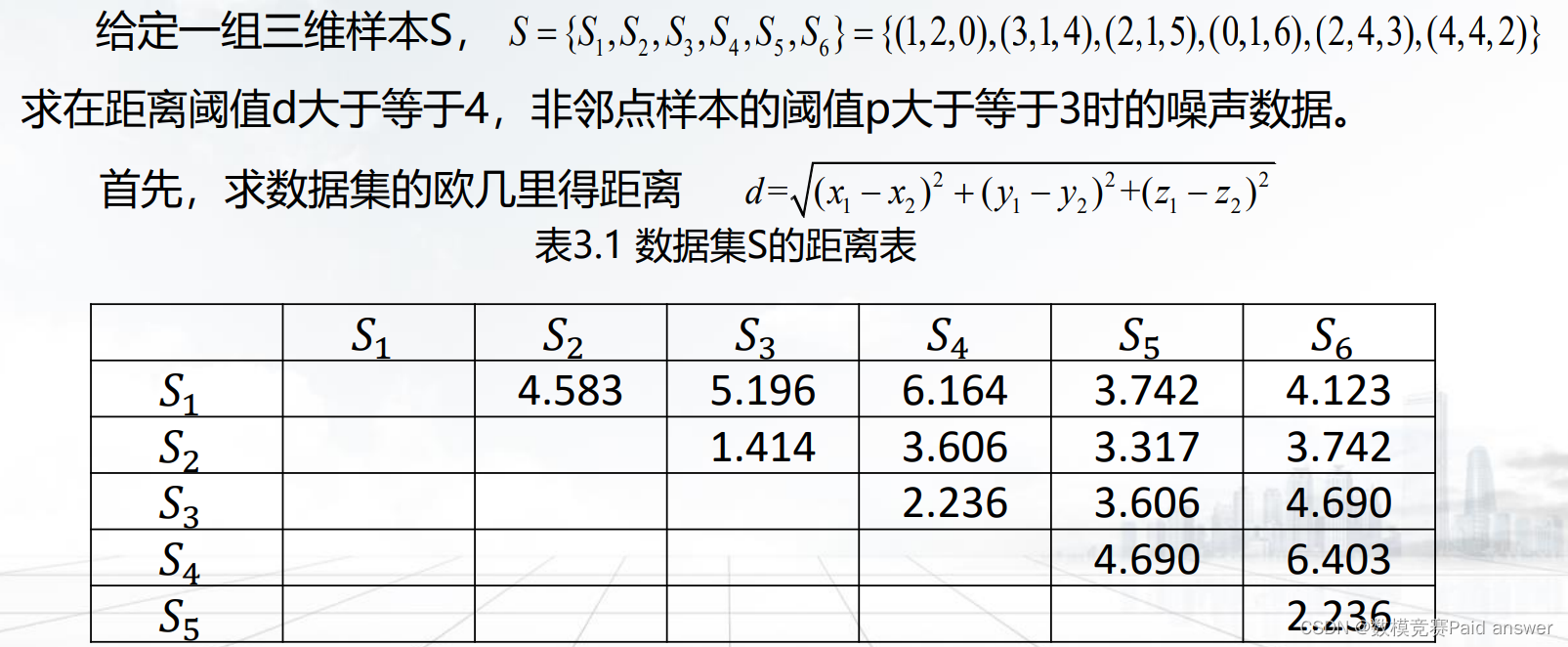
  然后根据阈值距离d=4，计算出每个样本p的值，即距离大于等于d的样本数量

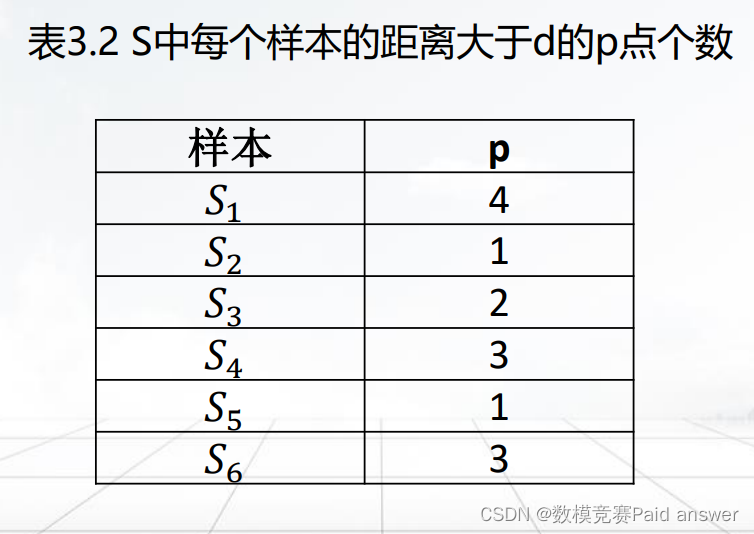
不一致数据的处理

  • 数据的不一致性，就是指各类数据的矛盾性、不相容性
  • 数据库系统都会有一些相应的措施来解决并保护数据库的一致性，可以使用数据库系统来保护数据的一致。

数据集成

  – 数据集成
  • 把不同来源、格式、特点和性质的数据合理地集中并合并起来。
  • 这些数据源可以是关系型数据库、数据立方体或一般文件。
  – 它需要统一原始数据中的所有矛盾之处，如字段的
  • 同名异义；
  • 异名同义；
  • 单位不统一；
  • 字长不一致等。
  – 集成过程中需要注意的问题：
  • 集成的过程中涉及的实体识别问题；
  • 冗余问题。

集成的过程中涉及的实体识别：

  – 整合不同数据源中的元数据；
  – 进行实体识别：匹配来自不同数据源的现实世界的实体；
  • 如：如何确定一个数据库中的brand和另一个数据库中的product是同一实体。
  • 通常，数据库的数据字典和数据仓库的元数据，可帮助避免模式集成中的错误。

冗余问题

  – 同一属性在不同的数据库或同一数据库的不同数据表中会有不同的字段名；
  – 一个属性可以由另外的属性导出，如：一个顾客数据表中的平均月收入属性，可以根据月收入属性计算出来。
  检测冗余的方法：
  – 相关性分析

  – 数值属性：采用相关系数和协方差进行相关性分析


  – 相关系数实例

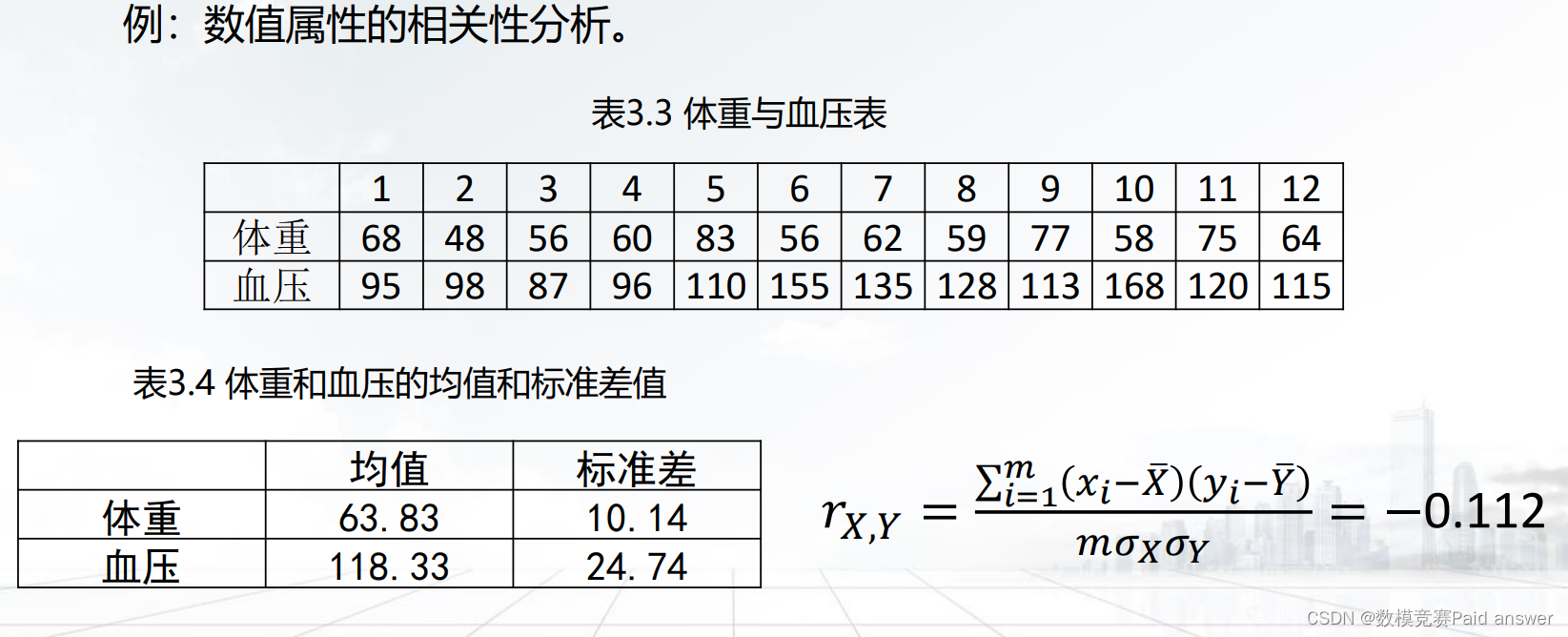
  – 数值属性：采用协方差进行相关性分析




  – 标称属性：使用卡方检验进行相关性分析




  – 卡方检验实例：二分类情况
  例：对从事两种工种的某一年龄段男性患某种疾病的情况进行调查，如下表。分析某一年龄段男性患某种疾病与从事工种是否相关。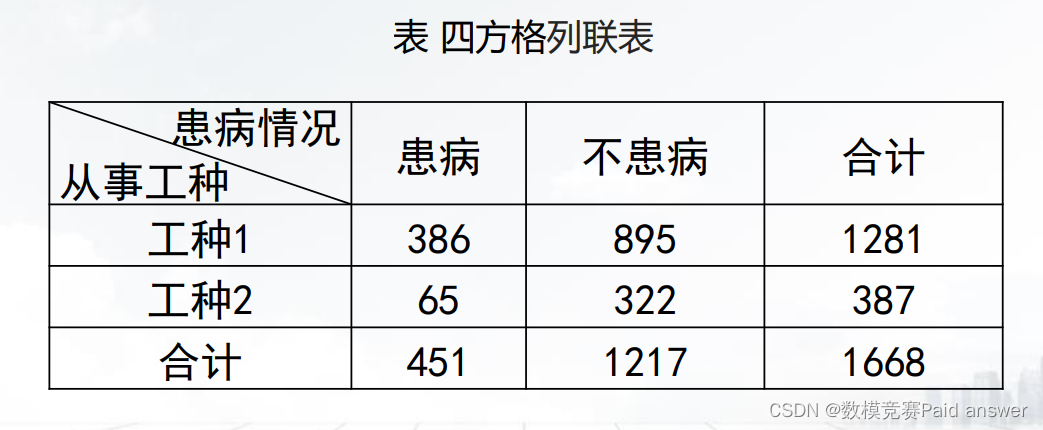

  （1）统计假设：
  H0：某一年龄段男性患某种疾病与从事工种不相关
  （2）期望频数的计算。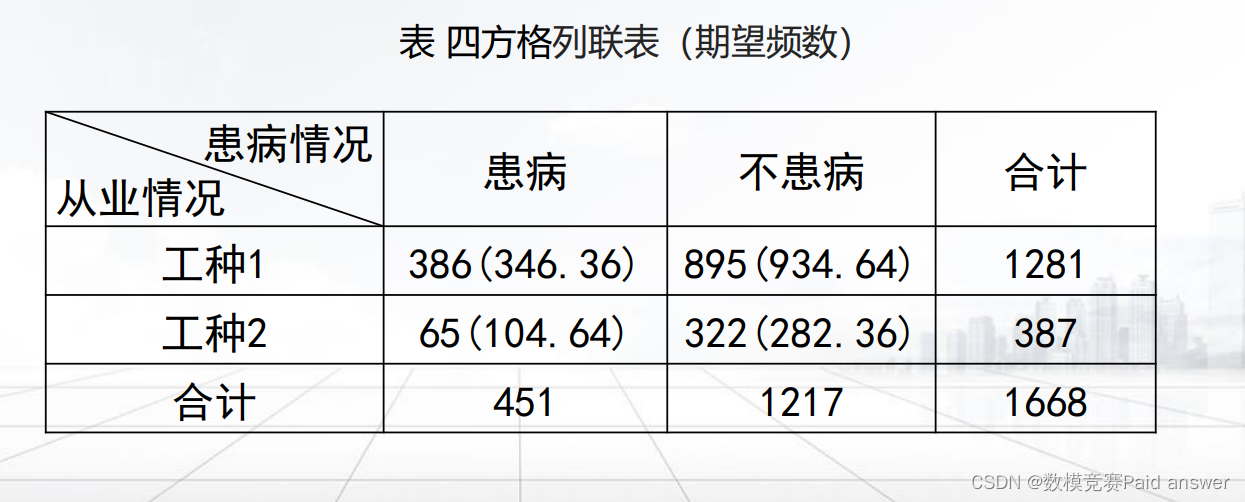

  （3）自由度的确定：df=（2-1）*（2-1）=1
  （4）卡方统计量的计算

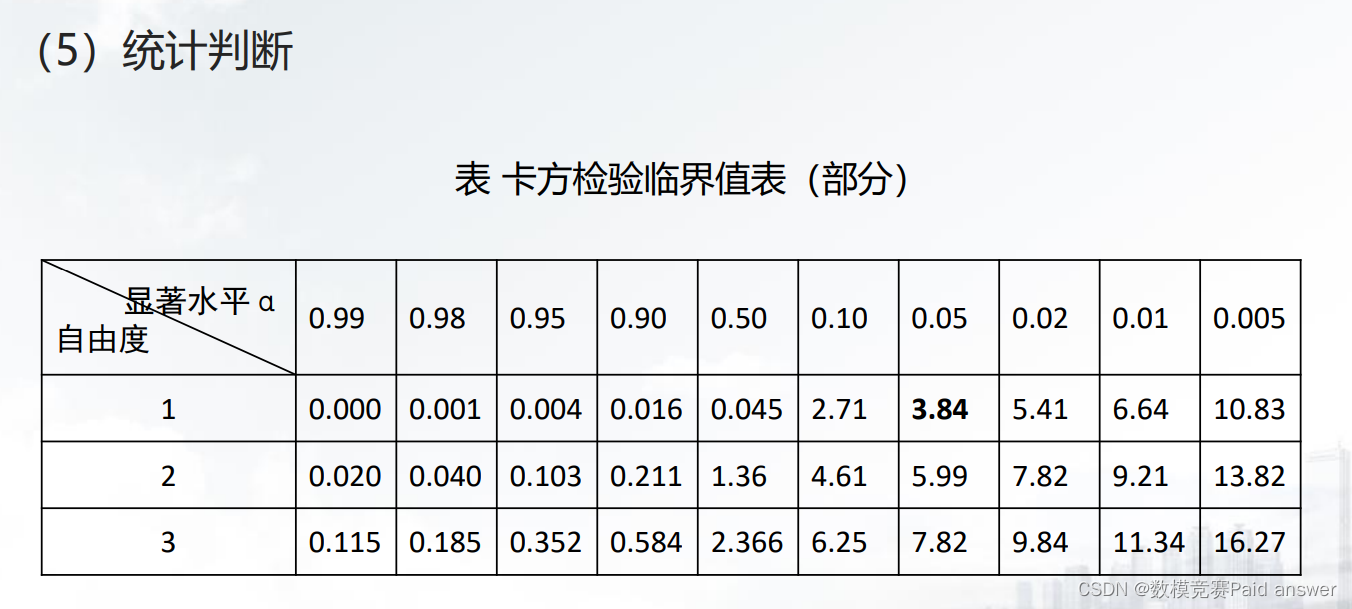
数据归约

  • 对大规模数据库内容进行复杂的数据分析常需要消耗大量的时间，使得这样的分析变得不现实和不可行；
  • 数据归约（data reduction）：数据消减或约简，是在不影响最终挖掘结果的前提下，缩小所挖掘数据的规模；
  • 数据归约技术可以用来得到数据集的归约表示，它小得多，但仍接近保持原数据的完整性；
  • 对归约后的数据集进行挖掘可提高挖掘的效率，并产生相同（或几乎相同）的结果。
  ‒ 数据归约的标准：
  • 用于数据归约的时间不应当超过或“抵消”在归约后的数据集上挖掘节省的时间。
  • 归约得到的数据比原数据小得多，但可以产生相同或几乎相同的分析结果。
  ‒ 数量归约：直方图
  • 直方图（Histogram）是一种常见的数据归约的形式。属性X的直方图将X的数据分布划分为不相交的子集或桶。通常情况下，子集或桶表示给定属性的一个连续区间。单值桶表示每个桶只代表单个属性值/频率对（单值桶对于存放那些高频率的离群点，非常有效）
  • 划分桶和属性值的方法有两种：
  ①等宽：在等宽直方图中，每个桶的宽度区间是一致的。
  ②等频（或等深）：在等频直方图中，每个桶的频率粗略地计为常数，即每个桶大致包含相同个数的邻近数据样本
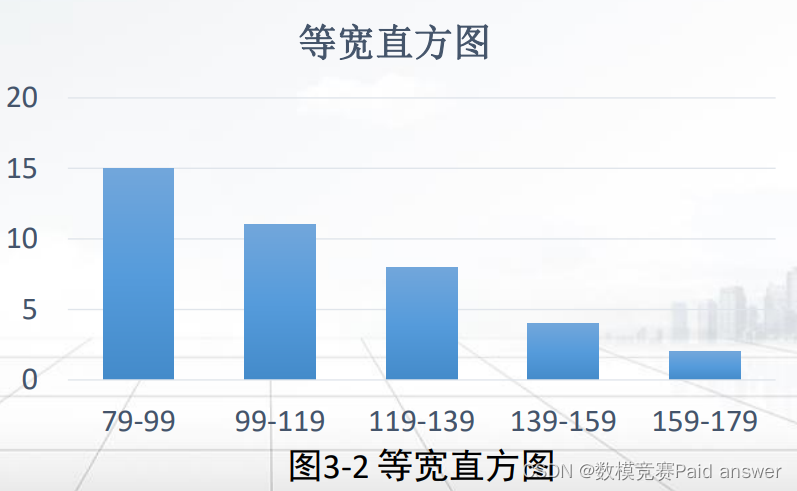
  例：用直方图表示数据
  已知某人在不同时刻下所量血压值为：95，98，87，96，110，155，135，128，113，168，120，115，110，155，135，128，113，158，87，96，110，98，87，94，80，93，89，95，99，101，111，123，128，113，158，128，113，168，87，96，110。使用等宽直方图表示数据，如图所示。由于需要继续压缩数据，所以一般都是使用桶来表示某个属性的一个连续值域。

  ‒ 数量归约：数据立方体
  • 数据立方体是一类多维矩阵，可以使用户从多个角度探索和分析数据集，它的数据是已经处理过的，并且聚合成了立方形式。
  • 数据立方体的基本概念。
  ①方体：不同层创建的数据立方体。
  ②基本方体：最低抽象层创建的立方体。
  ③顶方体：最高层抽象的立方体。
  ④方体的格：每一个数据立方体。


  ‒ 数据归约—属性子集选择：检测并删除不相关、弱相关或冗余的属性。
  属性子集选择的基本启发式方法包括逐步向前选择、逐步向后删除、逐步向前选择和逐步向后删除的组合以及决策树归纳，表3.7给出了属性子集选择方法。

  ‒ 数据归约—抽样
  • 允许用数据的较小随机样本（子集）表示大的数据集。
  • 取样方法：
  ➢ 不放回简单随机取样 （Simple Random Sampling Without Replacement, SRSWOR）
  ➢ 放回简单随机取样（Simple Random Sampling With Replacement, SRSWR）
  ➢ 聚类取样（Clustered Sampling）
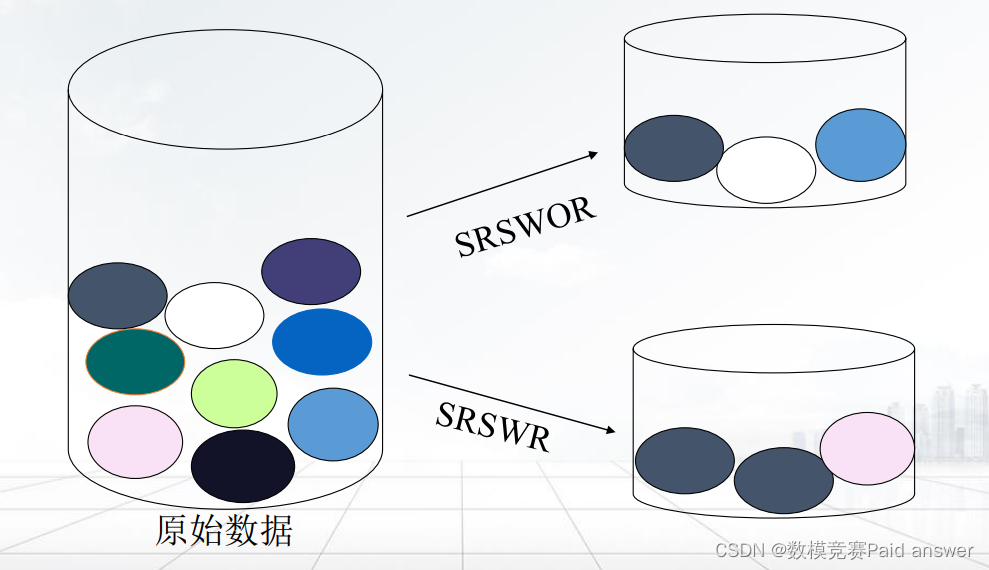
  ➢ 分层取样（Stratified Sampling）

  ‒ 数据归约—无放回简单随机取样（SRSWOR）& 放回简单随机取样（ SRSWR）

  • 假定大型数据集D包含N个元组
  • 无放回的简单随机抽样方法，从N个元组中随机（每一数据行被选中的概率为1/𝑁）抽取出n个元组，以构成抽样数据子集。
  • 有放回的简单随机抽样方法，与无放回简单随机抽样方法类似，也是从N个元组中每次抽取一个元组，但是抽中的元组接着放回原来的数据集D中，以构成抽样数据子集。这种方法可能会产生相同的元组。

  ‒ 数量规约-聚类采样：
  首先将大数据集D划分为M个互不相交的聚类，然后再从M个类中的数据对象分别进行随机抽取，可最终获得聚类采样的数据子集。

  ‒ 数量规约-分层取样：
  • 首先将大数据集D划分为互不相交的层，然后对每一层简单随机选样得到D的分层选样。
  • 如，根据顾客的年龄组进行分层，然后再在每个年龄组中进行随机选样，从而确保了最终获得分层采样数据子集中的年龄分布具有代表性。

数据变换与数据离散化

  数据变换：将数据转换成适合数据挖掘的形式
  -平滑：去掉数据中的噪声，将连续的数据离散化
  • 分箱
  • 回归
  • 聚类
  - 聚集：对数据进行汇总和聚集
  • avg(), count(), sum(), min(), max(),…
  • 如，每天销售额（数据）可以进行聚集操作以获得每月或每年的总额
  • 可用来构造数据立方体
  -数据泛化：使用概念分层，用更抽象（更高层次）的概念来取代低层次或
数据层的数据对象
  •如：街道属性，可以泛化到更高层次的概念，如城市、国家；
  •同样，对于数值型的属性，如年龄属性，可以映射到更高层次的概念，如年轻、中年和老年。

  -规范化：把属性数据按比例缩放，使之落入一个特定的小区间
  -属性构造：通过已知的属性构建出新的属性，然后放入属性集中，有助于挖掘过程。
  -离散化：数值属性的原始值用区间标签或概念标签替换。

  –数据变换：数据泛化——概念分层
  •概念分层定义了一组由低层概念到高层概念集的映射。允许在各种抽象级别上处理数据，从而在多个抽象层上发现知识。
  •用较高层概念替换低层次的概念，以此来减少取值个数。
  •概念分层结构可以用树来表示，树的每个节点代表一个概念。
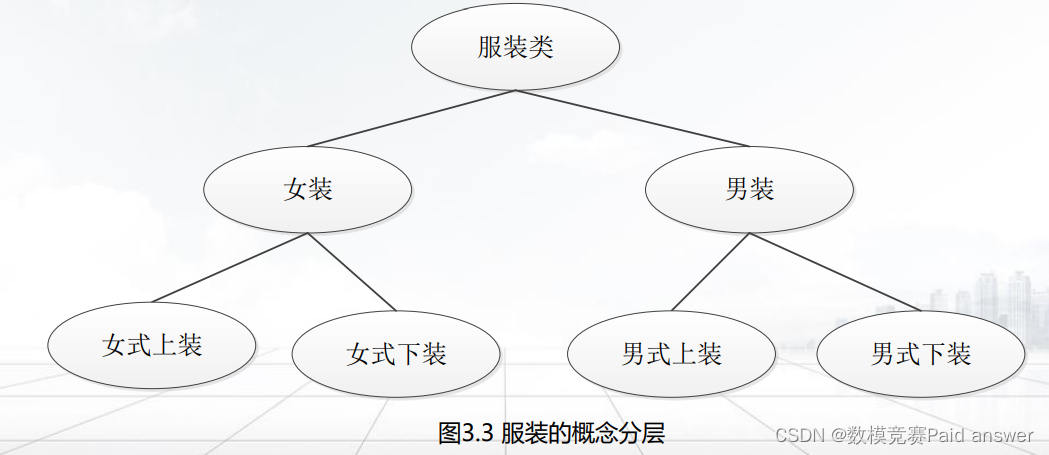
  例3.5 根据每个属性的不同值的个数产生概念分层。服装类的级别可以分为男装和女装，然后接下去可以分为上装和下装。服装的概念分层可以自动产生，如图3.3所示。

数据变换：规范化

  将数据按比例进行缩放，使之落入一个特定的区域，以消除数值型属性因大小不一而造成的挖掘结果的偏差。
  如将工资收入属性值映射到[-1.0, 1.0]的范围内
  – 规范化的目的：
  •将一个属性取值范围影射到一个特定范围之内，以消除数值性属性因大小不一而造成挖掘结果的偏差。
  – 常用的方法：
  小数定标规范化；
  最小-最大规范化；
  零-均值规范化（z-score规范化）。



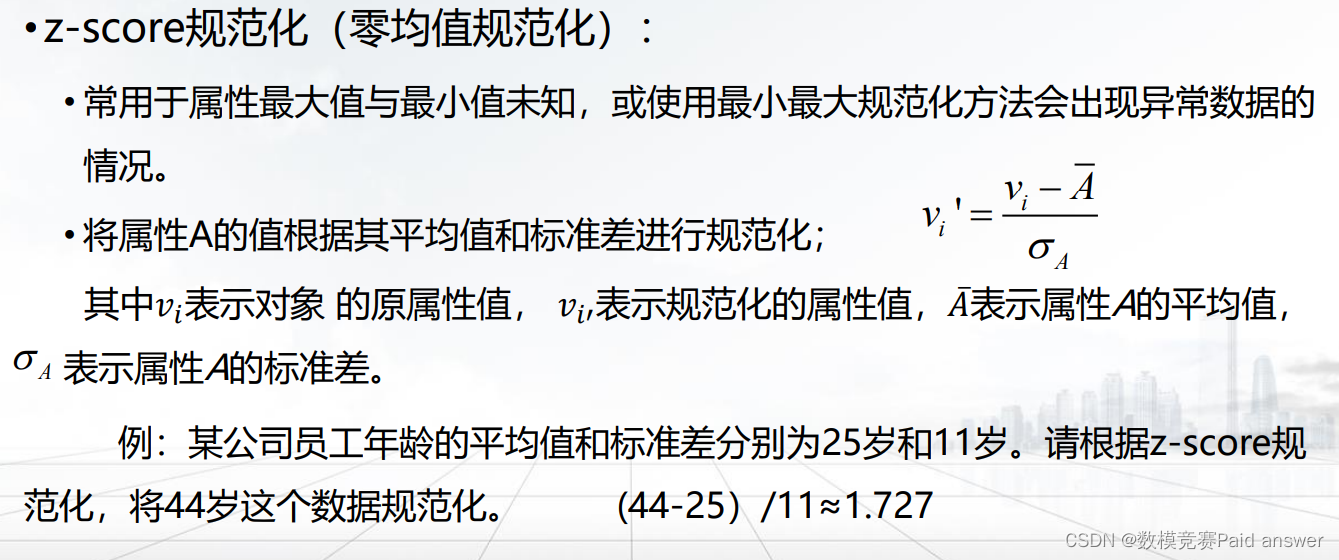
  注意：
  • 规范化将原来的数据改变很多，特别是上述的后两种方法。
  • 有必要保留规范化参数（如平均值和标准差，如果使用z-score规范化）以便将来的数据可以用一致的方式规范化。

  数据变换：属性构造
  •利用已有属性集构造出新的属性，并加入到现有属性集中以帮助挖掘更深层次的模式知识，提高挖掘结果的准确性；
  •如，根据宽、高属性，可以构造一个新属性：面积。
– 数据变换：离散化
  •连续变量的离散化，就是将具体性的问题抽象为概括性的问题，即是将它取值的连续区间划分为小的区间，再将每个小区间重新定义为一个唯一的取值。

  数据离散化的基本方法主要有分箱法和直方图分析法。
  对连续变量进行离散化处理，一般经过以下步骤：
  ①对此变量进行排序。
  ②选择某个点作为候选断点，根据给定的要求，判断此断点是否满足要求。
  ③若候选断点满足离散化的要求，则对数据集进行分裂或合并，再选择下一个候选断点。
  ④重复步骤②和③，如果满足停止准则，则不再进行离散化过程，从而得到最终的离散结果。
  数据离散化—分箱
  分箱的步骤：
  – 首先排序数据，并将它们分到等深（等宽）的箱中；
  – 然后可以按箱的平均值、或中值或者边界值等进行平滑。
  • 按箱的平均值平滑：箱中每一个值被箱中的平均值替换
  • 按箱的中值平滑：箱中的每一个值被箱中的中值替换
  • 按箱的边界平滑：箱中的最大和最小值被视为箱边界，箱中的
  每一个值被最近的边界值替换
  ① 等深分箱:
  •按记录数进行分箱，每箱具有相同的记录数，每箱的记录数称为箱的权重，也称箱子的深度。
  例3.6 分箱法。
  某公司存储员工信息的数据库里表示收入的字段“income”排序后的值（人民币元）：900，1000，1300，1600，1600，1900，2000，2400，2600，2900，3000，3600，4000，4600，4900，5000，请按照等深分箱法分箱。设定权重（箱子深度）为4，分箱后
            箱1：900，1000，1300，1600
            箱2：1600，1900，2000，2400
            箱3：2600，2900，3000，3600
            箱4：4000，4600，4900，5000
  用平均值平滑结果为：
            箱1：1200，1200，1200，1200
            箱2：1975，1975，1975，1975
            箱3：3025，3025，3025，3025
            箱4：4625，4625，4625，4625
  ②等宽分箱 (binning):
  • 在整个属性值的区间上平均分布，即每个箱的区间范围设定为一个常量，称为箱子的宽度。上例中设定区间范围（箱子宽度）为1000元人民币，按等宽分箱法分箱后
            箱1：900，1000，1300，1600，1600，1900
            箱2：2000，2400，2600，2900，3000
            箱3：3600，4000，4600
            箱4：4900，5000
  用平均值平滑结果为：
            箱1：1383，1383，1383，1383，1383，1383
            箱2：2580，2580，2580，2580，2580
            箱3：4067，4067，4067
            箱4：4950，4950
  数据离散化—直方图分析法:
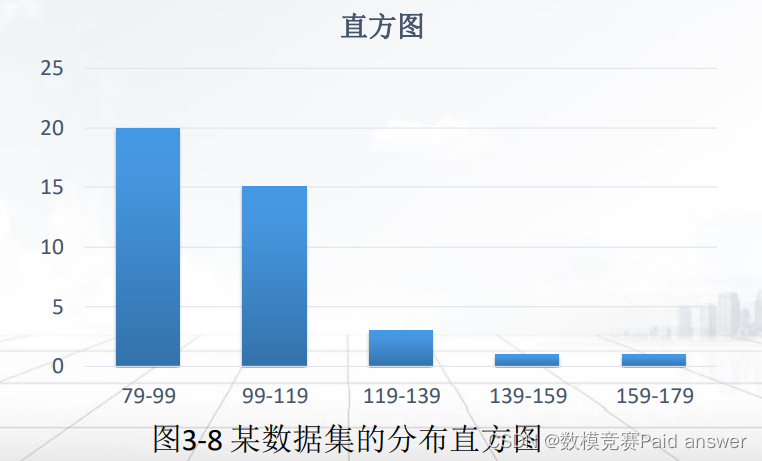
  直方图也可以用于数据离散化。它能够递归的用于每一部分，可以自动产生多级概念分层，直到满足用户需求的层次水平后结束。数据离散化—直方图分析法
  • 例如，图3-8是某数据集的分布直方图，被划分成了范围相等的区间（79至99，99至119，……，159至179）。这就产生了多级概念分层。