堆排序

• 堆
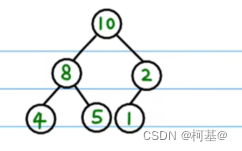
  它是数据结构的一种，特点：首先它是一棵完全二叉树，其次 父节点的值 > 子节点的值 ，例如下图
  

---

• 堆的表示
  从上往下，从左到右标号，用一个数组来表示 int arr[]={10,5,8,3,4,6,7,1,2}; ，这样表示还有一个好处，便是可以快速找寻某点的父节点与子结点，parent = (i-1)/2 , child_1=2i+1,child_2=2i+2 ，其中 i 为某点的下标
  

---

• 代码🖱️

void swap(int arr[], int i, int j) {    //交换函数
	int temp = arr[i];
	arr[i] = arr[j];
	arr[j] = temp;
}

void heapify(int tree[],int n,int i) {     //此函数的目的在于将完全二叉树树变为堆

	if (i >= n) {               // i 作为下标范围是 0 ~ n-1 ,超过这个范围即退出
		return ;
	}
	
	int max = i;   //假设当前结点的值是它以及它的左右孩子结点中的最大值，并用 max 记录当前结点的下标
	int c1 = 2 * i + 1;        // c1 为当前结点的左孩子结点的下标
	int c2 = 2 * i + 2;        // c2 为当前结点的右孩子结点的下标
	
	if (c1<n && tree[c1] > tree[max]) {    //如果当前结点的左孩子的值大于大于当前结点的值
		max = c1;                          // max 便指向当前结点左孩子的下标		
	}
	if (c2<n && tree[c2] > tree[max]) {    //如果当前结点的右孩子的值大于大于当前结点的值
		max = c2;                          // max 便指向当前结点右孩子的下标	
	}
	if (max != i) {                        //如果三个结点中的最大值不是当前结点的下标
		swap(tree, max, i);                //将当前结点的值与最大值结点的值互换
		heapify(tree, n, max);             //递归，继续向下执行上述操作
	}

}

void build_heap(int tree[],int n) {
	int last_node = n - 1;              //完全二叉树中最后一个结点的下标
	int parent = (last_node - 1) / 2;   //完全二叉树中最后一个结点的父节点的下标
	for (int i = parent; i >= 0; i--) {   //循环，从第一个父节点执行 heapify 操作，直到最后一个父节点即下标为 0 的结点
		heapify(tree, n, i);
	}
}

void heap_sort(int tree[],int n) {       //堆排序，调用了以上三个函数
	build_heap(tree, n);                
	for (int i = n - 1; i >= 0; i--) {
		swap(tree, i, 0);
		heapify(tree, i, 0);
	}

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

---

• 复杂度
  时间复杂度：O(nlog₂n)
  空间复杂度：O(1)

---

• 实践

#include
void swap(int arr[], int i, int j);
void heapify(int tree[], int n, int i);
void build_heap(int tree[], int n);
void heap_sort(int tree[], int n);

int main() {
	int tree[] = { 10,12,4,11,3,5,17,18 };
	int n = 6;
	heap_sort(tree, n);

	for (int i = 0; i < n; i++) {
		printf("%d,", tree[i]);
	}
	return 0;
}

void swap(int arr[], int i, int j) {
	int temp = arr[i];
	arr[i] = arr[j];
	arr[j] = temp;
}

void heapify(int tree[], int n, int i) {
	if (i >= n)
		return;
	int c1 = 2 * i + 1;                        //根结点的左孩子
	int c2 = 2 * i + 2;                        //根结点的左孩子
	int max = i;                           //假设根节点的下标为最大值的下标
	if (c1<n && tree[c1]>tree[max]) {      //左孩子的值大于根节点的值
		max = c1;                          //最大值的下标变成左孩子的下标
	}
	if (c2<n && tree[c2]>tree[max]) {      //右孩子的值大于根节点的值
		max = c2;                          //最大值的下标变成右孩子的下标
	}
	if (max != i) {                          //根节点的下标不是最大值的下标
		swap(tree, max, i);                  //互换
		heapify(tree, n, max);
	}
}

void build_heap(int tree[], int n) {
	int last_node = n - 1;
	int parent = (last_node - 1) / 2;
	int i;
	for (i = parent; i >= 0; i--) {
		heapify(tree, n, i);
	}

}

void heap_sort(int tree[],int n) {
	build_heap(tree, n);
	for (int i = n - 1; i >= 0; i--) {
		swap(tree, i, 0);
		heapify(tree, i, 0);
	}

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

运行结果：