• 数字逻辑设计（1）

    文章目录

    数字逻辑设计（1）

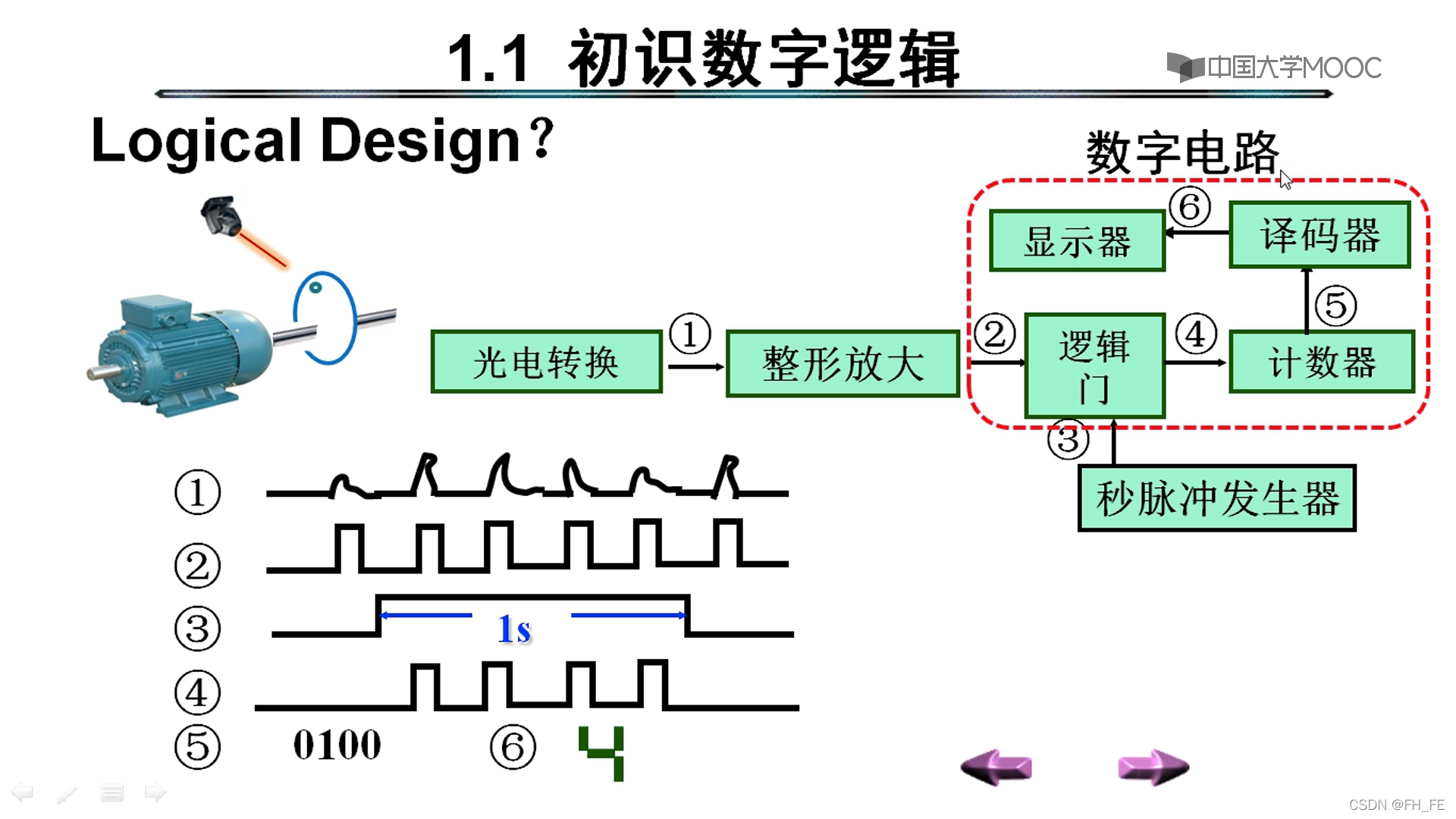
    在这里插入图片描述

    1. 初识数字电路

    在这里插入图片描述

    以获取电机转速为例：
    先通过光电转换出一个波形，将其整型放大
    利用逻辑门将整型放大后的规则的波形与秒脉冲器相与，得到了我们需要的能够代表速度的波形（即每秒的产生的波形数）
    通过计数器获取每秒产生的二进制波形数
    利用译码器将二进制数转化为十进制显示在显示器上

    红框内的电路设计部分属于数字逻辑设计范畴，而其余属于模拟电路

    数字逻辑设计分为三个部分：

    1. 系统设计： 将一个大的系统划分为多个子系统
    2. 逻辑设计： 通过设计逻辑运算实现各个子系统
    3. 电路设计： 利用基本的电子器件实现逻辑设计的功能

    模拟信号： 在时间上连续
    数字信号： 在时间上离散

    数字系统使用的是只有两种状态的二极管或三极管等开关器件
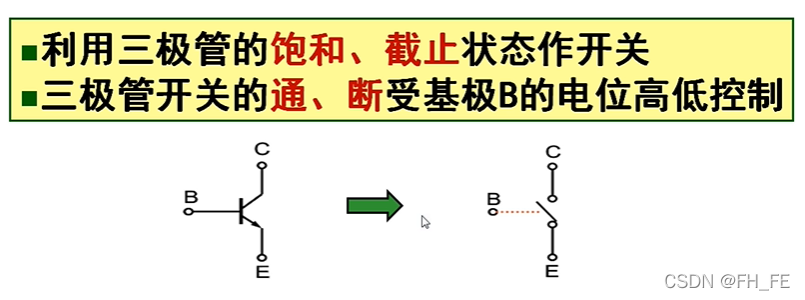
    在这里插入图片描述

    三极管高电压导通

    高电平 1
    低电平 0

    开关断开 0
    开关闭合 1

    2. 二进制编码

    二进制编码： 0和1在不同编码规则下的组合

    2.1 BCD码

    用四位二进制代表一位十进制数

    分类

    8421BCD 从高位到低位的权值为 8 4 2 1
    2421BCD
    4421BCD
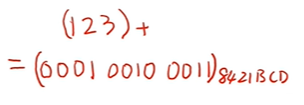
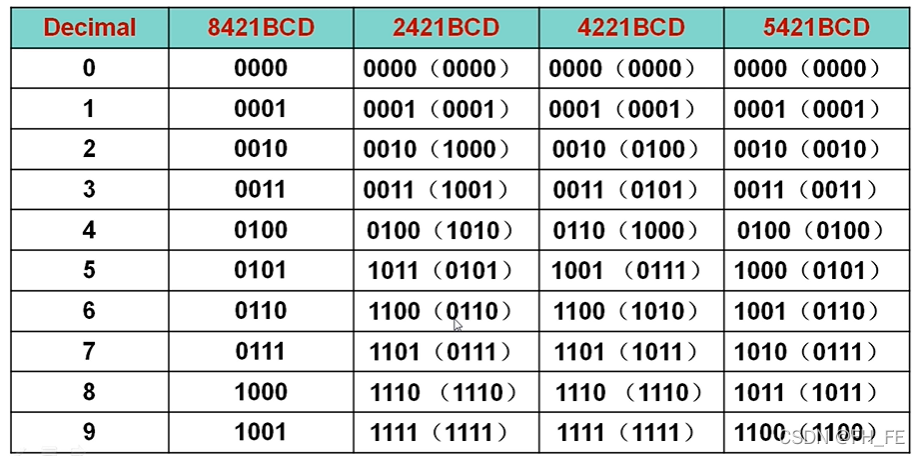
    在这里插入图片描述

    在这里插入图片描述
    除 8421BCD 其余编码不唯一，分为A码和B码
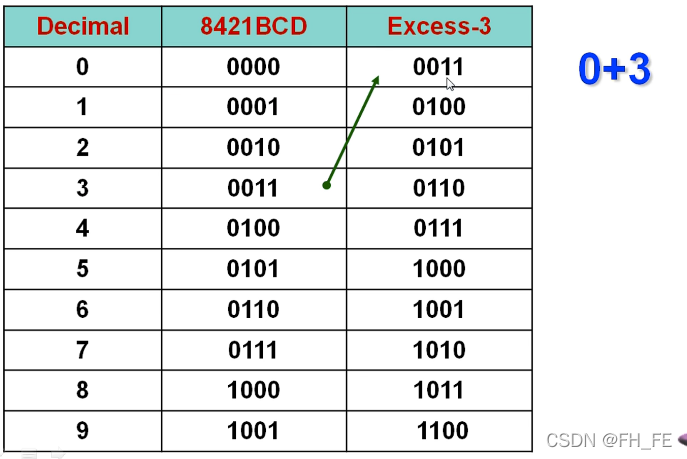
    而且对于 2421BCD 和 4221BCD具有自补码的特点 0-9编码互补， 1-8互补 。。。

    2.2 余3码

    在 8421BCD码的基础上 +3
    是自补码
    无权码
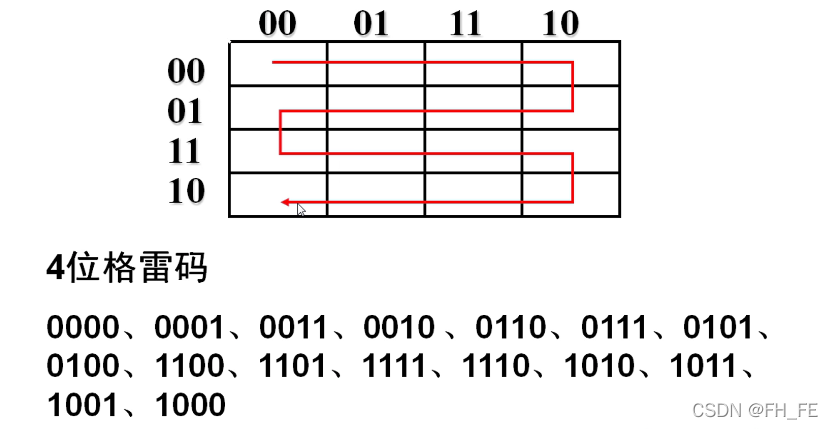
    在这里插入图片描述

    2.3 典型格雷码（Gray code）

    无权码
    相邻两数之间只有一位码元不同
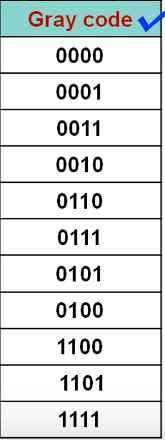
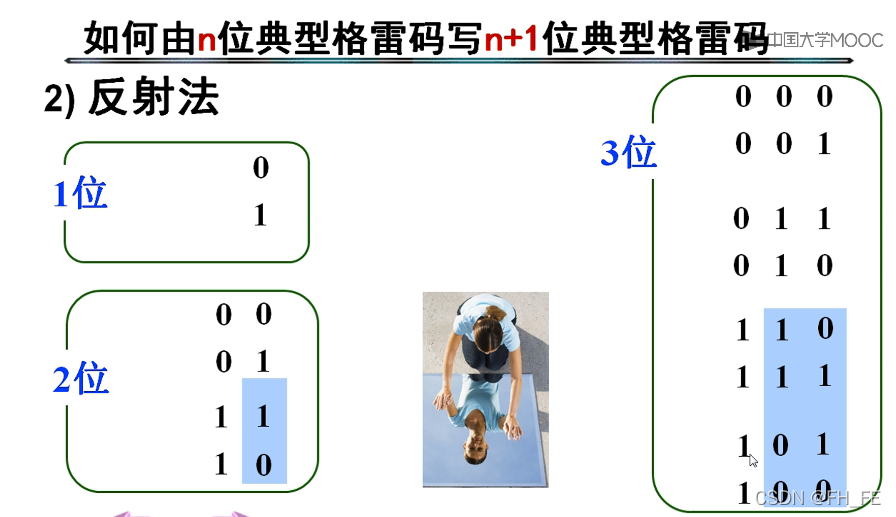
    在这里插入图片描述

    如何写出Gray code
    先取二进制数，保留有效的最高位，然后从最高位开始，依次比较相邻的二进制数，相同0，不同1
    在这里插入图片描述

    向下做镜面对称，然后在左边补位，上一半为0，下一半为1
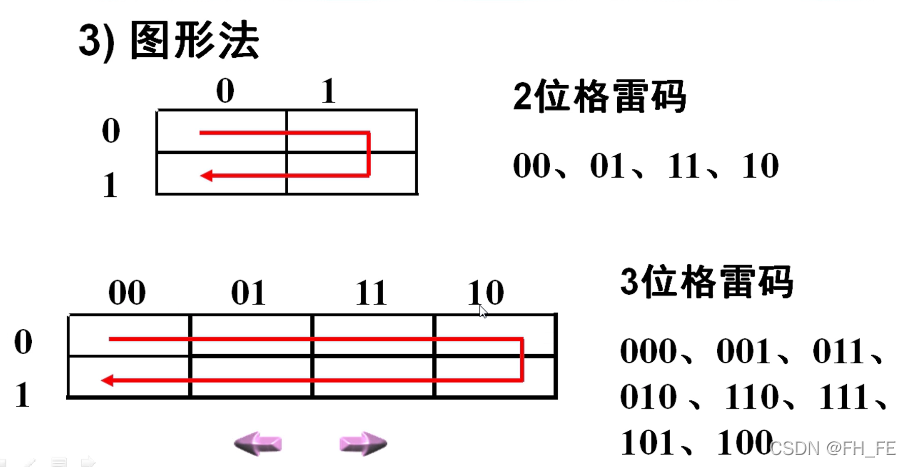
    在这里插入图片描述

    顺时针读取
    每个格的格雷码为 左上
    偶数：左与上等长
    奇数：左短右长
    在这里插入图片描述
    在这里插入图片描述

    gray code应用
    传输数据时，数据的改变数越少，越不容易犯错
    当数值连续变化时，使用gray code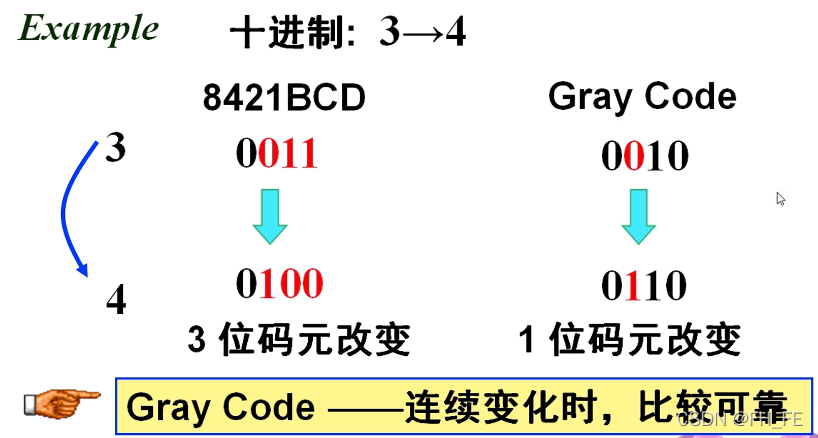

    在这里插入图片描述

    3. 基本逻辑运算

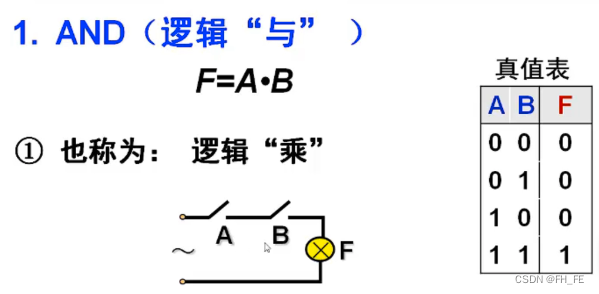
    3.1 AND（“与”运算）

    A,B同时打开
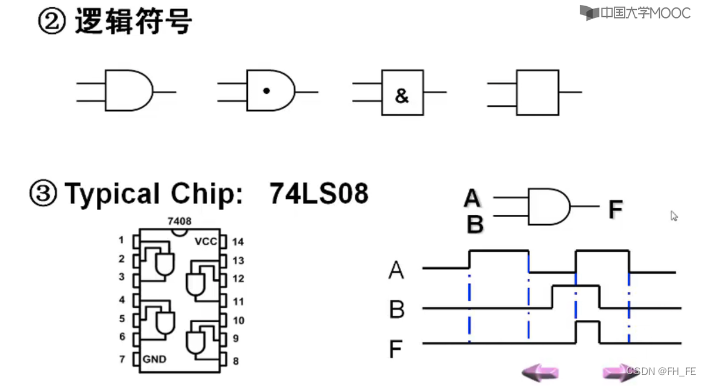
    在这里插入图片描述

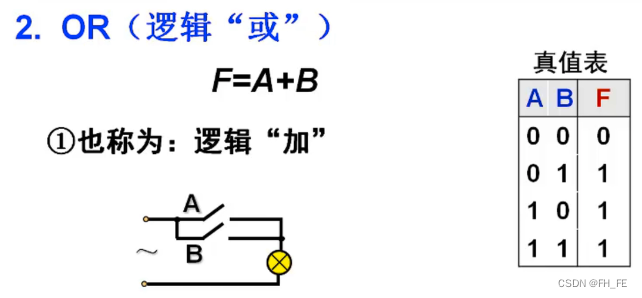
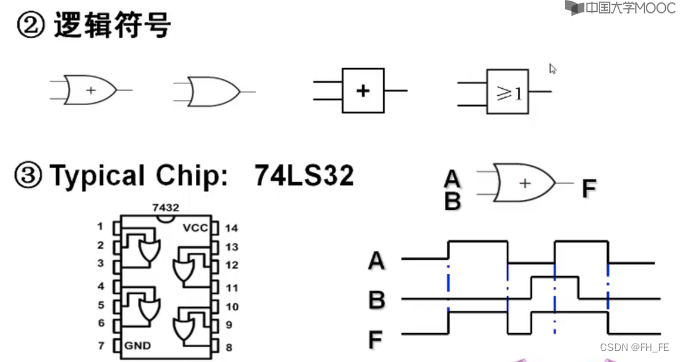
    在这里插入图片描述

    3.2 OR)

    在这里插入图片描述

    3.3 NOT

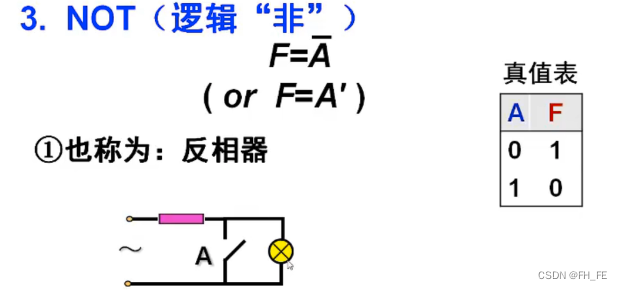
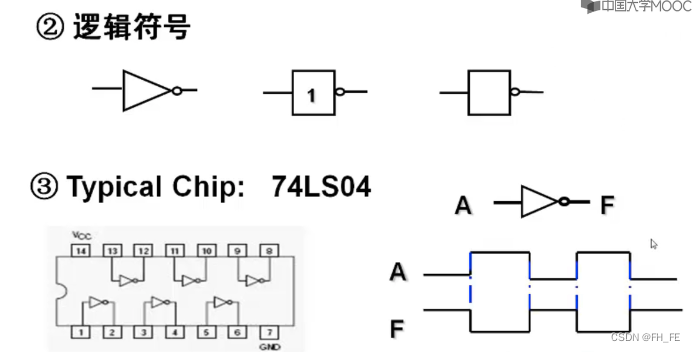
    在这里插入图片描述

    在这里插入图片描述

    4. 符合逻辑运算

    4.1 与非（NAND）

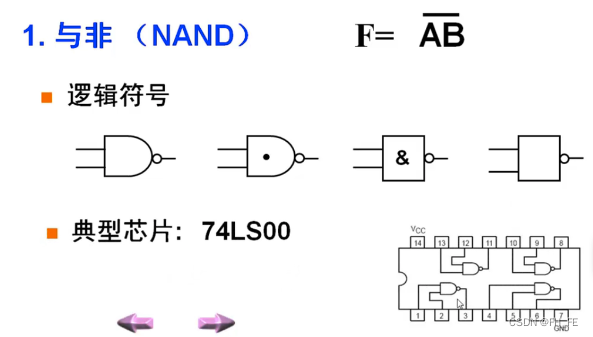
    在这里插入图片描述

    4.2 或非（NOR）

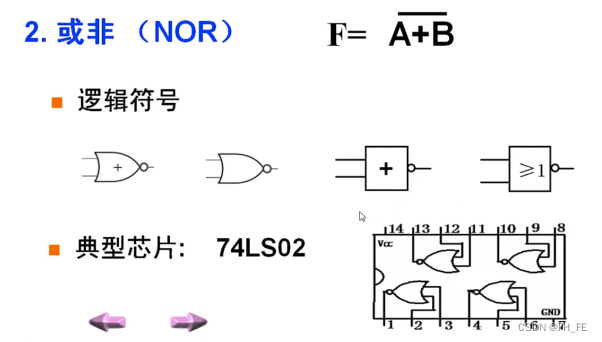
    在这里插入图片描述

    4.3 与或非（AND-OR-NOT）

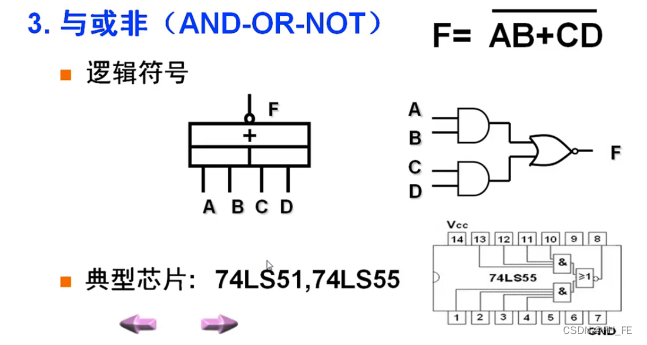
    在这里插入图片描述

    4.4 异或

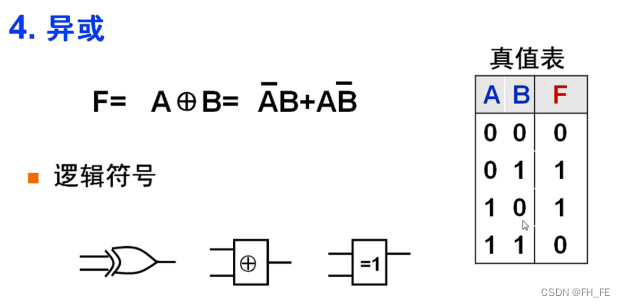
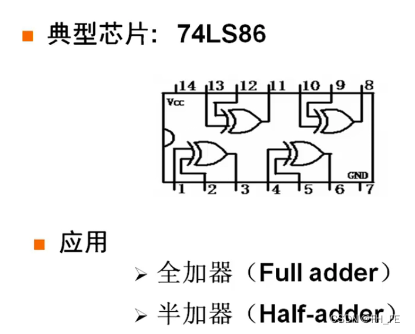
    在这里插入图片描述
    在这里插入图片描述
    半加器
    异或得到同位数的结果
    与门得到进位的结果
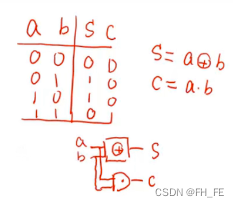
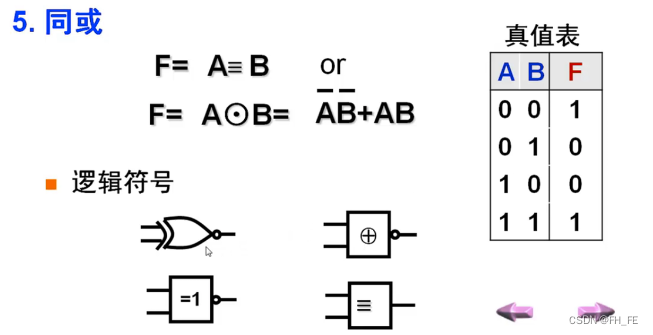
    在这里插入图片描述

    4.5 同或

    异或门的非

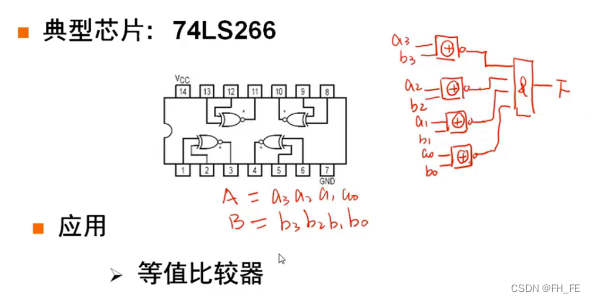
    在这里插入图片描述
    在这里插入图片描述
    等值比较器实现：
    例如比较四位的两个数A、B，相同位输入一个同或门（同为1，异为0），再将同或门的输出输入与门，输出结果F为0，则A、B不相等，F为1则A、B相等。

    4.6 异或及同或运算的性质

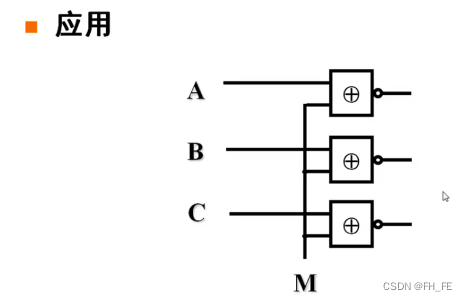
    在这里插入图片描述
    在这里插入图片描述
    由异或非（同或）的性质可知

    5. 逻辑函数的表示方法

    有四种表示方法，可以相互转化
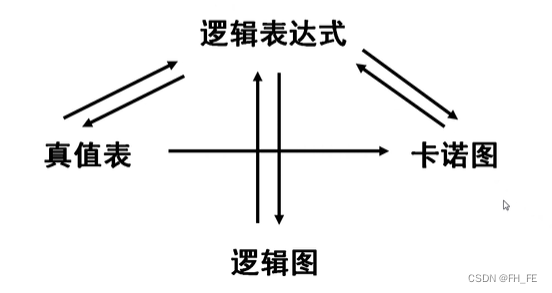
    在这里插入图片描述

    5.1 逻辑表达式 -> 逻辑图

    逻辑表达式，用门电路表示为逻辑图
    电路分析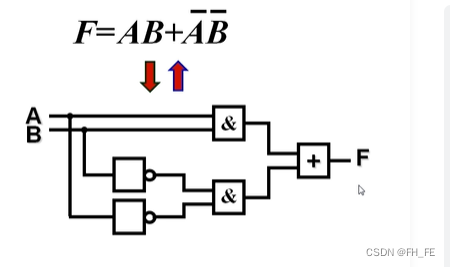

    在这里插入图片描述

    5.2 真值表转化为逻辑表达式

    如果两个逻辑函数的真值表相同，则这两个逻辑函数是相等的。

    从真值表转化为逻辑表达式
    标准与或式
    选择逻辑结果为1的项与到一起即可
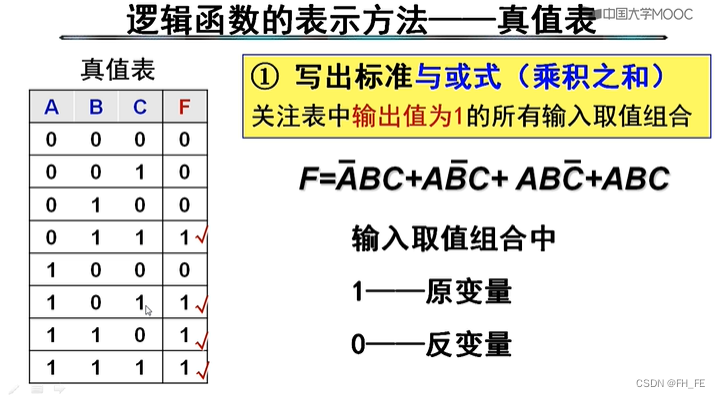
    在这里插入图片描述
    标准或与式

    找逻辑结果为0的项，先或再与
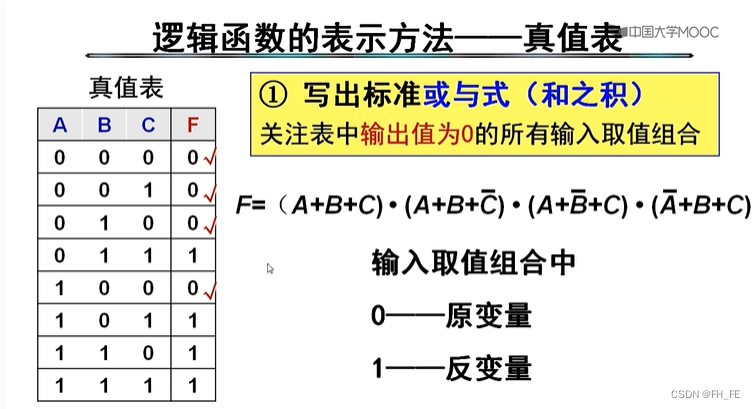
    在这里插入图片描述

    6. 逻辑代数定理和规则

    6.1 公理

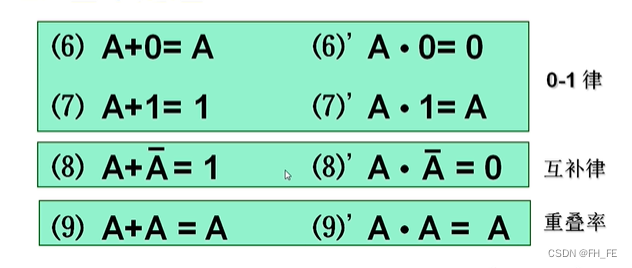
    在这里插入图片描述

    6.2 基本定理

    在这里插入图片描述
    在这里插入图片描述
    零一率和重叠率的应用
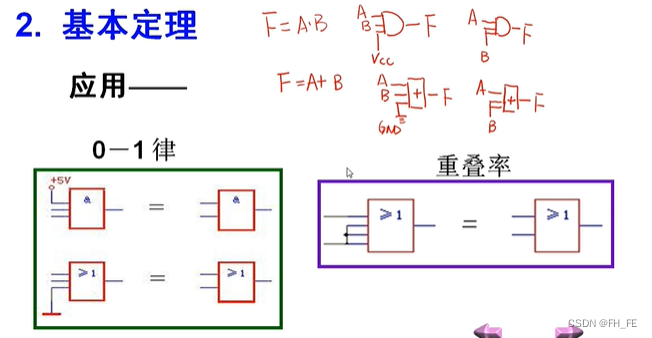
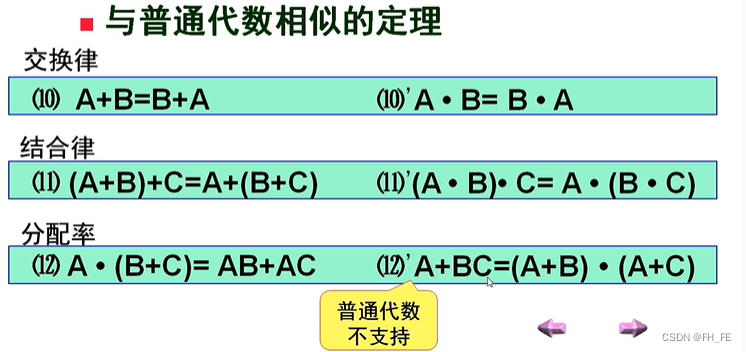
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    上标D表示对偶，互为对偶的两个表达式不一定相等，只有当两个逻辑表达式本来就相等时，其对偶相等
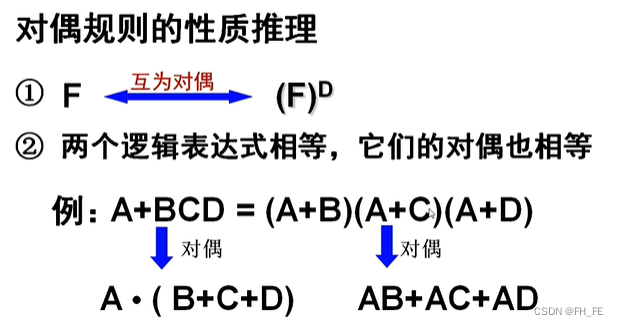
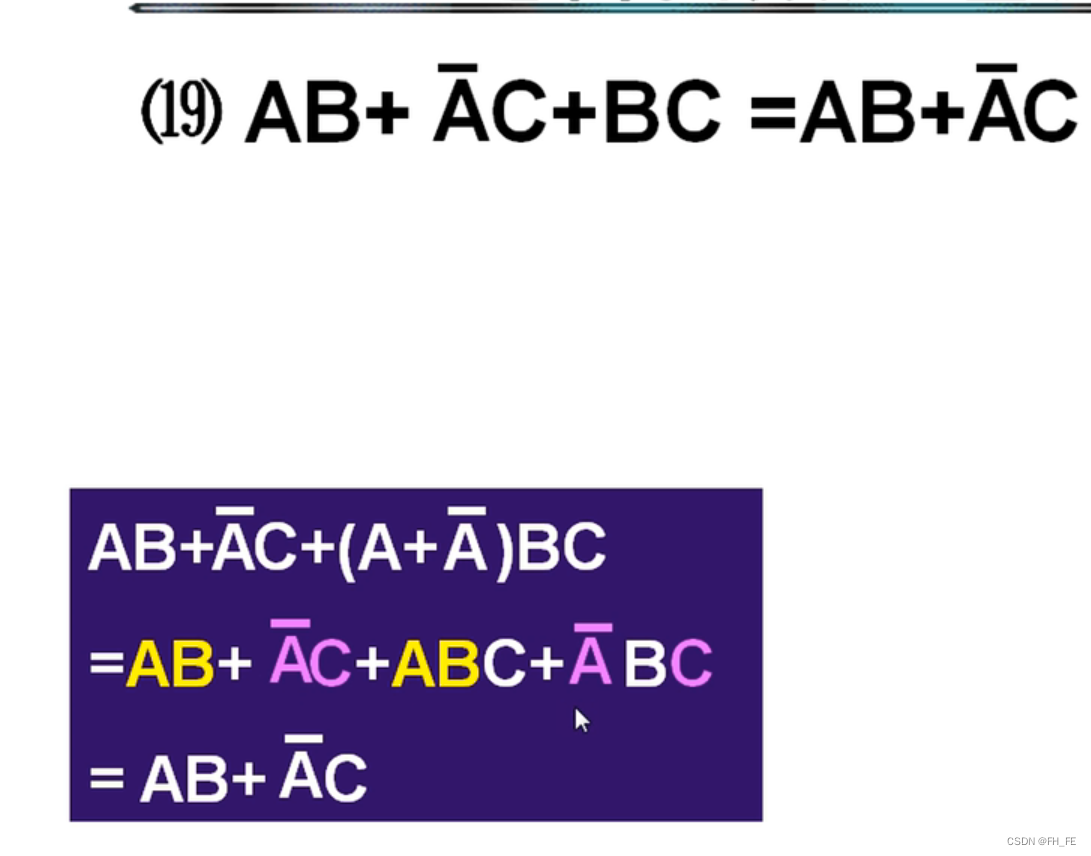
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    由于公式（19）成立，等式两边分别取对偶，得到等式 ( 19 ) ’’ (19)^{ ’’} (19)’’成立
    ( A + B ) ( A + A ‾ + B + C ) ( A ‾ + C ) (A + B)(A + \overline{A} + B + C)(\overline{A} + C) (A+B)(A+A+B+C)(A+C)

    7. 代数化简法

    在这里插入图片描述
    在这里插入图片描述
    为什么要化简逻辑表达式？

    1. 逻辑门的数量少，用的芯片个数少，成本低
    2. 逻辑门的输入个数少，更稳定
      在这里插入图片描述
      例题
      在这里插入图片描述
      在这里插入图片描述
      函数逻辑表达式和其对偶式是不一样的，需要取两次对偶才能和原表达式相等
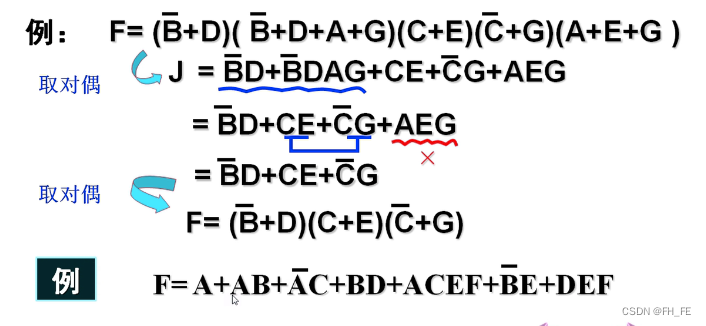
      在这里插入图片描述
      解：
      F = A + A ‾ C + B D + B ‾ E + D E F F=A + \overline{A}C + BD + \overline{B}E + DEF F=A+AC+BD+BE+DEF
      F = A + A ‾ C + B D + B ‾ E F=A + \overline{A}C +BD + \overline{B}E F=A+AC+BD+BE 消除冗余项
      F = ( A + A ‾ ) ( A + C ) + B D + B ‾ E F=(A + \overline{A})(A + C) + BD + \overline{B}E F=(A+A)(A+C)+BD+BE
      F = A + C + B D + B ‾ E F=A + C + BD + \overline{B}E F=A+C+BD+BE

    8. 最大项和最小项表达式

    最小项表达式：所有项都是1的标准与或式
    在这里插入图片描述
    最大项表达式：最大项乘积
    所有输出值为0的取值组合
    在这里插入图片描述

    最大项和最小项的性质

    最小项性质

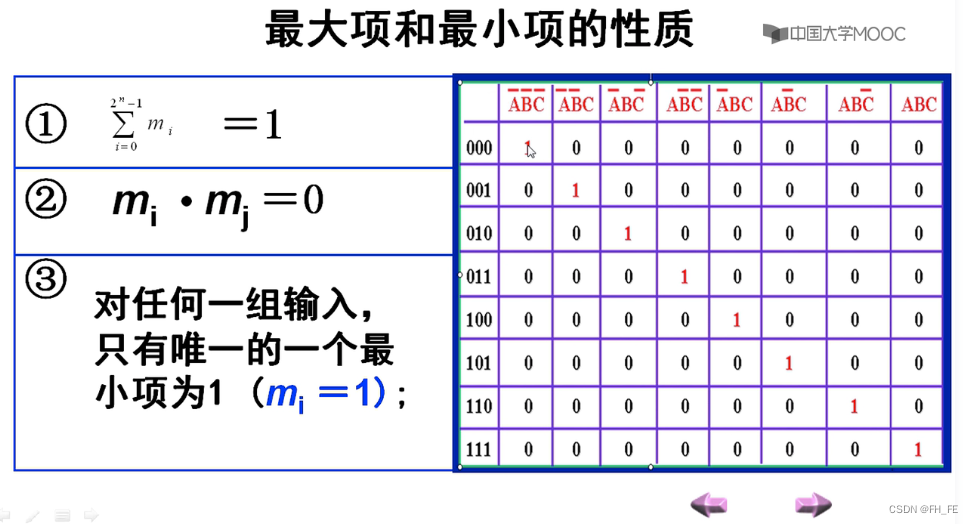
    在这里插入图片描述

    最大项性质

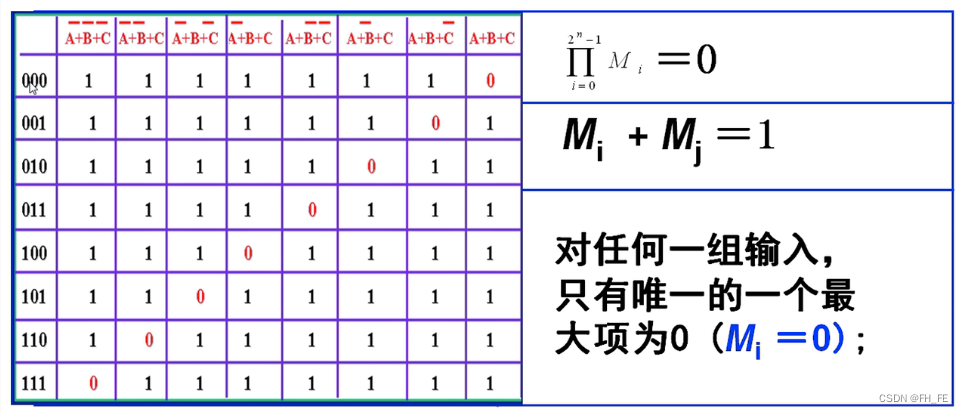
    在这里插入图片描述

    原函数整体取反得到反函数
    取对偶的到对偶函数:原函数和对偶函数之间是互补的（即相加等于7）
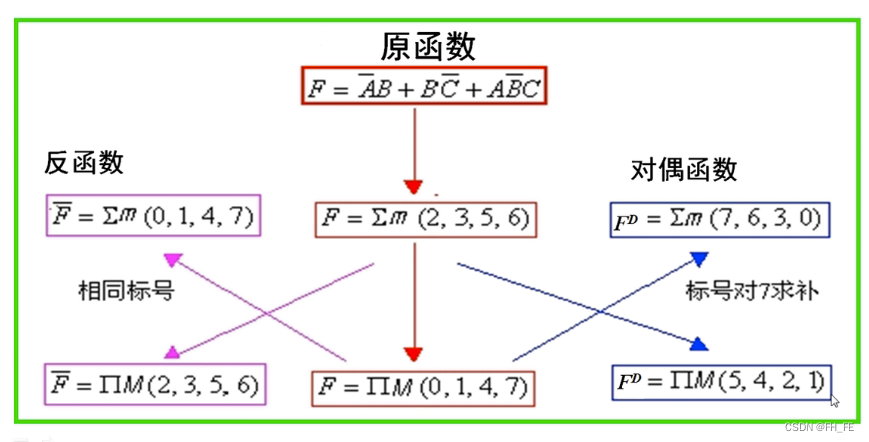
    在这里插入图片描述
    F = A ‾ B + B C ‾ + A B ‾ C F=\overline{A}B + B\overline{C} + A\overline{B}C F=AB+BC+ABC
    A ‾ B : \overline{A}B: AB: 010 或 011
    B C ‾ : B\overline{C}: BC: 010 或 110
    A B ‾ C : A\overline{B}C: ABC: 101
    F = ∑ m ( 2 , 3 , 5 , 6 ) F=\sum{m(2, 3, 5, 6)} F=∑m(2,3,5,6)

    9. 不完全给定函数

    9.1 无关项

    无关项：

    1. 不可能存在的输入组合
    2. 所有输入都存在，但是对于某些输出我们并不关心（8421BCD码转化成余三码的过程中，8421BCD码取值范围是0~9，所以大于1001的部分没有意义）

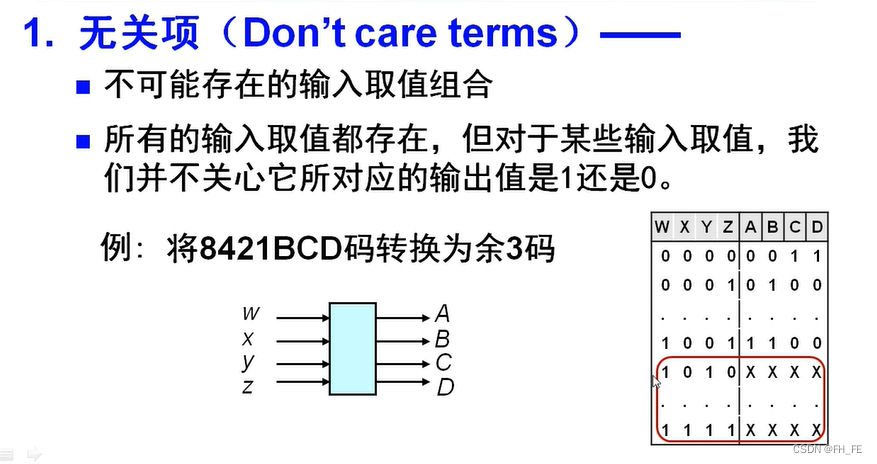
    在这里插入图片描述

    9.2 不完全给定函数

    带有无关项的函数
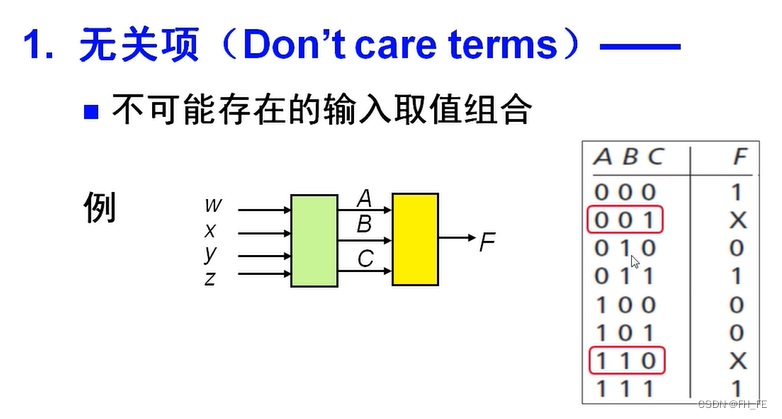
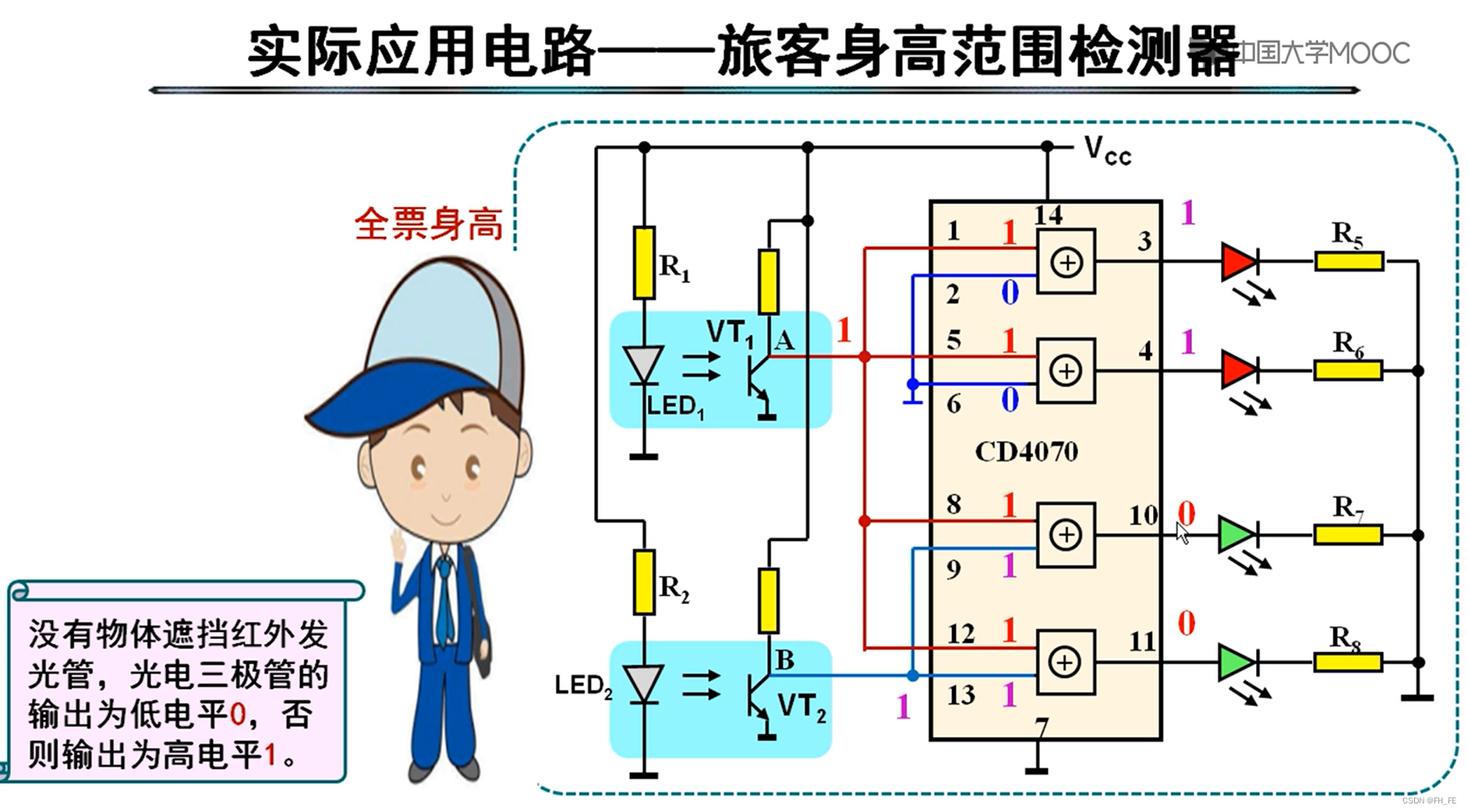
    在这里插入图片描述

    在这里插入图片描述

    9.3 实际应用电路

    测试全票、半票的带光电检测电路
    用了红外发光管LED和光电三极管，红外被遮挡时三极管被拉高
    中间有一个有四个异或门构成的CMOS

    半票绿灯亮起，全票红灯亮起，免票不亮（矮矮的小可爱）
    在这里插入图片描述
    在这里插入图片描述

  • 相关阅读:
    Vitis_米联客开发板MZU07_7EG上手_1
    文件列表创建工具 Nifty File Lists mac中文版功能特色
    创建maven的 java web项目
    数学小抄: 概率角度推导Kalman Filter
    Python 3.11 版本是对线程安全做了什么更改吗
    AI时代中小企业算力需求爆发，惠普发布新品战99 Monster满血高算工作站
    【架构师视角系列】Apollo配置中心之Server端（ConfigSevice）（三）
    Kubernetes-三大开放接口-初见
    【c】指针
    【微信小程序】实现投票功能（附源码）
  • 原文地址：https://blog.csdn.net/zhiai_/article/details/123680467