博弈论与SG函数入门

博弈论概述

• Nim Game —— 尼姆博弈
• Bash Game —— 巴什博弈
• Wythoff’s Game —— 威佐夫博弈
• Anti Nim —— 反Nim游戏

(游戏都建立在双方都有最优策略的情况下，若未加以说明，则每人每次至少取一个石子)

Nim游戏

历史渊源

给出n列珍珠，两人轮流取珍珠，每次在某一列中取至少1颗珍珠，但不能在两列中取。最后拿光珍珠的人输。这种游戏称为"拈(nian，谐音为Nim)"。据说它源自中国，经由被贩卖到美洲的奴工们外传。辛苦的工人们在工作闲暇之余，用石子玩游戏以排遣寂寞。后来流传到高级人士，则用便士(Pennies)在酒吧柜台上玩。最有名的玩法，是把十二枚便士放成3、4、5三列，拿光铜板的人赢。后来，大家发现，先取的人只要在3那列里取走2枚，变成了1、4、5，就能稳操胜券了，游戏也就变得无趣了。于是大家就增加列数，增加铜板的数量，这样就让人们有了毫无规律的感觉，不易于把握。直到本世纪初，哈佛大学数学系副教授查理士•理昂纳德•包顿(Chales Leonard Bouton)提出一篇极详尽的分析和证明，利用数的二进制表示法，解答了这个游戏的一般法则。

Nim游戏例题

那么，到底什么是Nim游戏呢？下面以一道例题引入Nim游戏。
你和你的朋友，两个人一起玩Nim游戏，游戏规则如下：
桌子上有一堆石子，你们轮流进行自己的回合， 你作为先手 。每一回合，轮到的人拿掉1~3颗石子。拿掉最后一颗石子的人就是获胜者。假设你们每一步都是最优解。请编写一个函数，来判断你是否可以在给定石子数量为n的情况下赢得游戏。如果可以赢，返回true；否则，返回false 。Nim游戏原题链接

Nim游戏题目大意

有两个游戏者A和B，有n颗石子。约定：两人轮流取走石子，每次可取1、2或3颗。A先取，取走最后一颗石子的人获胜。问胜负情况。

Nim游戏胜负情况分析

当n = 0的时候，B获胜
如果n为0，A取石子的时候已经没有了石子，等价于最后一颗石子被B取走，即B获胜。

当n = 1的时候，A获胜
A直接取走第一颗石子，则A获胜

当n = 2的时候，A获胜
A直接取走前两颗石子，则A获胜

当n = 3的时候，A获胜
A直接取走前三颗石子，则A获胜

当n = 4的时候，B获胜
此时，一定是B胜。为什么？以下是可能的结果:

• A移除1颗石子。B移走了3颗石子，包括最后一颗，所以是B赢。
• A移除2颗石子。B移走2颗石子，包括最后一颗，所以还是B赢。
• A移走3颗石子。B移走最后一颗石子。仍然是B赢。
• 在所有结果中，B都是赢家。

结论：当有4颗石子时，谁先取石子，谁就输

当n = 5的时候，A获胜
前面提到，双方都有最优策略。如果A在第一步只取一颗石子，那么还剩四颗石子，这四颗石子由B先取，所以B一定输。

当n = 6的时候，A获胜
同理，如果A在第一步只取两颗石子，那么还剩四颗石子，这四颗石子由B先取，所以B一定输。

当n = 7的时候，A获胜
同理，如果A在第一步只取三颗石子，那么还剩四颗石子，这四颗石子由B先取，所以B一定输。

当n = 8的时候，B获胜
A先取，A可能先取1，2，3颗石子

• A取一颗，还剩七颗，由B来取。由以上分析知，当n为7时，谁先取，谁获胜，所以B获胜。
• A取两颗，还剩六颗，由B来取。由以上分析知，当n为6时，谁先取，谁获胜，所以B获胜。
• A取三颗，还剩五颗，由B来取。由以上分析知，当n为5时，谁先取，谁获胜，所以B获胜。

结论：当有8颗石子时，谁先取石子，谁就输

Nim游戏结论总结

• 当n为4的倍数时，谁先取，谁就输（当n为0，4，8，12……时，A先取，必定会输。）
• 当n为非4的倍数时，谁先取，谁就赢（当n不为0，4，8，12……时，A只需要将n取成4的倍数，这样就变成了B先取，B一定会输。）
• 即如果n % 4为0，则为先手必败状态。反之，则为先手必胜状态。

//LeetCode 292. Nim 游戏 ac代码
class Solution {
public:
    bool canWinNim(int n) {
        if (n % 4 == 0) return false;
        else return true;
    }
};
1
2
3
4
5
6
7
8

Bash博弈

我们推广一下，每次不一定取1、2、3颗，而是取1~m颗：那么我们就可以得到：如果 n % ( m + 1 ) = 0 ，即为先手必败状态，否则为先手必胜状态。即巴什博弈（Bash Game）

Bash博弈题目大意

有两个游戏者A和B，有n颗石子。约定：两人轮流取走石子，每次可取1、2、3或4颗。A先取，取走最后一颗石子的人获胜。问胜负情况。(m = 4)

Bash博弈胜负情况分析

当n = 0的时候，B获胜
如果n为0，A取石子的时候已经没有了石子，等价于最后一颗石子被B取走，即B获胜。

当n = 1的时候，A获胜
A直接取走第一颗石子，则A获胜

当n = 2的时候，A获胜
A直接取走前两颗石子，则A获胜

当n = 3的时候，A获胜
A直接取走前三颗石子，则A获胜

当n = 4的时候，A获胜
A直接取走前四颗石子，则A获胜

当n = 5的时候，B获胜

• A取走第一颗石子，还剩四颗石子。这四颗石子B可以全部取走，所以B获胜。
• A取走前两颗石子，还剩三颗石子。这三颗石子B可以全部取走，所以B获胜。
• A取走前三颗石子，还剩两颗石子。这两颗石子B可以全部取走，所以B获胜。
• A取走前四颗石子，还剩一颗石子。最后一颗石子被B取走，所以B获胜。
• 综上，B一定可以获胜。此时，n % (m + 1) = 5 % (4 + 1) = 0
• 以此类推，与Nim博弈一样，可以得到当n % ( m + 1 ) = 0时为先手必败状态，否则为先手必胜状态。

Nim游戏和Bash游戏的特点

• 两人游戏。
• 两人轮流走步。
• 有一个状态集，而且通常是有限的。(在Nim博弈和Bash博弈中，石子得个数为n，就是一个n个大小的状态集合)
• 有一个终止状态，到达终止状态后游戏结束。
• 游戏可以在有限的步数内结束。
• 规定好了哪些状态转移是合法的。(在Nim博弈和Bash博弈中，每次可以取不超过m个石子就是合法的状态)
• 所有规定对于两人是一样的
• 事实上，Nim游戏和Bash游戏都是平等组合游戏(ICG)
• 那么，什么是平等组合游戏(ICG)呢?

关于博弈论的一些名词解释

Impartial Combinatorial Games / ICG

• Nim游戏是组合游戏 (Combinatorial Games) 的一种，准确来说，属于"Impartial Combinatorial Games"（以下简称 ICG）。
• 满足以下条件的游戏是ICG：
  1、有两名选手
  2、两名选手交替对游戏进行移动(move)，每次一步，选手可以在有限的合法移动集合中任选一种进行移动
  3、对于游戏的任何一种可能的局面，合法的移动集合只取决于这个局面本身，不取决于轮到哪名选手操作、以前的任何操作、骰子的点数或者其它什么因素；
  4、如果轮到某名选手移动，且这个局面的合法的移动集合为空(也就是说此时无法进行移动)，则这名选手负。
  5、根据这个定义，很多日常的游戏并非ICG。例如象棋就不满足条件3，因为红方只能移动红子，黑方只能移动黑子，合法的移动集合取决于轮到哪名选手操作

N-position / P-position

• 首先需要注意：此处的先手，指的并不是整个游戏一开始，先取石子的那方。而是在当前局面，要进行操作的叫先手。
• N-position：又叫先手必胜状态。
• P-position：又叫先手必败状态。解释：当前石子个数为0时，如果轮到A取石子，说明B取走了最后一个石子，B获胜，A失败，即先手必败。同理，如果轮到B取石子，说明A取走了最后一个石子，A获胜，B失败，还是先手必败。也就是说，n为0是先手必败状态。
• 如LeetCode 292. Nim 游戏，0，4，8，12……等状态就是对于先手的P-position（必败状态），其他的则是对于先手的N-position（必胜状态）。
• 那么我们定义两个状态之间的转换：
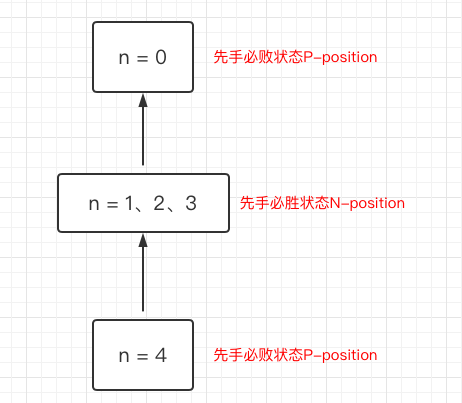
• 无法进行任何移动的局面（也就是terminal position）是P-position。解释：n为0时，无法进行任何移动，所以其为先手必败状态。
• 可以移动到P-position的局面是N-position。解释：在Nim游戏中，当n = 1、2、3时，此时如果是A来取(A是先手)，A可以取走全部石子，A获胜。此时A使得n从1、2、3变为0，即到了先手必败状态，所以可以移动到P-position的局面是N-position。
• 所有移动都导致N-position的局面是P-position。根据下图，由上一条分析，已知在Nim游戏中，n为1、2、3时，是先手必胜状态，而当n为4时，不管面临此局面的先手是取走1颗石子(剩3)，还是2(剩2)或3(剩1)颗石子，都将导致N-position，所以n=4是先手必败局面P-position。
  

异或运算Xor(^)

为什么先介绍异或运算？在证明Nim游戏的正确性时需要用到

异或运算的法则：

• 如果a、b两个值不相同，则异或结果为1
• 如果a、b两个值相同，异或结果为0
• 举例：根据下面的真值表，1 ^ 4 = (0001) ^ (0100) = (0101) = 5
• 相同为0，不同为1。记忆方法：男男不能生，女女不能生，男女可以生，女男可以生

异或运算的性质

• 异或的异或是自己。举例：a ^ b ^ b = a
• 消去率：如果a ^ c = b ^ c，则可以推出 a = b

Nim游戏的结论

20世纪初，哈佛大学Charles Leonard Bouton教授提出通常的Nim游戏的定义是这样的：有若干堆石子，每堆石子的数量都是有限的，合法的移动是"选择一堆石子并拿走若干颗(不能不拿)"，如果轮到某个人时所有的石子堆都已经被拿空了，则判负（因为他此刻没有任何合法的移动）

设这N堆石子的数量分别为a1，a2， …，an。对于Nim游戏，当且仅当所有堆石子的数量都异或起来结果为0时，局面是必败态。即：当且仅当a1 ^ a2 ^ … ^ an = 0时，先手必败。

证明：Nim游戏的结论

• 无法进行任何移动的局面是必败态：
  当a1 = a2 = a3 = … = an = 0时，必有a1 ^ a2 ^ … ^ an = 0。也就是说，任意多个0做异或运算，结果仍然是0。
• 可以移动到必败态的局面是非必败态(非必败态可以移动到必败态)
  假设在某一局面这N堆石子的数量分别为a1，a2， …，an，如果a1 ^ a2 ^ … ^ ai ^ … ^ an = k≠0，则一定存在一个ai’，使得a1 ^ a2 ^ … ^ ai’ ^ … ^ an = 0，其中，ai’ = ai ^ k。
• 在必败态做的所有操作的结果都是非必败态(必败态只能移动到非必败态)
  如果在当前局面，保证了a1 ^ a2 ^ … ^ ai ^ … ^ an = 0，那么，一定不存在一个合法的移动，将ai变为ai’之后，可以使得a1 ^ a2 ^ … ^ ai’ ^ … ^ an = 0。为什么呢？
  因为：
  a1 ^ a2 ^ … ^ ai-1 ^ ai ^ ai+1 ^ … ^ an
  = a1 ^ a2 ^ … ^ ai-1 ^ ai+1 ^ … ^ an ^ ai(将ai提到最后)
  = 0
  设a1 ^ a2 ^ … ^ ai-1 ^ ai+1 ^ … ^ an = k
  则有k ^ ai = 0；—— ①
  将将ai变为ai’之后，
  如果k ^ ai’ = 0；—— ②
  由①②两式，得k ^ ai =k ^ ai’ ，进而得到ai = ai’，与ai不等于ai’矛盾。证明完毕。

根据以上分析以及下图，假设A为先手，且处于必胜态的位置，先通过第①步，选择转化为必败态，必败态通过第②步，又只能转化为必胜态…最终可以得到A胜出

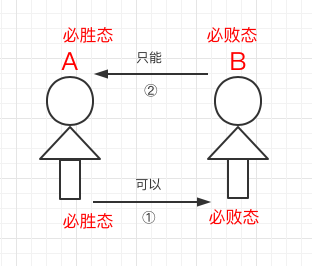
要证Nim游戏的正确性，只要证明当且仅当a1 ^ a2 ^ … ^ an = 0时，满足以上三个条件即可。

SG函数 ( Sprague - Garundy )

SG函数的引入

如果把Nim的规则略加改变，比如说：有n堆石子，每次可以从第1堆石子里取1颗、2颗或3颗石子，可以从第2堆石子里取奇数颗石子，可以从第3堆及以后的石子里取任意颗……在这种规则下，如何寻找必胜态？这种时候，就需要引入SG函数来解决问题。

有向无环图 DAG的引入

什么是有向无环图？顾名思义，它满足：

• 有方向
• 无环路

如下图：

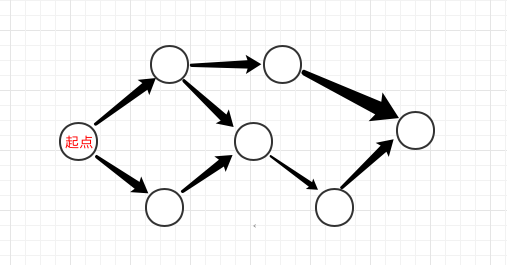
给定一个有向无环图和一个起始顶点上的一枚棋子，两名选手交替的将这枚棋子
沿有向边进行移动，无法移动者判负。事实上，这个游戏可以认为是所有
Impartial Combinatorial Games的抽象模型。也就是说，任何一个ICG都可以通过
把每个局面看成一个顶点，对每个局面和它的子局面连一条有向边来抽象成这个
“有向图游戏”。下面我们就在有向无环图的顶点上定义Sprague-Garundy函数

mex运算引入

首先定义mex (minimal excludant)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如mex{0, 1, 2, 4} =3、mex{0, 1, 2, 5} =3、mex{2, 3, 5} =0、mex{} =0。
对于一个给定的有向无环图，定义关于图的每个顶点的Sprague-Garundy函数g如下：g (x) = mex { g (y) | y是x的后继 } 。

SG函数的性质(了解)

• 所有的最终位置terminal position所对应的顶点，也就是没有出边的顶点，其
  SG值为0。
• 对于一个g(x) = 0的顶点x，它的所有后继y都满足g(y) != 0。
• 对于一个g(x) != 0的顶点，必定存在一个后继节点满足g(y) = 0。

结论

当且仅当g(x) = 0时，顶点x所代表的position是P-position。(不做证明)
即：我们通过计算有向无环图的每个顶点的SG值，就可以对每种局面找到必胜策略。但SG函数的用途远没有这样简单。如果将有向图游戏变复杂一点，比如说，有向图上并不是只有一枚棋子，而是有n枚棋子，每次可以任选一颗进行移动，这时怎样找到必胜策略呢？