【Reinforcement Learning】策略学习

强化学习最主要的两种方式之一，策略学习的究竟是怎么回事？此处笔记根据B站课程，王树森老师的强化学习记录而来。3.深度强化学习(3_5)：策略学习 Policy-Based Reinfor(Av374239425,P3)_哔哩哔哩_bilibili

Policy-based Reinforcement Learning 策略学习

1.回顾策略函数

策略学习的本质就是使用一种方式来近似策略函数Π(a|s), Policy Function Approximation

Policy Function Π(a|s) ,其是一个概率密度分布PDF,使用网络来近似策略函数，则输入是state s,输出是该条件下各个动作的概率，根据概率进行随机抽样，选择下一个action。在这个过程中，Π(a|s)控制agent做出反应。

想要让agent玩超级玛丽这样的游戏，并不能把所有的状态和动作记录下来，所以我们要做函数近似，学习一个函数近似策略函数，近似的方法是多种多样的。

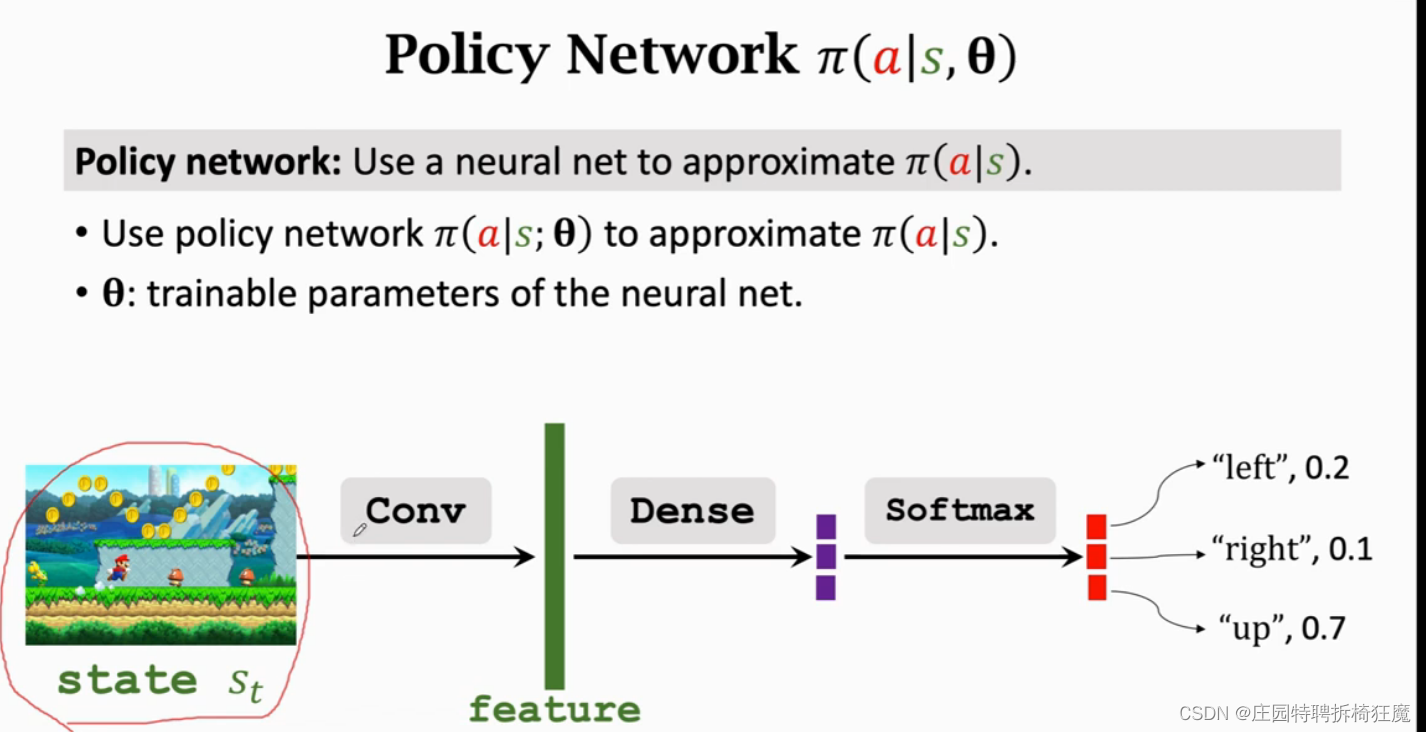
 策略网络，Policy Network,使用一个神经网络近似Π(a|s)

Model   Π(a|s;θ) ————近似——>Π(a|s),其中θ是要学习的参数。

由于Π是概率密度函数PDF，所以有性质：

 已知动作价值函数QΠ，在其基础上，去除策略Π的影响，得到状态价值函数VΠ，可以评价当前状态的好坏，也能评价策略policy Π的好坏，VΠ越大，说明policy Π越好。

 2.Policy-base Reinforcement Learning策略基础的强化学习

使用神经网络来代替策略函数Π，该神经网络就叫做策略网络。

 

为了使V(s;θ) 足够大，我们调整θ的值，其中V(S;θ)对S求期望，则J(θ)就只与θ的值相关。当观测到状态s时，使用策略梯度更新θ的值。这里使用的是梯度上升，实际就是随机梯度，随机性来自s,目标是让J(θ)越来越大。

这里的梯度并不是真正的梯度，真正的梯度是目标函数（价值）关于θ的导数，这里只是VΠ(状态转移函数)关于θ的导数。

3.策略梯度如何计算？Policy Gradient

V(s,θ)是对state-value function的近似，梯度是V对θ的导数，推到过程大致如下：

这里做一个假设，QΠ不依赖于θ，这个假设是为了简单理解，并不严谨，因为QΠ是依赖于θ的。

在此处得到了策略梯度计算的第一个公式，但实际应用中并不这么用，都是使用蒙特卡洛近似。因为Π在这里是复杂的神经网路，并不能简单的计算积分。

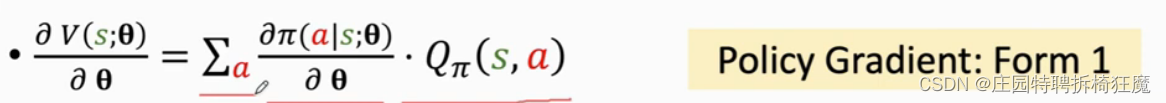 接下来做蒙特卡洛近似：从上往下推不太好推，但是可以从下往上验证：使用链式法则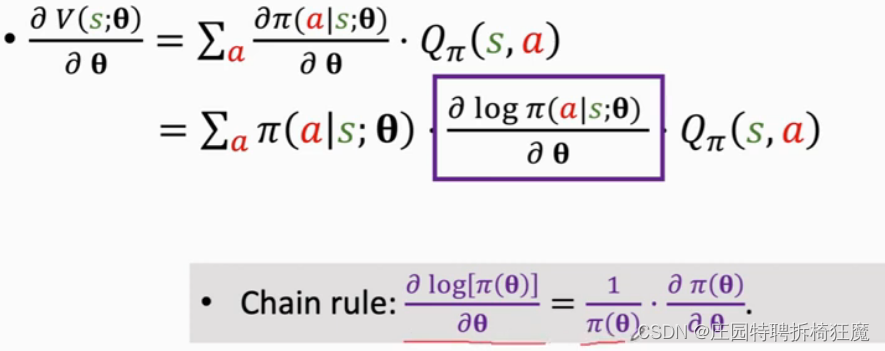

 

 

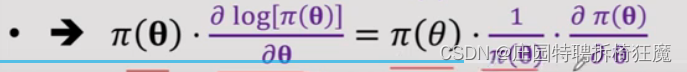
因此得到策略梯度的两种等价形式：

 

3.计算策略梯度函数：离散、连续

 

 

 4.算法：

 如何计算qt,有两种方式：第一种方式用u(t)替代QΠ函数，需要玩完一局游戏，观测到所有奖励，才能更新网络。另一种方式是使用神经网络近似QΠ，这样就有两个神经网络，一个近似Π，一个近似QΠ，叫做actor-critic模型。

 

Summary