图解LeetCode——998. 最大二叉树 II（难度：中等）

一、题目

最大树 定义：一棵树，并满足：其中每个节点的值都大于其子树中的任何其他值。

给你最大树的根节点 root 和一个整数 val 。

就像 之前的问题（654. 最大二叉树） 那样，给定的树是利用 Construct(a) 例程从列表 a（root = Construct(a)）递归地构建的：

• 如果 a 为空，返回 null 。
• 否则，令 a[i] 作为 a 的最大元素。创建一个值为 a[i] 的根节点 root 。
• root 的左子树将被构建为 Construct([a[0], a[1], ..., a[i - 1]]) 。
• root 的右子树将被构建为 Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]]) 。
• 返回 root 。

请注意，题目没有直接给出 a ，只是给出一个根节点 root = Construct(a) 。

假设 b 是 a 的副本，并在末尾附加值 val。题目数据保证 b 中的值互不相同。返回 Construct(b) 。

二、示例

2.1> 示例 1：

【输入】root = [4,1,3,null,null,2], val = 5
【输出】[5,4,null,1,3,null,null,2]
【解释】a = [1,4,2,3], b = [1,4,2,3,5]

2.2> 示例 2：

【输入】root = [5,2,4,null,1], val = 3
【输出】[5,2,4,null,1,null,3]
【解释】a = [2,1,5,4], b = [2,1,5,4,3]

2.3> 示例 3：

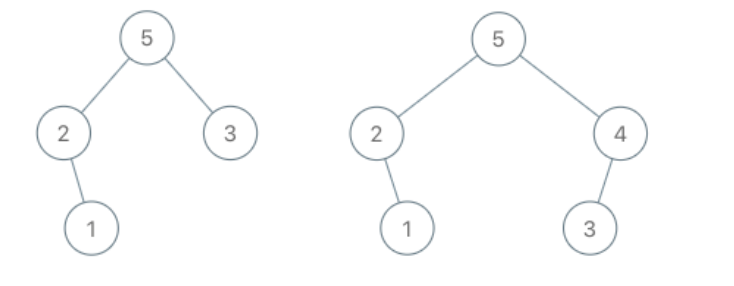
【输入】root = [5,2,3,null,1], val = 4
【输出】[5,2,4,null,1,3]
【解释】a = [2,1,5,3], b = [2,1,5,3,4]

提示：

• 树中节点数目在范围 [1, 100] 内
• 1 <= Node.val <= 100
• 树中的所有值 互不相同
• 1 <= val <= 100

三、解题思路

我猜测，当您看到这篇解题文章的时候，很大概率是因为题目描述难以理解。题目难以理解的原因，其实就在于本题与另一道题（654. 最大二叉树）是有关联的。当我们看完“654. 最大二叉树”这道题之后，再来看本题，就会非常的好理解了。

在“654. 最大二叉树”题目中，它是给出了一个数组nums，首先，将数组中最大的元素nums[i]作为根节点root，那么nums[0]到nums[i-1]都是root的左侧节点，nums[i+1]到nums[nums.length-1]都是root的右侧节点。同理，对于左侧节点和右侧节点，也是以同样的规则去创建二叉树。我们以nums=[3,2,1,6,0,5]为例，最终构建的树的过程如下所示：

那么，我们了解完“654. 最大二叉树”这道题之后，再来看本题，是不是就清晰了不少。而本题其实没有给出数组nums，给的是已经构建好的二叉树的root节点，但是其实nums和root两个结构是相辅相成的。那么，此时，我们要加入一个val值，其实也就是插入到nums数组的末尾处，也就是说，如果不考虑值的大小的话，val节点是nums中原有所有节点的右侧节点，所以我们对比遍历的路径就是root——>root.right——>root.right.right——>……。那么我们其实可以做出如下的判断：

• case1：如果val大于root.val，则root就是val节点的左子树节点。
• case2：如果val大于非root.val，则非root就是val节点的左子树节点，并且非root节点的原父节点的右子树更新为val节点。
• case3：如果val小于最底层的叶子节点，则val节点就作为该叶子节点的右子树节点。

思路我们介绍完了，下面，我们以示例3：root = [5,2,3,null,1], val = 4为例，看一下具体的操作过程。首先，我们要将4插入到二叉树中，那么，我们对比root节点node(5) > 4，所以，继续遍历node(5)的右子树node(3)，因为node(3) < 4，所以，我们创建val=4这个节点，并将node(3)作为它的左子树，即：TreeNode newNode = new TreeNode(4, node(3), null)，由于新创建的node(4)代替的node(3)原有二叉树中的位置，所以，对node(4)的原父节点node(5)的右子树进行更新，即：node(5).right = newNode；所有操作执行完毕，具体如下图所示：

解题思路就这么多了，具体的代码实现，请参见如下内容。

四、代码实现

class Solution {
    public TreeNode insertIntoMaxTree(TreeNode root, int val) {
        if (root.val < val) return new TreeNode(val, root, null);
        buildTree(root, val);
        return root;
    }
    public void buildTree(TreeNode node, int val) {
        if (node.right == null) node.right = new TreeNode(val, null, null);
        else if (node.right.val < val) node.right = new TreeNode(val, node.right, null);
        else buildTree(node.right, val);
    }
}

今天的文章内容就这些了：

写作不易，笔者几个小时甚至数天完成的一篇文章，只愿换来您几秒钟的 点赞 & 分享 。

更多技术干货，欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享，每天更新」