【广度优先搜索】leetcode 994. 腐烂的橘子

994. 腐烂的橘子

题目描述

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例1：

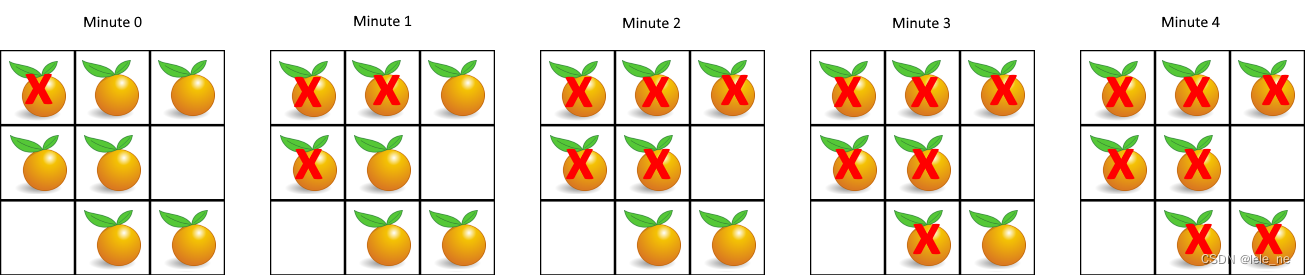
输入： grid = [[2,1,1],[1,1,0],[0,1,1]]
输出： 4

示例2：

输入： grid = [[2,1,1],[0,1,1],[1,0,1]]
输出： -1
解释： 左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例3：

输入： grid = [[0,2]]
输出： 0
解释： 因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示

• $m==grid.length$
• $n==grid[i].length$
• $1<=m,n<=10$
• $grid[i][j]仅为0、1或2$

方法：多源广度优先搜索

解题思路

观察到对于所有的腐烂橘子，其实它们在广度优先搜索上是等价于同一层的节点的。

假设这些腐烂橘子刚开始是新鲜的，而有一个腐烂橘子(我们令其为超级源点)会在下一秒把这些橘子都变腐烂，而这个腐烂橘子刚开始在的时间是 -1，那么按照广度优先搜索的算法，下一分钟也就是第 0 分钟的时候，这个腐烂橘子会把它们都变成腐烂橘子，然后继续向外拓展，所以其实这些腐烂橘子是同一层的节点。

那么在广度优先搜索的时候，我们将这些腐烂橘子都放进队列里进行广度优先搜索即可，所以最短时间 $time$ 其实是以这个超级源点的腐烂橘子为起点的广度优先遍历的层数。

在一开始保存这些腐烂橘子所在网格的下标时，同时用 $cnt1$ 统计有多少个新鲜橘子，如果为 0，则直接返回 0，因为没有新鲜的橘子可被腐烂，所以在第 0 分钟时，网格中的所有橘子已经是腐烂的了。

在广度优先搜索的过程中把已腐烂的新鲜橘子的值由 1 改为 2，最后看网格中是否由值为 1 即新鲜的橘子即可。在广度优先搜索结束后，可以记录一个变量 $cnt2$ 统计网格中的新鲜橘子数，如果 $cnt2$ 大于 0 ，说明有新鲜橘子没被腐烂，返回 −1 ，否则返回所有新鲜橘子被腐烂所需要的时间。

代码

class Solution {
public:
    const int dx[4] = {1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
    int orangesRotting(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int cnt1 = 0;
        queue<pair<int, int>> que;
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                if(grid[i][j] == 2)
                    que.push({i, j});
                else if(grid[i][j] == 1)
                    cnt1++;
        if(!cnt1)    return 0;
        int time = -1;
        while(!que.empty()) {
            time++;
            int size = que.size();
            for(int i = 0; i < size; i++) {
                auto cur = que.front();
                que.pop();
                for(int j = 0; j < 4; j++) {
                    int mx = cur.first + dx[j], my = cur.second + dy[j];
                    if(mx < 0 || mx >= m || my < 0 || my >= n || grid[mx][my] != 1)  
                        continue;
                    grid[mx][my] = 2;
                    que.push({mx, my});
                }
            }
        }
        int cnt2 = 0;
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                if(grid[i][j] == 1) 
                    cnt2++;
        return cnt2 == 0 ? time : -1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

复杂度分析

• 时间复杂度：$O(n\times m)$。
• 空间复杂度：$O(n\times m)$。