5. 吴恩达深度学习--搭建卷积神经网络模型以及应用

本文主要参考了 严宽 大神的学习笔记，并在其基础上补充了一点内容，点此查看原文。

一、神经网络的底层搭建

规定：
  上标 $[l]$ 是指第 $l$ 层。$a^{[4]}$ 是指第 4 层的激活值
  上标 $(i)$ 是指第 $l$ 个样本。$x^{(i)}$ 是指来自输入的第 i 个样本
  下标 $i$ 是指向量的第 $i$ 项。$a_i^{[4]}$ 是指第 l 层的第 i 个激活值
  $n_H^{[l]}、n_W^{[l]}、n_C^{[l]}$分别表示第 l 层的图像的高度、宽度和通道数

import numpy as np
import h5py
import matplotlib.pyplot as plt 
import tf_utils

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0)
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

#ipython很好用，但是如果在ipython里已经import过的模块修改后需要重新reload就需要这样
#在执行用户代码前，重新装入软件的扩展和模块。
%load_ext autoreload   
#autoreload 2：装入所有 %aimport 不包含的模块。
%autoreload 2          

np.random.seed(1)      #指定随机种子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

我们将搭建一个两层卷积的神经网络，卷积层其实质就是将输入转换成不同维度的输出，如下所示：

我们将一步步构建卷积层，将首先实现两个辅助函数：一个用于边界填充，一个用于计算卷积。

1. 卷积层

1.1 边界填充

边界填充将会在图像边界周围添加值为 0 的像素点，如下图所示：

使用 0 填充边界有以下好处：

• 卷积了上一层之后的 CONV 层，没有缩小高度和宽度。这对于建立更深的网络非常重要，否则在更深层时，高度/宽度会缩小。一个重要的例子是 “same” 卷积，其中高度/宽度在卷积完一层之后会被完全保留。
• 它可以帮助我们在图像边界保留更多信息。在没有填充的情况下，卷积过程中图像边缘的极少数值会受到过滤器的影响从而导致信息丢失。
  我们将实现一个边界填充函数，它会把所有的样本图像 X 都使用 0 进行填充。我们可以使用 np.pad 来快速填充。

# 填充  np.pad() 的理解
arr3D = np.array([[[1, 1, 2, 2, 3, 4],
             [1, 1, 2, 2, 3, 4], 
             [1, 1, 2, 2, 3, 4]], 
             
            [[0, 1, 2, 3, 4, 5], 
             [0, 1, 2, 3, 4, 5], 
             [0, 1, 2, 3, 4, 5]], 
             
            [[1, 1, 2, 2, 3, 4], 
             [1, 1, 2, 2, 3, 4], 
             [1, 1, 2, 2, 3, 4]]])

#((0, 0), 第一维不填充
# (1, 1), 第二维填充：上下各增加一行
# (2, 2)) 第三维填充：左右各增加两列
# 'constant'：用连续一样的值填充
print('constant:  \n' + str(np.pad(arr3D, ((0, 0), (1, 1), (2, 2)), 'constant')))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

填充结果如下：

constant:  
[[[0 0 0 0 0 0 0 0 0 0]
  [0 0 1 1 2 2 3 4 0 0]
  [0 0 1 1 2 2 3 4 0 0]
  [0 0 1 1 2 2 3 4 0 0]
  [0 0 0 0 0 0 0 0 0 0]]

 [[0 0 0 0 0 0 0 0 0 0]
  [0 0 0 1 2 3 4 5 0 0]
  [0 0 0 1 2 3 4 5 0 0]
  [0 0 0 1 2 3 4 5 0 0]
  [0 0 0 0 0 0 0 0 0 0]]

 [[0 0 0 0 0 0 0 0 0 0]
  [0 0 1 1 2 2 3 4 0 0]
  [0 0 1 1 2 2 3 4 0 0]
  [0 0 1 1 2 2 3 4 0 0]
  [0 0 0 0 0 0 0 0 0 0]]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

理解了 np.pad() 函数的用法之后，接下来我们就编写边界填充函数：

def zeros_pad(X, pad):
    """
    把数据集X的图像边界全部使用0来扩充pad个宽度和高度。
    
    参数：
        X - 图像数据集，维度为（样本数，图像高度，图像宽度，图像通道数）
        pad - 整数，每个图像在垂直和水平维度上的填充量
    返回：
        X_paded - 扩充后的图像数据集，维度为（样本数，图像高度 + 2*pad，图像宽度 + 2*pad，图像通道数）
    
    """
    
    X_paded = np.pad(X, (
                         (0, 0),      # 样本数，不填充
                         (pad, pad),  # 图像高度，上下分别填充多少行
                         (pad, pad),  # 图像宽度，左右分别填充多少列
                         (0, 0)),     # 通道数，不填充
                         'constant', constant_values=0)   # 连续一样的值填充
    return X_paded
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

测试：

np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
x_paded = zeros_pad(x, 2)
print ("x.shape =", x.shape)
print ("x_paded.shape =", x_paded.shape)
print ("x[1, 1] =", x[1, 1])
print ("x_paded[1, 1] =", x_paded[1, 1])

#绘制图
fig , axarr = plt.subplots(1,2)  #一行两列
axarr[0].set_title('x')
axarr[0].imshow(x[0,:,:,0])
axarr[1].set_title('x_paded')
axarr[1].imshow(x_paded[0,:,:,0])
1
2
3
4
5
6
7
8
9
10
11
12
13
14

测试结果如下：

x.shape = (4, 3, 3, 2)
x_paded.shape = (4, 7, 7, 2)
x[1, 1] = [[ 0.90085595 -0.68372786]
 [-0.12289023 -0.93576943]
 [-0.26788808  0.53035547]]
x_paded[1, 1] = [[0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]
 [0. 0.]]
1
2
3
4
5
6
7
8
9
10
11
12

1.2 单步卷积

在这里，我们要实现第一步卷积，需要一个过滤器来卷积输入的数据。

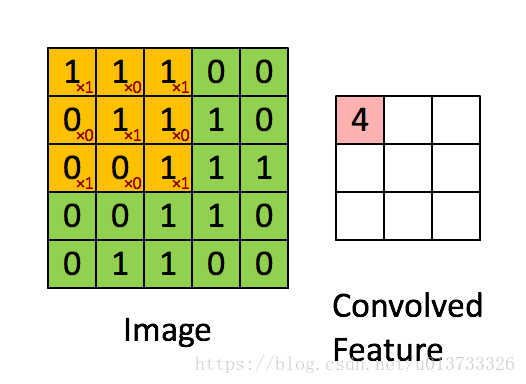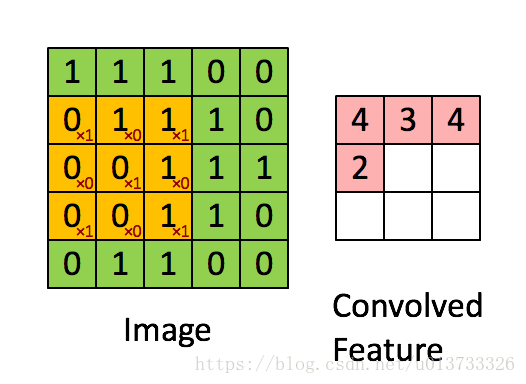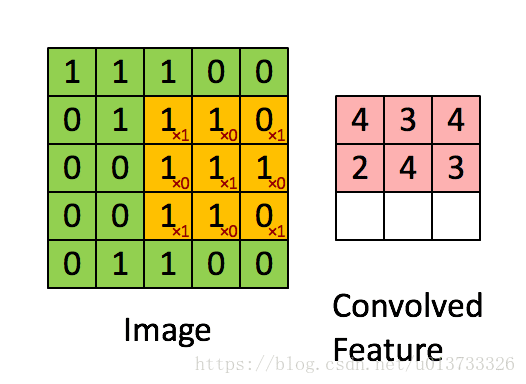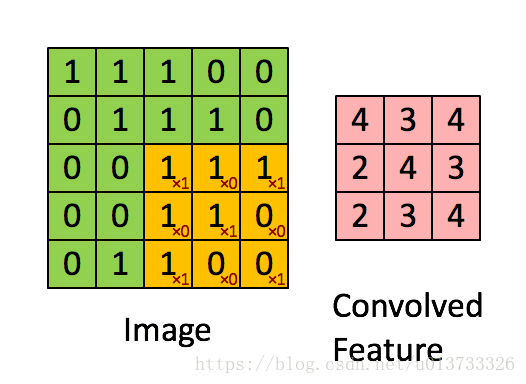
在计算机视觉应用中，左侧矩阵中的每个值都对应一个像素值，我们通过将其值与原始矩阵元素相乘（这里的相乘不是矩阵乘法，而是对应位置相乘），然后对它们进行求和来将 $3\times 3$ 过滤器与图像进行卷积。我们需要实现一个函数，将一个 $3\times 3$ 过滤器与单独的切片块进行卷积并输出一个实数。

def conv_single_step(a_slice_prev, W, b):
    """
    在前一层的激活输出的一个片段上应用一个由参数W定义的过滤器。
    这里切片大小和过滤器大小相同
    
    参数：
        a_slice_prev - 输入数据的一个片段，维度为（过滤器大小，过滤器大小，上一通道数）
        W - 权重参数，包含在了一个矩阵中，维度为（过滤器大小，过滤器大小，上一通道数）
        b - 偏置参数，包含在了一个矩阵中，维度为（1,1,1）
        
    返回：
        Z - 在输入数据的片X上卷积滑动窗口（w，b）的结果。
    """
    # 对应位置元素相乘
    s = np.multiply(a_slice_prev, W) + b
    Z = np.sum(s)
    
    return Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

测试：

np.random.seed(1)

#这里切片大小和过滤器大小相同
a_slice_prev = np.random.randn(4,4,3)
W = np.random.randn(4,4,3)
b = np.random.randn(1,1,1)

Z = conv_single_step(a_slice_prev,W,b)

print("Z = " + str(Z))     # Z = -23.16021220252078
1
2
3
4
5
6
7
8
9
10

1.3 前向传播

在前向传播的过程中，我们将使用多种过滤器对输入的数据进行卷积操作，每个过滤器会产生一个 2D 的矩阵，我们可以把它们堆叠起来，于是这些 2D 的卷积矩阵就变成了高维的矩阵。

我们需要实现一个函数以实现对激活值进行卷积，即在激活矩阵 $A_{prev}$ 上使用过滤器 $W$ 进行卷积。每个过滤器只有一个偏置 $b$。最后，我们需要一个包含了步长 $s$ 和填充 $p$ 的字典类型的超参数。
小提示：

• 如果我要在举着 $A_{prev}$（shape=（5，5，3））的左上角选择一个 $2\times 2$ 的矩阵进行切片操作，可以这样做：a_slice_prev = a_prev[0:2,0:2,:]
• 如果我想要自定义切片，我们可以这样做：先定义要切片的位置（vert_start、vert_end、horiz_start、horiz_end），如图：
  
  输出的维度的计算公式如下：$$n_H=\lfloor \frac{n_{H_{p}rev}-f+2\times pad}{stride}\rfloor +1$$$$n_W=\lfloor \frac{n_{W_{p}rev}-f+2\times pad}{stride}\rfloor +1$$其中 $n_C$ 是过滤器数量
  这里我们使用 for 循环来实现上述公式：

def conv_forward(A_prev, W, b, hparameters):
    """
    实现卷积函数的前向传播
    
    参数：
        A_prev - 上一层的激活输出矩阵，维度为(m, n_H_prev, n_W_prev, n_C_prev)，（样本数量，上一层图像的高度，上一层图像的宽度，上一层过滤器数量）
        W - 权重矩阵，维度为(f, f, n_C_prev, n_C)，（过滤器大小，过滤器大小，上一层的过滤器数量，这一层的过滤器数量）
        b - 偏置矩阵，维度为(1, 1, 1, n_C)，（1,1,1,这一层的过滤器数量）
        hparameters - 包含了"stride"与 "pad"的超参数字典。
    
    返回：
        Z - 卷积输出，维度为(m, n_H, n_W, n_C)，（样本数，图像的高度，图像的宽度，过滤器数量）
        cache - 缓存了一些反向传播函数conv_backward()需要的一些数据
    """
    
    # 获取来自上一层数据的基本信息
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # 获取权重矩阵的基本信息
    (f, f, n_C_prev, n_C) = W.shape
    
    # 获取超参数 hparameters 的值
    stride = hparameters["stride"]
    pad = hparameters["pad"]
    
    # 计算卷积后的图像的宽度和高度，参考上面的公式，使用 int() 来进行整除
    n_H = int((n_H_prev - f + 2 * pad) / stride) + 1
    n_W = int((n_W_prev - f + 2 * pad) / stride) + 1
    
    # 使用 0 来初始化卷积输出 Z
    Z = np.zeros((m, n_H, n_W, n_C))
    
    # 通过 A_prev 创建填充过了的 A_prev_pad
    A_prev_pad = zeros_pad(A_prev, pad)
    
    for i in range(m):                             # 遍历样本
        a_prev_pad = A_prev_pad[i]                 # 选择第 i 个样本的扩充后的激活矩阵
        for h in range(n_H):                       # 在输出的垂直轴上循环
            for w in range(n_W):                   # 在输出的水平轴上循环
                for c in range(n_C):               # 循环遍历输出的通道
                    # 定位当前的切片位置
                    vert_start = h * stride          # 竖向，开始的位置
                    vert_end = vert_start + f        # 竖向，结束的位置
                    horiz_start = w * stride         # 横向，开始的位置
                    horiz_end = horiz_start + f      # 横向，结束的位置
                    # 切片位置定位好了我们就把它取出来，需要注意的是我们是“穿透”取出来的
                    a_slice_prev = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
                    # 执行单步卷积
                    Z[i, h, w, c] = conv_single_step(a_slice_prev, W[:, :, :, c], b[0, 0, 0, c])
                    
    #数据处理完毕，验证数据格式是否正确
    assert(Z.shape == (m , n_H , n_W , n_C ))
    
    #存储一些缓存值，以便于反向传播使用
    cache = (A_prev,W,b,hparameters)
    
    return (Z , cache)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

测试：

np.random.seed(1)

A_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)

hparameters = {"pad" : 2, "stride": 1}

Z , cache_conv = conv_forward(A_prev,W,b,hparameters)

print("np.mean(Z) = ", np.mean(Z))
print("cache_conv[0][1][2][3] =", cache_conv[0][1][2][3])
1
2
3
4
5
6
7
8
9
10
11
12

测试结果如下：

np.mean(Z) =  0.15585932488906465
cache_conv[0][1][2][3] = [-0.20075807  0.18656139  0.41005165]
1
2

1.4 反向传播

（1） 计算 dA

$$dA=dA+\sum _{h=0}^{n_H}\sum _{w=0}^{n_W}{W}_c\times d{Z}_{hw}$$其中，$W_c$ 是过滤器，$Z_{hw}$ 是一个标量，$d{Z}_{hw}$ 是卷积层第 $h$ 行第 $w$ 列的使用点乘计算后的输出 $Z$ 的梯度。需要注意的是在每次更新 $dA$ 的时候，都会用相同的过滤器 $W_c$ 乘以不同的 $dZ$，因为在前向传播的时候，每个过滤器都与 $a_{slice}$ 进行了点乘相加，所以在计算 $dA$ 的时候，我们需要把 $a_{slice}$ 的梯度也加进来，可以在循环中加一句代码：

da_perv_pad[vert_start:vert_end,horiz_start:horiz_end,:] += W[:,:,:,c] * dZ[i,h,w,c]
1

（2）计算 dW

$$d{W}_c=d{W}_c+\sum _{h=0}^{n_H}\sum _{w=0}^{n_W}{a}_{slice}\times d{Z}_{hw}$$其中，$a_{slice}$ 对应着 $Z_{ij}$ 的激活值。由此，我们就可以推导 $W$ 的梯度，因为我们使用了过滤器来对数据进行窗口滑动，在这里我们实际上是切出了和过滤器一样大小的切片，切了多少次就产生了多少个梯度，所以我们需要把它们加起来得到这个数据集的整体 $dW$。

dW[:,:,:, c] += a_slice * dZ[i , h , w , c]
1

（3）计算 db

$$db=\sum _{h=0}^{n_H}\sum _{w=0}^{n_W}d{Z}_{hw}$$和以前的神经网络一样，$db$ 是由 $dZ$ 的累加计算的，在这里，我们只需要将卷积层的输出 $Z$ 的所有梯度累加就好了。在代码上我们只需要使用一行代码实现：

db[:,:,:,c] += dZ[i,h,w,c]
1

（4）函数实现

现在我们将实现卷积层的反向传播函数 conv_backward()，我们需要把所有的训练样本的过滤器、权值、高度、宽度都要加进来，然后使用上述公式计算对应的梯度。

def conv_backward(dZ, cache):
    """
    实现卷积层的反向传播
    
    参数：
        dZ - 卷积层的输出Z的 梯度，维度为(m, n_H, n_W, n_C)
        cache - 反向传播所需要的参数，conv_forward()的输出之一
        
    返回：
        dA_prev - 卷积层的输入（A_prev）的梯度值，维度为(m, n_H_prev, n_W_prev, n_C_prev)
        dW - 卷积层的权值的梯度，维度为(f,f,n_C_prev,n_C)
        db - 卷积层的偏置的梯度，维度为（1,1,1,n_C）
    
    """
    # 获取 cache 的值
    (A_prev, W, b, hparameters) = cache
    
    # 获取 A_prev 的基本信息
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # 获取 dZ 的基本信息
    (m, n_H, n_W, n_C) = dZ.shape
    
    # 获取权值 W 的基本信息
    (f, f, n_C_prev, n_C) = W.shape
    
    # 获取 hparameters 的值
    pad = hparameters["pad"]
    stride = hparameters["stride"]
    
    # 初始化各个梯度的结构
    dA_prev = np.zeros((m, n_H_prev, n_W_prev, n_C_prev))
    dW = np.zeros((f, f, n_C_prev, n_C))
    db = np.zeros((1, 1, 1, n_C))
    
    # 前向传播中我们使用了 pad，反向传播也需要使用，这是为了保证数据机构一致
    A_prev_pad = zeros_pad(A_prev, pad)
    dA_prev_pad = zeros_pad(dA_prev, pad)
    
    # 现在处理数据
    for i in range(m):
        # 选择第 i 个扩充了的数据样本， 降了一维
        a_prev_pad = A_prev_pad[i]
        da_prev_pad = dA_prev_pad[i]
        
        for h in range(n_H):
            for w in range(n_W):
                for c in range(n_C):
                    # 定位切片位置
                    vert_start = h
                    vert_end = vert_start + f
                    horiz_start = w
                    horiz_end = horiz_start + f
                    
                    #定位完毕，开始切片
                    a_slice = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]
                    
                    #切片完毕，使用上面的公式计算梯度
                    da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:, :, :, c] * dZ[i, h, w, c]
                    dW[:, :, :, c] += a_slice * dZ[i, h, w, c]
                    db[:, :, :, c] += dZ[i, h, w, c]
                    
        # 设置第 i 个样本最终的 dA_prev，即把非填充的数据取出来
        dA_prev[i, :, :, :] = da_prev_pad[pad: -pad, pad: -pad, :]
    
     #数据处理完毕，验证数据格式是否正确
    assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
    
    return (dA_prev,dW,db)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

测试：

np.random.seed(1)
#初始化参数
A_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)
hparameters = {"pad" : 2, "stride": 1}

#前向传播
Z , cache_conv = conv_forward(A_prev,W,b,hparameters)
#反向传播
dA , dW , db = conv_backward(Z,cache_conv)
print("dA_mean =", np.mean(dA))
print("dW_mean =", np.mean(dW))
print("db_mean =", np.mean(db))
1
2
3
4
5
6
7
8
9
10
11
12
13
14

测试结果如下：

dA_mean = 9.608990675868995
dW_mean = 10.581741275547566
db_mean = 76.37106919563735
1
2
3

5. 池化层

池化层是 CNN 中用来减小尺寸，提高运算速度的，同样能减小 noise 影响，让各特征更具有健壮性。有两种做法：
（1）最大值池化层：在过滤器算子滑动区域内取最大值。这样可以只保留区域内的最大值，降低 noise 影响。

（2）平均池化层：在过滤器算子滑动区域内取计算平均值

5.1 前向传播

现在我们要在同一个函数中实现 最大值池化层 和 均值池化层，和之前计算输出维度一样，池化层的计算也是一样的。$$n_H=\lfloor \frac{n_{H_{prev}}-f}{strid}\rfloor +1$$$$n_W=\lfloor \frac{n_{W_{prev}}-f}{strid}\rfloor +1$$$$n_C=n_{C_{prev}}$$

def pool_forward(A_prev, hparameters, mode="max"):
    """
    实现池化层的前向传播
    
    参数：
        A_prev - 输入数据，维度为(m, n_H_prev, n_W_prev, n_C_prev)
        hparameters - 包含了 "f" 和 "stride"的超参数字典
        mode - 模式选择【"max" | "average"】
        
    返回：
        A - 池化层的输出，维度为 (m, n_H, n_W, n_C)
        cache - 存储了一些反向传播需要用到的值，包含了输入和超参数的字典。
    """
    # 获取输入数据的基本信息
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # 获取超参数的信息
    f = hparameters["f"]
    stride = hparameters["stride"]
    
    # 计算输出维度
    n_H = int((n_H_prev - f) / stride) + 1
    n_W = int((n_W_prev - f) / stride) + 1
    n_C = n_C_prev
    
    # 初始化输出矩阵
    A = np.zeros((m, n_H, n_W, n_C))
    
    for i in range(m):                              #遍历样本
        for h in range(n_H):                        #在输出的垂直轴上循环
            for w in range(n_W):                    #在输出的水平轴上循环
                for c in range(n_C):                #循环遍历输出的通道
                    #定位当前的切片位置
                    vert_start = h * stride         #竖向，开始的位置
                    vert_end = vert_start + f       #竖向，结束的位置
                    horiz_start = w * stride        #横向，开始的位置
                    horiz_end = horiz_start + f     #横向，结束的位置
                    #定位完毕，开始切割
                    a_slice_prev = A_prev[i,vert_start:vert_end,horiz_start:horiz_end,c]
                    
                    #对切片进行池化操作
                    if mode == "max":
                        A[ i , h , w , c ] = np.max(a_slice_prev)
                    elif mode == "average":
                        A[ i , h , w , c ] = np.mean(a_slice_prev)
                        
    #池化完毕，校验数据格式
    assert(A.shape == (m , n_H , n_W , n_C))
    
    #校验完毕，开始存储用于反向传播的值
    cache = (A_prev,hparameters)
    
    return A,cache
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

测试：

np.random.seed(1)
A_prev = np.random.randn(2,4,4,3)
hparameters = {"f":4 , "stride":1}

A , cache = pool_forward(A_prev,hparameters,mode="max")
print("mode = max")
print("A =", A)
print("----------------------------")
A, cache = pool_forward(A_prev, hparameters, mode = "average")
print("mode = average")
print("A =", A)
1
2
3
4
5
6
7
8
9
10
11

测试结果如下：

mode = max
A = [[[[1.74481176 1.6924546  2.10025514]]]

 [[[1.19891788 1.51981682 2.18557541]]]]
----------------------------
mode = average
A = [[[[-0.09498456  0.11180064 -0.14263511]]]

 [[[-0.09525108  0.28325018  0.33035185]]]]
1
2
3
4
5
6
7
8
9

5.2 反向传播

接下来，我们从最大值池化层开始实现池化层的反向传播，即使池化层没有反向传播过程中要更新的参数，我们仍然要通过池化层反向传播梯度，以便为在池化层之前的层（如卷积层）计算梯度。
（1）最大池化层的反向传播
在开始池化层的反向传播之前，我们需要创建一个 create_mask_from_window() 的函数，它会创建一个掩码矩阵来保存最大值的位置，当为 1 的时候表示最大值的位置，其他的为 0。如：
X = [ 1 3 4 2 ] → M = [ 0 0 1 0 ] X=\left[

\right]\rightarrow M=\left[ \right] X=[14​32​]→M=[01​00​]

def create_mask_from_window(x):
    """
    从输入矩阵中创建掩码，以保存最大值的矩阵的位置。
    
    参数：
        x - 一个维度为(f,f)的矩阵
        
    返回：
        mask - 包含x的最大值的位置的矩阵
    """
    mask = x == np.max(x)
    return mask
1
2
3
4
5
6
7
8
9
10
11
12

测试：

np.random.seed(1)

x = np.random.randn(2,3)

mask = create_mask_from_window(x)

print("x = " + str(x)) 
print("mask = " + str(mask))
1
2
3
4
5
6
7
8

测试结果如下：

x = [[ 1.62434536 -0.61175641 -0.52817175]
 [-1.07296862  0.86540763 -2.3015387 ]]
mask = [[ True False False]
 [False False False]]
1
2
3
4

为什么我们要创建这个掩码矩阵呢？是因为如果我们不记录最大值的位置，那么无法从池化层反向传播到卷积层。
（2）平均池化层的反向传播
在最大值池化层中，对于每个输入窗口，输出的所有值都来自输入中的最大值，但是在平均池化层中，因为是计算均值，所以输入窗口的每个元素对输出有一样的影响。
d Z = 1 → d Z = [ 1 4 1 4 1 4 1 4 ] dZ = 1 \rightarrow dZ=\left[

\right] dZ=1→dZ=[41​41​​41​41​​]

def distribute_value(dz, shape):
    """
    给定一个值，按矩阵大小平均分配到每一个矩阵位置中。
    
    参数：
        dz - 输入的实数
        shape - 元组，两个值，分别为n_H , n_W
        
    返回：
        a - 已经分配好了值的矩阵，里面的值全部一样。
    
    """
    # 获取矩阵的大小
    (n_H, n_W) = shape
    
    # 计算平均值
    average = dz / (n_H * n_W)
    
    # 填充入矩阵
    a = np.ones(shape) * average
    
    return a
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

测试：

dz = 2
shape = (2,2)

a = distribute_value(dz,shape)
print("a = " + str(a))
1
2
3
4
5

测试结果如下：

a = [[0.5 0.5]
 [0.5 0.5]]
1
2

（3）池化层的反向传播

def pool_backward(dA, cache, mode="max"):
    """
    实现池化层的反向传播
    
    参数:
        dA - 池化层的输出的梯度，和池化层的输出的维度一样
        cache - 池化层前向传播时所存储的参数。
        mode - 模式选择，【"max" | "average"】
        
    返回：
        dA_prev - 池化层的输入的梯度，和A_prev的维度相同
    
    """
    # 获取 cache 中的值
    (A_prev, hparameters) = cache
    
    # 获取 hparameters 的值
    f = hparameters["f"]
    stride = hparameters["stride"]
    
    # 获取 A_prev 和 dA 的基本信息
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    (m, n_H, n_W, n_C) = dA.shape
    
    # 初始化输出的结构
    dA_prev = np.zeros_like(A_prev)
    
    # 开始处理数据
    for i in range(m):
        a_prev = A_prev[i]
        for h in range(n_H):
            for w in range(n_W):
                for c in range(n_C):
                    # 定位切片位置
                    vert_start = h
                    vert_end = vert_start + f
                    horiz_start = w
                    horiz_end = horiz_start + f
                    
                    #选择反向传播的计算方式
                    if mode == "max":
                        #开始切片
                        a_prev_slice = a_prev[vert_start:vert_end,horiz_start:horiz_end,c]
                        #创建掩码
                        mask = create_mask_from_window(a_prev_slice)
                        #计算dA_prev
                        dA_prev[i,vert_start:vert_end,horiz_start:horiz_end,c] += np.multiply(mask,dA[i,h,w,c])
    
                    elif mode == "average":
                        #获取dA的值
                        da = dA[i,h,w,c]
                        #定义过滤器大小
                        shape = (f,f)
                        #平均分配
                        dA_prev[i,vert_start:vert_end, horiz_start:horiz_end ,c] += distribute_value(da,shape)
    #数据处理完毕，开始验证格式
    assert(dA_prev.shape == A_prev.shape)
    
    return dA_prev
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

测试：

np.random.seed(1)
A_prev = np.random.randn(5, 5, 3, 2)
hparameters = {"stride" : 1, "f": 2}
A, cache = pool_forward(A_prev, hparameters)
dA = np.random.randn(5, 4, 2, 2)

dA_prev = pool_backward(dA, cache, mode = "max")
print("mode = max")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1])  
print()
dA_prev = pool_backward(dA, cache, mode = "average")
print("mode = average")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1]) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

测试结果如下：

mode = max
mean of dA =  0.14571390272918056
dA_prev[1,1] =  [[ 0.          0.        ]
 [ 5.05844394 -1.68282702]
 [ 0.          0.        ]]

mode = average
mean of dA =  0.14571390272918056
dA_prev[1,1] =  [[ 0.08485462  0.2787552 ]
 [ 1.26461098 -0.25749373]
 [ 1.17975636 -0.53624893]]
1
2
3
4
5
6
7
8
9
10
11

二、神经网络的应用

我们已经使用了原生代码实现了卷积神经网络，现在我们要使用 Tensorflow 来实现，然后应用到手势识别中，在这里我们要实现 4 个函数。

import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import tensorflow as tf
from tensorflow.python.framework import ops

import cnn_utils

%matplotlib inline
np.random.seed(1)
1
2
3
4
5
6
7
8
9
10
11
12

读入数据集

X_train_orig , Y_train_orig , X_test_orig , Y_test_orig , classes = tf_utils.load_dataset()
1

看一下样例图片：

index = 6
plt.imshow(X_train_orig[index])
print ("y = " + str(np.squeeze(Y_train_orig[:, index])))
1
2
3

one-hot 编码

将数据进行处理，并转化为 one-hot 编码

# 归一化处理
X_train = X_train_orig/255.
X_test = X_test_orig/255.

# 转化为 独热编码
Y_train = cnn_utils.convert_to_one_hot(Y_train_orig, 6).T
Y_test = cnn_utils.convert_to_one_hot(Y_test_orig, 6).T

print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
conv_layers = {}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

输出结果如下：

number of training examples = 1080
number of test examples = 120
X_train shape: (1080, 64, 64, 3)
Y_train shape: (1080, 6)
X_test shape: (120, 64, 64, 3)
Y_test shape: (120, 6)
1
2
3
4
5
6

1. 创建 placeholders

Tensorflow 要求您为运行会话时将输入到模型中的输入数据创建占位符。现在我们要实现创建占位符的函数，因为我们使用的是小批量数据块，输入的样本数量可能不固定，所以我们在数量那里要使用 None 作为可变数量。输入 X 的维度为 [None, n_H0, n_W0, n_C0]，对应的 Y 的维度为 [None, n_y]。

tf.compat.v1.disable_v2_behavior()   # 使tf2.0的行为失效
def create_placeholders(n_H0, n_W0, n_C0, n_y):
    """
    为session创建占位符
    
    参数：
        n_H0 - 实数，输入图像的高度
        n_W0 - 实数，输入图像的宽度
        n_C0 - 实数，输入的通道数
        n_y  - 实数，分类数
        
    输出：
        X - 输入数据的占位符，维度为[None, n_H0, n_W0, n_C0]，类型为"float"
        Y - 输入数据的标签的占位符，维度为[None, n_y]，维度为"float"
    """
    X = tf.compat.v1.placeholder(tf.float32, [None, n_H0, n_W0, n_C0])
    Y = tf.compat.v1.placeholder(tf.float32, [None, n_y])
    
    return X, Y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

测试：

X , Y = create_placeholders(64,64,3,6)
print ("X = " + str(X))
print ("Y = " + str(Y))
1
2
3

测试结果如下：

X = Tensor("Placeholder:0", shape=(?, 64, 64, 3), dtype=float32)
Y = Tensor("Placeholder_1:0", shape=(?, 6), dtype=float32)
1
2

2. 初始化参数

现在我们将使用 tf.keras.initializers.glorot_normal(seed=0) 来初始化权值/过滤器 $W1、W2$。在这里，我们不需要考虑偏置，因为 Tensorflow 会考虑到的。需要注意的是我们只需要初始化 2D卷积函数，全连接层 Tensorflow会自动初始化。

def initialize_parameters():
    """
    初始化权值矩阵，这里我们把权值矩阵硬编码：
    W1 : [4, 4, 3, 8]
    W2 : [2, 2, 8, 16]
    
    返回：
        包含了tensor类型的W1、W2的字典
    """
    tf.compat.v1.set_random_seed(1)
    
    W1 = tf.compat.v1.get_variable("W1", [4, 4, 3, 8], initializer=tf.keras.initializers.glorot_normal(seed=0))
    W2 = tf.compat.v1.get_variable("W2", [2, 2, 8, 16], initializer=tf.keras.initializers.glorot_normal(seed=0))
    
    parameters = {"W1": W1, "W2": W2}
    
    return parameters
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

测试：

ops.reset_default_graph()
with tf.compat.v1.Session() as sess_test:
    parameters = initialize_parameters()
    init = tf.compat.v1.global_variables_initializer()
    sess_test.run(init)
    print("W1 = " + str(parameters["W1"].eval()[1, 1, 1]))
    print("W2 = " + str(parameters["W2"].eval()[1, 1, 1]))
    
    sess_test.close()
1
2
3
4
5
6
7
8
9

测试结果如下：

W1 = [ 0.03393849 -0.16554174 -0.006313    0.01852748 -0.03301779 -0.03344928
 -0.14225453  0.13832784]
W2 = [ 0.18496291 -0.17294659 -0.22462192 -0.00193902 -0.12594481  0.02987488
 -0.23320328 -0.23961914  0.14771584  0.09277791  0.01622899  0.24536026
 -0.12588692 -0.32413897 -0.21403536 -0.17823085]
1
2
3
4
5

3. 前向传播

在实现前向传播时 Tensorflow 里面有一些可以直接用的函数：

• tf.nn.conv2d(X,W1,strides=[1,s,s,1],padding='SAME')：给定输入 $X$ 和一组过滤器 $W1$，这个函数将会自动使用 $W1$ 来对 $X$ 进行卷积，第三个输入参数 [1,s,s,1] 是指对于输入 (m, n_H_prev, n_W_prev, n_C_prev) 而言，每次滑动的步伐。
• tf.nn.max_pool(A, ksize = [1,f,f,1], strides = [1,s,s,1], padding = 'SAME')：给定输入 $X$，该函数将会使用大小为 $(f,f)$ 以及步伐为 $(s,s)$ 的窗口对其进行滑动取最大值。
• tf.nn.relu(Z1)：计算 $Z1$ 的 ReLU 激活。
• tf.compat.v1.layers.flatten(P)：给定一个输入 $P$，此函数将会把每个样本转化成一维的向量，然后返回一个 tensor 变量，其维度为 (batch_size, k)。
• tf.compat.v1.layers.dense(F, 6, activation=None)：给定一个已经一维化了的输入 $F$，此函数将会返回一个由全连接层计算过后的输出。
  全连接层会自动初始化权值且在训练模型的时候会一直参与，所以我们不需要专门去初始化它的权值。
  在实现前向传播的时候，需要定义一下模型的大概样子：
  $$CONV2D\to RELU\to MAXPOOL\to CONV2D\to RELU\to MAXPOOL\to FULLCONNECTED$$我们具体实现的时候，使用如下的步骤和参数：
• Conv2d：步伐：1，填充方式：SAME
• ReLU
• MAX POOLING：过滤器大小：$8\times 8$，步伐：$8\times 8$，填充方式：SAME
• Conv2d：步伐：1，填充方式：SAME
• ReLU
• MAX POOLING：过滤器大小：$4\times 4$，步伐：$4\times 4$，填充方式：SAME
• FLATTEN
• FC：使用没有非线性激活函数的全连接层。这里不要调用 Softmax。 在 TensorFlow 中，Softmax 和 cost 函数被集中到一个函数中。

def forward_propagation(X, parameters):
    """
    实现前向传播
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
    
    参数：
        X - 输入数据的placeholder，维度为(输入节点数量，样本数量)
        parameters - 包含了“W1”和“W2”的python字典。
        
    返回：
        Z3 - 最后一个LINEAR节点的输出
    
    """
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    
    # Conv2d：步伐：1，填充方式：“SAME”
    Z1 = tf.nn.conv2d(X, W1, strides=[1,1,1,1], padding="SAME")
    # ReLU
    A1 = tf.nn.relu(Z1)
    # Max pool：窗口大小：8x8，填充方式：“SAME”
    P1 = tf.nn.max_pool(A1, ksize=[1,8,8,1], strides=[1,8,8,1], padding="SAME")
    
    # Conv2d：步伐：1，填充方式：“SAME”
    Z2 = tf.nn.conv2d(P1, W2, strides=[1,1,1,1],padding="SAME")
    # ReLU
    A2 = tf.nn.relu(Z2)
    # Max pool：过滤器大小：4x4，步伐：4x4，填充方式：“SAME”
    P2 = tf.nn.max_pool(A2, ksize=[1,4,4,1], strides=[1,4,4,1], padding="SAME")
    
    # 一维化上一层的输出
    P = tf.compat.v1.layers.flatten(P2)
    
    # 全连接层（FC）：使用没有非线性激活函数的全连接层
    Z3 = tf.compat.v1.layers.dense(P, 6, activation=None)
    
    return Z3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

测试：

ops.reset_default_graph()
np.random.seed(1)

with tf.compat.v1.Session() as sess_test:
    X, Y = create_placeholders(64, 64, 3, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)
    
    init = tf.compat.v1.global_variables_initializer()
    sess_test.run(init)
    
    a = sess_test.run(Z3, {X:np.random.randn(2, 64, 64, 3), Y:np.random.randn(2, 6)})
    print("Z3 = " + str(a))
    
    sess_test.close()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

测试结果如下：

Z3 = [[ 0.9405632   0.37512606  1.2375003   0.09332052  0.2361663  -1.1231548 ]
 [ 1.2040255   0.4606552   1.3588419  -0.03463529  0.11202908 -1.1748538 ]]
1
2

4. 计算成本

我们实现计算成本，需要用到下面两个函数：

• tf.nn.softmax_cross_entropy_with_logits(logits = Z3 , lables = Y)：既计算 Softmax 的激活，也计算其损失。
• tf.reduce_mean：计算平均值，使用它来计算所有样本的损失来得到总成本。

def compute_cost(Z3, Y):
    """
    计算成本
    参数：
        Z3 - 正向传播最后一个LINEAR节点的输出，维度为（6，样本数）。
        Y - 标签向量的placeholder，和Z3的维度相同
    
    返回：
        cost - 计算后的成本
    
    """
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=Z3, labels=Y))
    
    return cost
1
2
3
4
5
6
7
8
9
10
11
12
13
14

测试：

ops.reset_default_graph()

with tf.compat.v1.Session() as sess_test:
    np.random.seed(1)
    X, Y = create_placeholders(64, 64, 3, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)
    cost = compute_cost(Z3, Y)
    
    init = tf.compat.v1.global_variables_initializer()
    sess_test.run(init)
    
    a = sess_test.run(cost, {X:np.random.randn(4, 64, 64, 3), Y:np.random.randn(4, 6)})
    print("cost = " + str(a))
    
    sess_test.close()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

测试结果如下：

cost = 0.79182863
1

5. 构建模型

模型所做的工作如下：

• 创建占位符
• 初始化参数
• 前向传播
• 计算成本
• 反向传播
• 创建优化器

def model(X_train, Y_train, X_test, Y_test, learning_rate=0.005,
          num_epochs=100, minibatch_size=64, print_cost=True, isPlot=True):
    """
    使用TensorFlow实现三层的卷积神经网络
    CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
    
    参数：
        X_train - 训练数据，维度为(None, 64, 64, 3)
        Y_train - 训练数据对应的标签，维度为(None, n_y = 6)
        X_test - 测试数据，维度为(None, 64, 64, 3)
        Y_test - 训练数据对应的标签，维度为(None, n_y = 6)
        learning_rate - 学习率
        num_epochs - 遍历整个数据集的次数
        minibatch_size - 每个小批量数据块的大小
        print_cost - 是否打印成本值，每遍历100次整个数据集打印一次
        isPlot - 是否绘制图谱
        
    返回：
        train_accuracy - 实数，训练集的准确度
        test_accuracy - 实数，测试集的准确度
        parameters - 学习后的参数
    """
    ops.reset_default_graph()         # 能够重新运行模型而不覆盖 tf 变量
    tf.compat.v1.set_random_seed(1)   # 设置随机数种子
    seed = 3
    (m, n_H0, n_W0, n_C0) = X_train.shape
    n_y = Y_train.shape[1]
    costs = []
    
    # 为当前维度创建占位符
    X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)
    
    # 初始化参数
    parameters = initialize_parameters()
    
    # 前向传播
    Z3 = forward_propagation(X, parameters)
    
    # 计算成本
    cost = compute_cost(Z3, Y)
    
    # 反向传播，由于框架已经实现了反向传播，我们只需要选择一个优化器就行了
    optimizer = tf.compat.v1.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
    
    # 全局初始化所有变量
    init = tf.compat.v1.global_variables_initializer()
    
    # 开始运行
    with tf.compat.v1.Session() as sess:
        # 初始化参数
        sess.run(init)
        # 开始遍历数据集
        for epoch in range(num_epochs):
            minibatch_cost = 0
            num_minibatches = int(m / minibatch_size)  # 获取数据块的数量
            seed += 1
            minibatches = cnn_utils.random_mini_batches(X_train, Y_train, minibatch_size, seed)
            
            # 对每个数据块进行处理
            for minibatch in minibatches:
                # 选择一个数据块
                (minibatch_X, minibatch_Y) = minibatch
                # 最小化这个数据块的成本
                _, temp_cost, temp_parameters = sess.run([optimizer, cost, parameters], feed_dict={X:minibatch_X, Y:minibatch_Y})
                
                # 累加数据块的成本值
                minibatch_cost += temp_cost / num_minibatches
                
            #是否打印成本
            if print_cost:
                #每5代打印一次
                if epoch % 5 == 0:
                    print("当前是第 " + str(epoch) + " 代，成本值为：" + str(minibatch_cost))
            
            #记录成本
            if epoch % 1 == 0:
                costs.append(minibatch_cost)
        
        #数据处理完毕，绘制成本曲线
        if isPlot:
            plt.plot(np.squeeze(costs))
            plt.ylabel('cost')
            plt.xlabel('iterations (per tens)')
            plt.title("Learning rate =" + str(learning_rate))
            plt.show()
        
        # 开始预测数据
        ## 计算当前的预测情况
        predict_op = tf.compat.v1.arg_max(Z3, 1)
        corrent_prediction = tf.equal(predict_op, tf.compat.v1.arg_max(Y, 1))
        
        ## 计算准确度
        accuracy = tf.reduce_mean(tf.cast(corrent_prediction, "float"))
        print("corrent_prediction accuracy= " + str(accuracy))
        
        train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
        test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
        
        print("训练集准确度：" + str(train_accuracy))
        print("测试集准确度：" + str(test_accuracy))
        
        return (train_accuracy, test_accuracy, temp_parameters)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102

训练模型：

_, _, parameters = model(X_train, Y_train, X_test, Y_test,num_epochs=150)
1

训练结果如下：

当前是第 0 代，成本值为：1.9082637503743172
当前是第 5 代，成本值为：1.5873964205384254
当前是第 10 代，成本值为：1.0073989257216454
当前是第 15 代，成本值为：0.7799001224339008
当前是第 20 代，成本值为：0.5975085962563753
当前是第 25 代，成本值为：0.5086729153990746
当前是第 30 代，成本值为：0.4312992487102747
当前是第 35 代，成本值为：0.37938646227121353
当前是第 40 代，成本值为：0.39569839648902416
当前是第 45 代，成本值为：0.32816184870898724
当前是第 50 代，成本值为：0.26437038742005825
当前是第 55 代，成本值为：0.2620638655498624
当前是第 60 代，成本值为：0.23943777661770582
当前是第 65 代，成本值为：0.20767591940239072
当前是第 70 代，成本值为：0.18899284722283483
当前是第 75 代，成本值为：0.18479297868907452
当前是第 80 代，成本值为：0.18045786954462528
当前是第 85 代，成本值为：0.1472180988639593
当前是第 90 代，成本值为：0.1306172339245677
当前是第 95 代，成本值为：0.12501105340197682
当前是第 100 代，成本值为：0.12093653716146946
当前是第 105 代，成本值为：0.1363647971302271
当前是第 110 代，成本值为：0.10240168101154268
当前是第 115 代，成本值为：0.10396354575641453
当前是第 120 代，成本值为：0.11999449389986694
当前是第 125 代，成本值为：0.09466223162598908
当前是第 130 代，成本值为：0.07958365138620138
当前是第 135 代，成本值为：0.06703681370709091
当前是第 140 代，成本值为：0.08233092306181788
当前是第 145 代，成本值为：0.06252288771793246
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30