• C++/Python:罗德里格斯旋转矩阵

    背景：给定两个向量V1,V2，怎么求之间的转换矩阵?

    [羽量级公司发月饼了，比去年强，手提式的了\dog]

    1、求旋转轴

    通过V1和V2的叉积，可以知道旋转轴Vcross（垂直屏幕指向外侧或内侧的向量）

    vcross = np.cross(v1, v2)

    这里还可以将旋转轴向量单位化，方便后面使用

    vcross_normalize = 1 / np.linalg.norm(vcross) * vcross

     2、求旋转角度

    还可以知道两向量的夹角（这个夹角是沿着旋转轴的角度，因为两向量确定了一个平面，而旋转轴是垂直平面的）

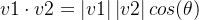
    v1\cdot v2=\left | v1 \right |\left | v2 \right |cos(\theta )

    \theta =arccos[(v1\cdot v2)/\left | v1 \right |\left | v2 \right |]

    theta = math.acos(v1.dot(v2)/(np.linalg.norm(v1)*np.linalg.norm(v2)))

     3、求旋转矩阵

    知道了旋转轴以及旋转角度，就可以祭出罗德里格斯(Rodriguez)公式了，可以直接代入得出旋转矩阵

    R_{vcrossnorm}(\theta )=\begin{bmatrix} cos(\theta )+v_{x}^{2} (1-cos(\theta ))&v_{x}v_{y}(1-cos(\theta))-v_{z}sin(\theta) &v_{y}sin(\theta)+v_{x}v_{z}(1-cos(\theta)) \\ v_{z}sin(\theta)+v_{x}v_{y}(1-cos(\theta))&cos(\theta )+v_{y}^{2} (1-cos(\theta )) & -v_{x}sin(\theta)+v_{y}v_{z}(1-cos(\theta)) \\ -v_{y}sin(\theta)+v_{x}v_{z}(1-cos(\theta)) &v_{x}sin(\theta)+v_{y}v_{z}(1-cos(\theta)) & cos(\theta )+v_{z}^{2} (1-cos(\theta )) \end{bmatrix}

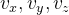     上式中的v_{x}, v_{y},v_{z}分别指单位化后的旋转轴向量vcross_normalize的xyz

    1. Rot = np.zeros((3, 3), dtype=np.float32)
    2. Rot[0][0] = math.cos(theta)+(1-math.cos(theta))*(vcross_normalize[0]**2)
    3. Rot[0][1] = vcross_normalize[0]*vcross_normalize[1]*(1-math.cos(theta))-vcross_normalize[2]*math.sin(theta)
    4. Rot[0][2] = vcross_normalize[1]*math.sin(theta)+vcross_normalize[0]*vcross_normalize[2]*(1-math.cos(theta))
    5. Rot[1][0] = vcross_normalize[2]*math.sin(theta)+vcross_normalize[0]*vcross_normalize[1]*(1-math.cos(theta))
    6. Rot[1][1] = math.cos(theta)+(1-math.cos(theta))*(vcross_normalize[1]**2)
    7. Rot[1][2] = -vcross_normalize[0] * math.sin(theta) + vcross_normalize[1] * vcross_normalize[2] * (
    8.             1 - math.cos(theta))
    9. Rot[2][0] = -vcross_normalize[1] * math.sin(theta) + vcross_normalize[0] * vcross_normalize[2] * (
    10.         1 - math.cos(theta))
    11. Rot[2][1] = vcross_normalize[0] * math.sin(theta) + vcross_normalize[1] * vcross_normalize[2] * (
    12.         1 - math.cos(theta))
    13. Rot[2][2] = math.cos(theta) + (1 - math.cos(theta)) * (vcross_normalize[2] ** 2)
    14.  
    15. R = np.matrix(Rot)  # 转为矩阵方便后续运算

    这样，就求出了旋转矩阵R。 

    4、验证

    毕竟这里没有推导，拿过来就用，多少有点犯嘀咕，那就验证一下吧。

    旋转后的点=R*旋转前的点

    旋转前的点 = 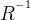R^{^{-1}}*旋转后的点

    预期效果：

     假如在水平方向有一条线，所有点的y坐标都相同，顺时针旋转45度后，所有点的y坐标应该是一个等差的，斜率为-1。（此时的两个向量v1，v2分别取（0,1,0）和（1,1,0），刚好是45度）

    测试结果：

    1. import matplotlib.pyplot as plt
    2. import mpl_toolkits.axisartist as axisartist
    3. import cv2
    4. import math
    5. import numpy as np
    6.  
    7. norm_wall = np.array([0, 1, 0],dtype=np.float32)
    8. norm_pro = np.array([1,1,0],dtype=np.float32)
    9.  
    10. theta = math.acos(norm_wall.dot(norm_pro)/(np.linalg.norm(norm_wall)*np.linalg.norm(norm_pro)))
    11. vcross = np.cross(norm_wall, norm_pro)
    12. print(vcross)
    13. vcross_normalize = 1 / np.linalg.norm(vcross) * vcross
    14. print(vcross_normalize)
    15. Rot = np.zeros((3, 3), dtype=np.float32)
    16. Rot[0][0] = math.cos(theta)+(1-math.cos(theta))*(vcross_normalize[0]**2)
    17. Rot[0][1] = vcross_normalize[0]*vcross_normalize[1]*(1-math.cos(theta))-vcross_normalize[2]*math.sin(theta)
    18. Rot[0][2] = vcross_normalize[1]*math.sin(theta)+vcross_normalize[0]*vcross_normalize[2]*(1-math.cos(theta))
    19. Rot[1][0] = vcross_normalize[2]*math.sin(theta)+vcross_normalize[0]*vcross_normalize[1]*(1-math.cos(theta))
    20. Rot[1][1] = math.cos(theta)+(1-math.cos(theta))*(vcross_normalize[1]**2)
    21. Rot[1][2] = -vcross_normalize[0] * math.sin(theta) + vcross_normalize[1] * vcross_normalize[2] * (
    22.             1 - math.cos(theta))
    23. Rot[2][0] = -vcross_normalize[1] * math.sin(theta) + vcross_normalize[0] * vcross_normalize[2] * (
    24.         1 - math.cos(theta))
    25. Rot[2][1] = vcross_normalize[0] * math.sin(theta) + vcross_normalize[1] * vcross_normalize[2] * (
    26.         1 - math.cos(theta))
    27. Rot[2][2] = math.cos(theta) + (1 - math.cos(theta)) * (vcross_normalize[2] ** 2)
    28.  
    29. R = np.matrix(Rot)
    30.  
    31. p_arr = []
    32. for i in range(20):
    33.     x = i-10
    34.     y = 10
    35.     p_arr.append([x,y,0])
    36.  
    37. p_out = []
    38. for p in p_arr:
    39.     tmp = R*np.matrix(p).T
    40.     p_out.append(tmp)
    41.  
    42. ################
    43. fig = plt.figure(figsize=(80, 80))  # 创建画布
    44. #使用axisartist.Subplot方法创建一个绘图区对象ax
    45. ax = axisartist.Subplot(fig, 111)  # 111 代表1行1列的第1个，subplot()可以用于绘制多个子图
    46. fig.add_axes(ax)  # 将绘图区对象添加到画布中
    47. # ----------2. 绘制带箭头的x-y坐标轴#通过set_visible方法设置绘图区所有坐标轴隐藏-------
    48. ax.axis[:].set_visible(False)  # 隐藏了四周的方框
    49. #ax.new_floating_axis代表添加新的坐标轴
    50. ax.axis["x"] = ax.new_floating_axis(0,0)
    51. ax.axis["x"].set_axisline_style("->", size = 1.0)  # 给x坐标轴加上箭头
    52. ax.axis["y"] = ax.new_floating_axis(1,0)  # 添加y坐标轴，且加上箭头
    53. ax.axis["y"].set_axisline_style("-|>", size = 1.0)
    54. #设置x、y轴上刻度显示方向
    55. ax.axis["x"].set_axis_direction("top")
    56. ax.axis["y"].set_axis_direction("right")
    57. ##################
    58.  
    59. ##画原始点
    60. p_arr = np.array(p_arr)
    61. plt.plot(p_arr[:,0],p_arr[:,1],color='red')
    62. ''' 设置x轴的刻度：plt.xlim() '''
    63. plt.xlim(-20,20)   # 设置x轴的刻度从-2到12
    64. ''' 设置y轴的刻度：plt.ylim() '''
    65. plt.ylim(-2,20)    # 设置x轴的刻度从2到10
    66. ##画旋转后的点
    67. p_out = np.array(p_out)
    68. plt.plot(p_out[:,0],p_out[:,1],color='blue')
    69. plt.show()

     5、验证2

    上面是正向验证，在反向验证一下，给一些斜线上的点比如y=-0.5x+10，将其旋转到水平（即y轴相等），可以设置V1=（0,1,0），V2=（0.5,1,0），计算的R旋转矩阵还是从V1向V2旋转，此时想将旋转后的点变换到旋转前，需要使用R的逆（这里旋转矩阵应该是正交矩阵，转置即为逆）

    旋转后的点=R*旋转前的点

    旋转前的点 = 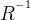R^{^{-1}}*旋转后的点

     预期效果：

    测试结果：

    1. p_out = []
    2. for p in p_arr:
    3.     tmp = R.I*np.matrix(p).T
    4.     p_out.append(tmp)

    最后贴一个根据两个向量计算它们之间的旋转矩阵 - 朔月の流光 - 博客园

    2022年9月1日add

    上面贴的链接图有误，加减号有问题。如下例子。

    1. Mat get_rot_matrix()
    2. {
    3.     Point3d norm_wall = Point3d(0, 1, 0);
    4.     Point3d norm_pro = Point3d(1, 0, 0);
    5.  
    6.     Point3d va = norm_wall / norm(norm_wall);
    7.     Point3d vb = norm_pro / norm(norm_pro);
    8.  
    9.     Point3d vs = va.cross(vb);
    10.     Point3d v = vs / norm(vs);
    11.     double ca = vb.dot(va);
    12.     Point3d vt = v * (1 - ca);
    13.     Mat rot = Mat::zeros(3, 3, CV_64FC1);
    14.  
    15.     rot.at<double>(0, 0) = vt.x * v.x + ca;
    16.     rot.at<double>(1, 1) = vt.y * v.y + ca;
    17.     rot.at<double>(2, 2) = vt.z * v.z + ca;
    18.  
    19.     vt.x *= v.y;
    20.     vt.z *= v.x;
    21.     vt.y *= v.z;
    22.  
    23.     rot.at<double>(0, 1) = vt.x - vs.z;
    24.     rot.at<double>(0, 2) = vt.z + vs.y;
    25.  
    26.     rot.at<double>(1, 0) = vt.x + vs.z;
    27.     rot.at<double>(1, 2) = vt.y - vs.x;
    28.  
    29.     rot.at<double>(2, 0) = vt.z - vs.y;
    30.     rot.at<double>(2, 1) = vt.y + vs.x;
    31.     cout << rot << endl;
    32.     return rot;
    33. }

    --end--

  • 相关阅读:
    不愧为清华大佬！只用30小时，就整理完成了这份JVM调优实战笔记
    GO语言篇之反射
    CVPR2022 | MPViT: Multi-Path Vision Transformer for Dense Prediction
    第13章、类继承
    什么是Spring Web MVC
    基于python的urllib 库抓取网站上的图片
    C++动态库调试技巧
    [操作系统] FIFO 与 LRU 替换算法一样的条件的重新表述
    VoLTE题库（含解析）-中高级必看
    在carla环境下使用BasicAgent进行导航
  • 原文地址：https://blog.csdn.net/cd_yourheart/article/details/126587124