机器学习实战（5）——支持向量机

目录

1 线性SVM分类

2 软间隔分类

3 非线性SVM分类

4 多项式核

5 添加相似特征

6 高斯RBF核函数

7 SVM回归

8 工作原理

8.1 决策函数和预测

8.2 训练目标

8.3 二次规划

8.4 对偶问题

8.5 核化SVM

---

支持向量机（简称SVM）是一个功能强大并且全面的机器学习模型，它能够执行线性或非线性分类、回归、甚至是异常值检测任务。SVM特别适用于中小型复杂数据集的分类。本篇博文中理论和理解的东西特别多。实在不懂的可以去哔哩哔哩找浙江大学胡浩基老师讲的支持向量机，简单易懂。（机器学习课程（六）支持向量机（线性模型）问题【720P】.qsv.flv_哔哩哔哩_bilibili）

1 线性SVM分类

上图所示的数据集来自鸢尾花数据集的一部分。左图显示了三种可能的线性分类器的决策边界。其中虚线所代表的的模型表现非常糟糕，甚至都无法正确实现分类其余两个模型在这个训练集上表现良好，但是他们的决策边界与实例过于接近，导致在面对新实例时，表现可能不太会好。相比之下，右图中的实现代表SVM分类器的决策边界，这条线不仅分离了两个类别，并且尽可能远离了最近的训练实例。我们可以将SVM分类器视为在类别之间拟合可能的最宽的街道（平行的虚线）。因此这也叫做大间隔分类。（位于街道边缘的实例称为支持向量）

大间隔分类代码演示：

常规模块的导入以及图像可视化的设置：

# Common imports
import numpy as np
import os
 
# to make this notebook's output stable across runs
np.random.seed(42) #结果复现
 
# To plot pretty figures #可视化
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

from sklearn.svm import SVC
from sklearn import datasets
 
iris = datasets.load_iris() #加载数据
X = iris["data"][:, (2, 3)]  # 花瓣长度和宽度
y = iris["target"]
 
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
 
# SVM Classifier model
svm_clf = SVC(kernel="linear", C=float("inf"))
svm_clf.fit(X, y)

# Bad models
x0 = np.linspace(0, 5.5, 200)
pred_1 = 5*x0 - 20
pred_2 = x0 - 1.8
pred_3 = 0.1 * x0 + 0.5
 
def plot_svc_decision_boundary(svm_clf, xmin, xmax):
    w = svm_clf.coef_[0]
    b = svm_clf.intercept_[0]
 
    # At the decision boundary, w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1
    x0 = np.linspace(xmin, xmax, 200)
    decision_boundary = -w[0]/w[1] * x0 - b/w[1]
 
    margin = 1/w[1]
    gutter_up = decision_boundary + margin
    gutter_down = decision_boundary - margin
 
    svs = svm_clf.support_vectors_
    plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
    plt.plot(x0, decision_boundary, "k-", linewidth=2)
    plt.plot(x0, gutter_up, "k--", linewidth=2)
    plt.plot(x0, gutter_down, "k--", linewidth=2)
 
plt.figure(figsize=(12,2.7))
 
plt.subplot(121)
plt.plot(x0, pred_1, "g--", linewidth=2)
plt.plot(x0, pred_2, "m-", linewidth=2)
plt.plot(x0, pred_3, "r-", linewidth=2)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 5.5, 0, 2])
 
plt.subplot(122)
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.xlabel("Petal length", fontsize=14)
plt.axis([0, 5.5, 0, 2])
 
plt.show()

运行结果如下：

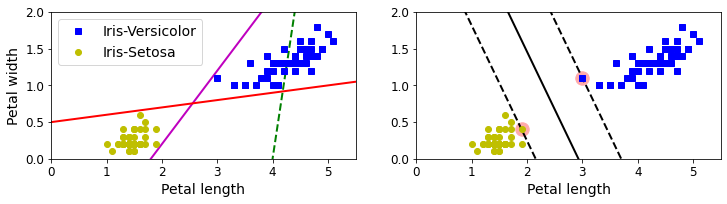
注意：SVM对特征缩放非常敏感，如下图，在左图中，垂直刻度比水平刻度大得多，因此可能的最宽的街道接近于水平。在特征缩放后，决策边界看起来好很多（右图）。

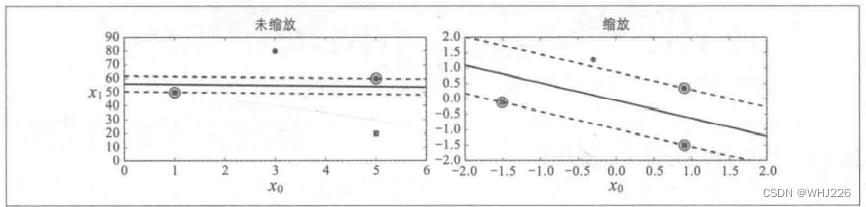
Xs = np.array([[1, 50], [5, 20], [3, 80], [5, 60]]).astype(np.float64)
ys = np.array([0, 0, 1, 1])
svm_clf = SVC(kernel="linear", C=100)
svm_clf.fit(Xs, ys)
 
plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(Xs[:, 0][ys==1], Xs[:, 1][ys==1], "bo")
plt.plot(Xs[:, 0][ys==0], Xs[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, 0, 6)
plt.xlabel("$x_0$", fontsize=20)
plt.ylabel("$x_1$  ", fontsize=20, rotation=0)
plt.title("Unscaled", fontsize=16)
plt.axis([0, 6, 0, 90])
 
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(Xs)
svm_clf.fit(X_scaled, ys)
 
plt.subplot(122)
plt.plot(X_scaled[:, 0][ys==1], X_scaled[:, 1][ys==1], "bo")
plt.plot(X_scaled[:, 0][ys==0], X_scaled[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, -2, 2)
plt.xlabel("$x_0$", fontsize=20)
plt.title("Scaled", fontsize=16)
plt.axis([-2, 2, -2, 2])

 运行结果如下：

2 软间隔分类

如果我们严格地让所有实例都不在街道上，并且位于正确的一边，这就是硬间隔分类。硬间隔分类有两个主要问题。首先，它只在数据是线性可分离的时候才有效；其次，它对异常值非常敏感。下图显示了有一个额外异常值的鸢尾花数据：左图的数据根本找不到硬间隔，而右图最终显示的决策边界与我们大间隔分类图中所看到的无异常值时的决策边界也大不相同，可能无法更好地泛化。

X_outliers = np.array([[3.4, 1.3], [3.2, 0.8]])
y_outliers = np.array([0, 0])
Xo1 = np.concatenate([X, X_outliers[:1]], axis=0)
yo1 = np.concatenate([y, y_outliers[:1]], axis=0)
Xo2 = np.concatenate([X, X_outliers[1:]], axis=0)
yo2 = np.concatenate([y, y_outliers[1:]], axis=0)
 
svm_clf2 = SVC(kernel="linear", C=10**9)
svm_clf2.fit(Xo2, yo2)
 
plt.figure(figsize=(12,2.7))
 
plt.subplot(121)
plt.plot(Xo1[:, 0][yo1==1], Xo1[:, 1][yo1==1], "bs")
plt.plot(Xo1[:, 0][yo1=&#