-
Android中的图像矩阵归一化
前言
在graphics包下的Matrix是一个3x3的矩阵,按网上的的图是这样的

MSCALE_X, MSCALE_Y表示缩放;
MSKEW_X, MSKEW_Y表示错切,与上面两个参数一起达到图像旋转效果;
MTRANS_X, MTRANS_Y表示平移;
MPERSP_0, MPERSP_1表示透视;
MPERSP_2固定为1。
在把图像矩阵应用到OpenGL中时遇到了问题:glsl中获取到的矩阵是归一化的,需要先把原来的矩阵进行归一化处理。
推导过程
按照矩阵乘法规则




如果考虑到透视变换,则最终的坐标X=x/z, Y=y/z;
设显示目标的尺寸为Tw,Th,归一化的坐标则是x1=X/Tw, y1=Y/Th;
 ............①
............① ............②
............②设图像原始宽高为w,h,归一化的矩阵为

那么,参照上面的等式,有


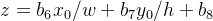
同样,考虑到透视变换,最终的归一化的坐标x1,y1为
 ............③
............③ ............④
............④①③联立并化简可得到
上式的每一项均为0,才能保证结果一定为0,因此有
 (1)
(1)  (2)
(2)  (3)
(3)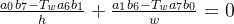 (4)
(4) (5)
(5) (6)
(6)同理,②④联立可得
 (7)
(7)  (8)
(8)  (9)
(9)理论上(1)-(9)共9个方程,b0-b8共9个未知数,可以解方程,但其实a8=b8=1,所以上述方程组可以化简,最终结果是

有兴趣的朋友可以推导验证一下。
代码实现
- /**
- * 图像缩放矩阵归一化
- *
- * @param src 图像裁剪及缩放矩阵,length=9
- * @param width 图像原宽度
- * @param height 图像原高度
- * @param targetWidth 目标图像宽度,即显示的图像宽度,如100像素的宽度拉伸显示在300像素的View中,则应为100
- * @param targetHeight 目标图像高度,即显示的图像高度
- */
- public static float[] normalize(float[] src, int width, int height, int targetWidth, int targetHeight) {
- float[] values = new float[9];
- values[Matrix.MSCALE_X] = src[0] * width / targetWidth;
- values[Matrix.MSKEW_X] = src[1] * height / targetWidth;
- values[Matrix.MTRANS_X] = src[2] / targetWidth;
- values[Matrix.MSKEW_Y] = src[3] * width / targetHeight;
- values[Matrix.MSCALE_Y] = src[4] * height / targetHeight;
- values[Matrix.MTRANS_Y] = src[5] / targetHeight;
- values[Matrix.MPERSP_0] = src[6] * width;
- values[Matrix.MPERSP_1] = src[7] * height;
- values[Matrix.MPERSP_2] = src[8];
- return values;
- }
-
相关阅读:
极客范儿的浏览器主页YuIndex
Mybatis学习笔记-映射文件,标签,插件
关于对随机森林接口predict_proba()的个人理解
ES聚合统计
深度学习笔记_2、多种方法定义神经网络
C#WPF控件Button详解
成都榆熙:转化率的定义是什么?如何提升?
解决hive表新增的字段查询为空null问题
文件的逻辑结构与物理结构的对比与区别
生产依赖与开发依赖区别: 前端程序没有区别,后端程序有点区别
- 原文地址:https://blog.csdn.net/wlxyhy/article/details/126555104
