提示学习用于推荐系统问题（PPR，PFRec）

前一篇整理过一些Prompt和推荐系统结合的文章，并取得了一些很不错的效果。博主以往的博文中更过一期预训练和自监督用于推荐系统系列的文章，特别是随着预训练技术在推荐系统模型中也逐步被验证有效，那么过渡到prompt-based模式借助更多的预训练知识也很自然，尤其是在冷启动等问题上。

• 提示学习用于推荐系统问题（PEPLER，P5，PRL）

最近相关领域又新出了一些文章，本篇博文继续更新。关于更多prompt learning的基础技术和相关应用，博主已经在很多文章中都已经整理，不做赘述。

• 预训练新范式（Prompt-tuning，Prefix-tuning，P-tuning）
• 多模态预训练中的Prompt（MAnTiS，ActionCLIP，CPT，CoOp）
• 多模态预训练中的Prompt（ALPRO，Frozen）
• 对比学习用于推荐系统问题（SSL，S^3-Rec，SGL，DHCN，SEMI，MMCLR）
• 自监督学习用于推荐系统问题综述

---

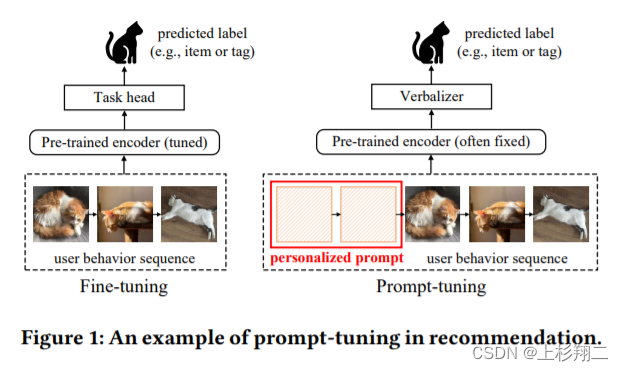
Personalized Prompts for Sequential Recommendation
用于个性化提示学习的序列推荐。在这项工作中，作者针对冷启动推荐提出了一种新的个性化基于提示的推荐（PPR）框架。作者认为主要面临的困难将是：

• （1）如何将prompt从nlp领域应用到推荐领域？ 与 NLP 中的单词不同，推荐中的行为（即item）很难直接用于构建难以解释的提示和标签。 此外，设计一个合适的框架以充分利用预训练知识进行个性化推荐也具有挑战性。
• （2）如何为个性化推荐构建合适的提示？ 与 NLP 相比，推荐更看重个性化。 因此，prompt的提示应该更好地个性化，以便从庞大的预训练模型中更针对性地提取用户相关知识。

具体来说，作者主要是提出了一种personalized soft prefix prompt，通过基于用户配置文件的提示生成器构建个性化的软预提示，再通过基于提示和基于行为的增强的面向提示的对比学习实现对提示的充分训练。

模型结构如下，首先由一个预训练过的序列模型（SASRec）作为基模型。

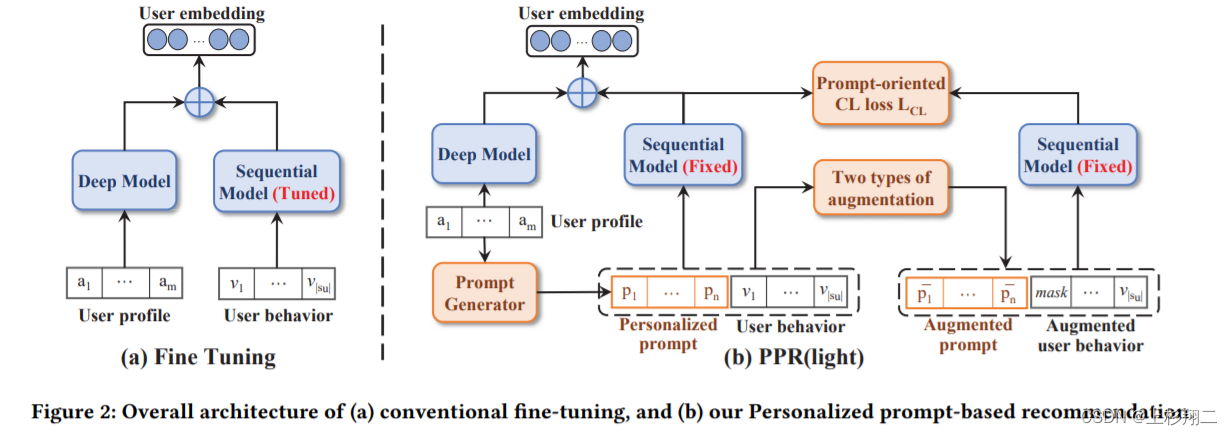
• 个性化提示生成。提示生成器根据用户档案（如用户静态属性，如年龄、性别）构建个性化提示，并将它们插入到用户的开头行为序列。$$x_u=[a_1^u||a_2^u||...||a_m^u]$$$$p^u=PPG(x_u|\theta )=W_2\sigma (W_1{x}_u+b_1)+b_2$$
• 用户表示。然后将新序列输入到预训练好的序列模型中，以获取用户的行为偏好。同时会将用户画像进一步添加到另一个网络中生成用户的属性偏好，以补充冷启动用户信息，以得到最终的用户表示。
• 对比学习损失。在 PPR中，预训练模型在提示调整期间是固定的，即图中的fixed。但为了对个性化提示进行更充分的训练，作者在 PPR 中进一步设计了一组对比学习损失，在提示生成器和序列建模部分采用数据增强。两者分别对用户配置和行为数据进行随机掩码，然后计算对比损失。
  $$L_{CL}=-\sum _{u\in U^c}log\frac{exp(sim(u_s,u_s^{\prime })/\tau )}{exp(sim(u_s,u_s^{\prime })+{\sum }_{u^{\prime }\in S_{-}^u}exp(sim(u_s,u_s^{\prime }))}$$

http://arxiv.org/abs/2205.09666v1

Selective fairness in recommendation via prompts
来自SIGIR22，文章主要探讨的方向是：用户自选公平性（selective fairness），即用户可以灵活地选择哪些用户属性应当被推荐系统所考虑，使得推荐结果在这些属性上保持公平。例如，在音乐推荐中，推荐系统可以根据年龄给用户推荐这个时代的人喜欢的音乐，但如果用户希望跳出自己年龄的信息茧房的话，就需要给用户提供一个关于属性的公平性选择开关（如年龄），这样用户就可以主要选择哪些个人属性会被考虑/不考虑。主要有两大挑战 ：

• 属性组合数n随着用户属性数m的增加呈指数型增加。但现有大多数公平性模型对每一种属性组合都训练一个单独的模型，这是非常低效甚至是不可能的。
• 数据稀疏性。稀疏性将在用户特定了属性组合后更稀疏。因此，用户可选公平模型应充分利用未去偏的用户历史行为信息，在满足公平性时保证推荐准确性。

于是作者们提出了基于prompt的用户自选公平模型（PFRec)，模型图如下：

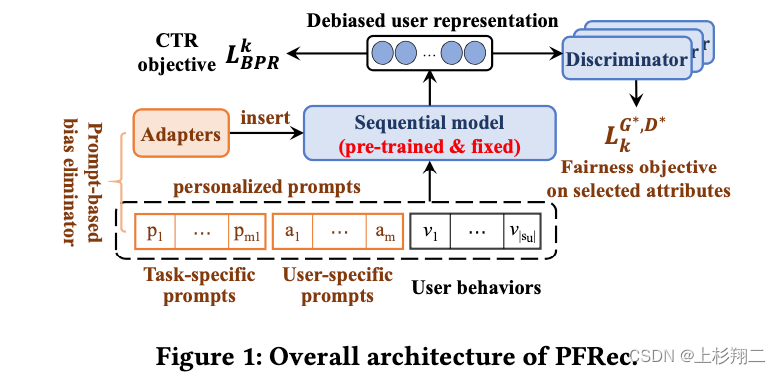
基于对抗生成网络来实现去偏，主要有以下几个阶段：

• 预训练。首先作者基于所有的用户历史数据训练一个序列化推荐模型作为预训练模型（如BERT4Rec, SASRec等），值得注意的是这个模型并没有任何公平性考量，是作为后续微调的基模型。
• 生成器（偏差消除器bias eliminators）。针对motivation的第一个属性组合数量多的问题，生成器的目标是根据用户的需求尽可能地生成公平的用户向量，同时让推荐的结果更加准确。如上图，生成器主要有两部分，prompt和adapter。
  1）personalized attribute-specific prompt：其中task-specific prompt根据用户需要生成不同属性组合m种偏差消除器，user-specific prompt通过用户的个性化属性生成。这些prompt会拼接到用户历史行为序列前作为prefix prompt，来生成新的序列。 s u k = { p t k , p u , v 1 u , v 2 u , . . . , v ∣ s u ∣ u } s^k_u=\{p^k_t,p_u,v^u_1,v^u_2,...,v^u_{|s_u|}\} suk​={ptk​,pu​,v1u​,v2u​,...,v∣su​∣u​}2）adapter：作为prompt的辅助，最后prompt-enhanced的用户行为序列被送入到预训练模型中，输出我们认为在用户选择属性上保持公平的用户向量：$$u^k=f_{seq}(s_u^k|\Theta ,{\theta }^k)=h_{u,m_1+m+|s_u|}^{L,k}$$其中在prompt-tuning阶段只有偏差消除器的参数被更新，而预训练模型则被固定。
• 判别器。判别器的作用是用来判断经过偏差消除器后的用户表示是否足够公平。即实现一个分类，如果一个偏差消除器生成的用户向量无法被判别器准确猜测出用户向量对应的属性，则此向量可以被认为在这种用户属性上具有公平性。
  $$L_k^{G^{\ast },D^{\ast }}=\underset{{\varphi }^k}{\min }\underset{{\theta }^k}{\max }\sum _B\sum _{u\in B}\sum _{a_i\in Q_k}-E_{u^k}[log(P(a_i|u^k,{\varphi }^k))]$$

paper：https://arxiv.org/abs/2205.04682
code：https://github.com/wyqing20/PFRec