662. 二叉树最大宽度（难度：中等）

662. 二叉树最大宽度（难度：中等）

题目链接：https://leetcode.cn/problems/maximum-width-of-binary-tree/

题目描述：

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。
1
2
3

示例 2：

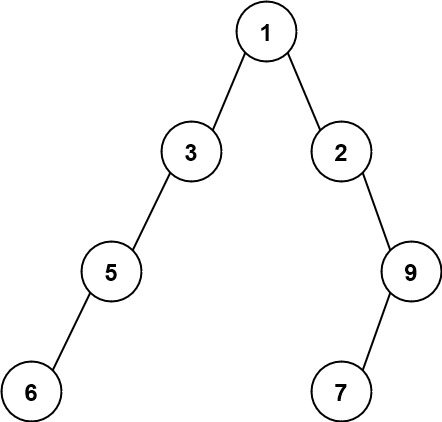
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。
1
2
3

示例 3：

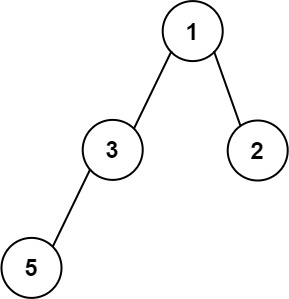
输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。
1
2
3

解法：广度优先搜索

我们利用广度优先遍历，实现层序遍历，遍历每层时，给每一个的元素进行编号。

编号规则：

元素i的序号为n，则他的左子树结点的序号为2 * n，右子树的序号为2 * n + 1，

根据这个规则，我们计算每层宽度，只需要拿到每层的最小序号 min 和最大序号max，每层的宽度为max - min + 1。

我们可以利用Map来存放每个节点与序号之间的关系。

注意：这道题有个边界问题，Integer的作用域不够，需要把记录序号的类型用Long。

代码如下：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        Deque<TreeNode> queue = new ArrayDeque<>();
        Map<TreeNode,Long> map = new HashMap<>();
        long result = 0;
        if(root == null) {
            return 0;
        }
        queue.offer(root);
        map.put(root,0L);
        result = 1;

        while (!queue.isEmpty()) {
            long min = Long.MAX_VALUE;
            long max = Long.MIN_VALUE;
            int s = queue.size();
            for(int i = 0;i<s;i++) {
                TreeNode poll = queue.poll();
                Long val = map.get(poll);
                min = Math.min(min,val);
                max = Math.max(max,val);
                if(poll.left!= null) {
                    map.put(poll.left,val * 2);
                    queue.offer(poll.left);
                }
                if(poll.right!= null) {
                    map.put(poll.right,val * 2 + 1);
                    queue.offer(poll.right);
                }
            }
            result = Math.max(result,max - min + 1);
        }
        return (int)result;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50